GCN
GCN的目的
将神经网络应用与图结构.
从原始图获取每个顶点的特征嵌入feature embedding.
特征嵌入的特点:
- 低维: 维度数小于节点个数(优于
one-hot embedding) - 连续: 每个元素为连续实数.
- 稠密: 大部分元素不为0.
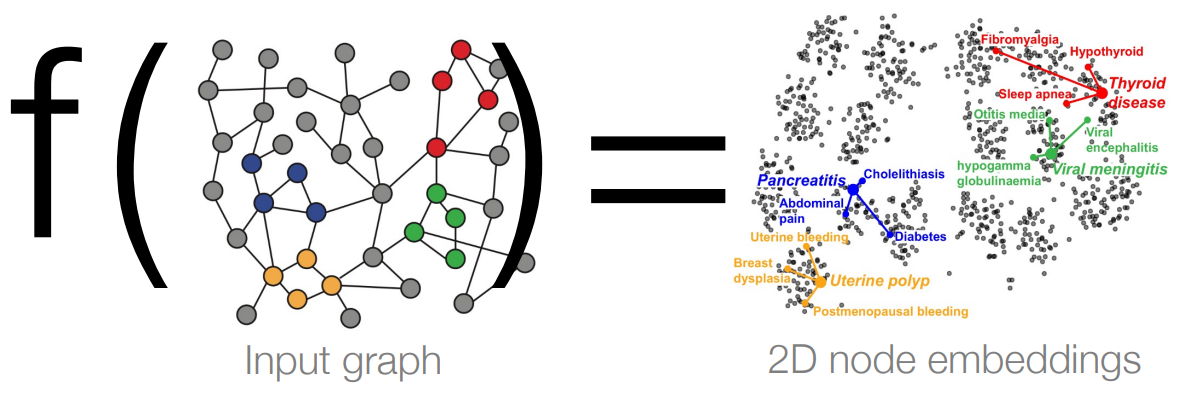
\(d\)维的嵌入距离接近的顶点具有相近的关系(类似词嵌入表示). 有了feature embedding, 便于后续的任务处理.
GCN的计算过程
消息传递
Design GCN that are permutation invariant / equivariant by passing and aggregating information from neighbors.
通过汇聚(Pooling, 可以通过Max, Avg, Sum等具有交换律的计算方法)与节点\(u\)相邻节点的信息, 得到该节点的嵌入表示.
聚合相邻点的信息过程称为卷积 -- 图片Image也可以看成一个特殊的图, 不同之处在于GCN的卷积过程需要考虑不同的图结构(由邻接矩阵\(A\)表示).
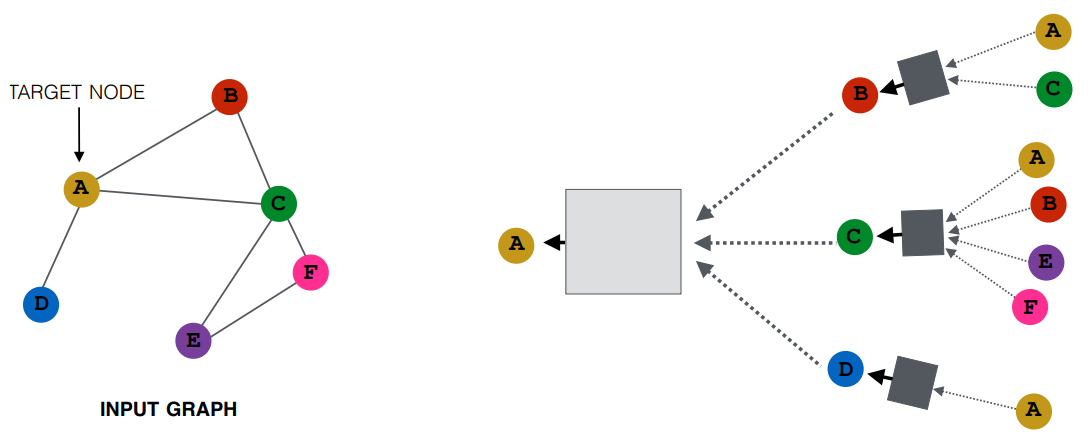
GCN的层layer
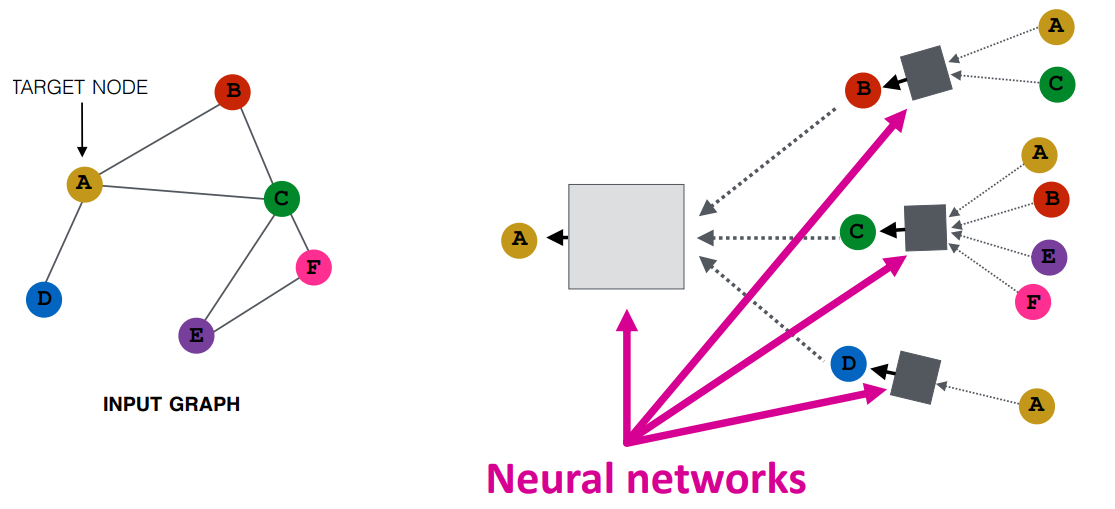
汇聚相邻节点信息后,可以通过神经网络进一步处理,图中每一个矩形框代表NN网络,
且相同颜色的矩形框代表的网络的参数共享. 对于GCN来说,其层数是计算图中不同颜色
矩形框的个数.
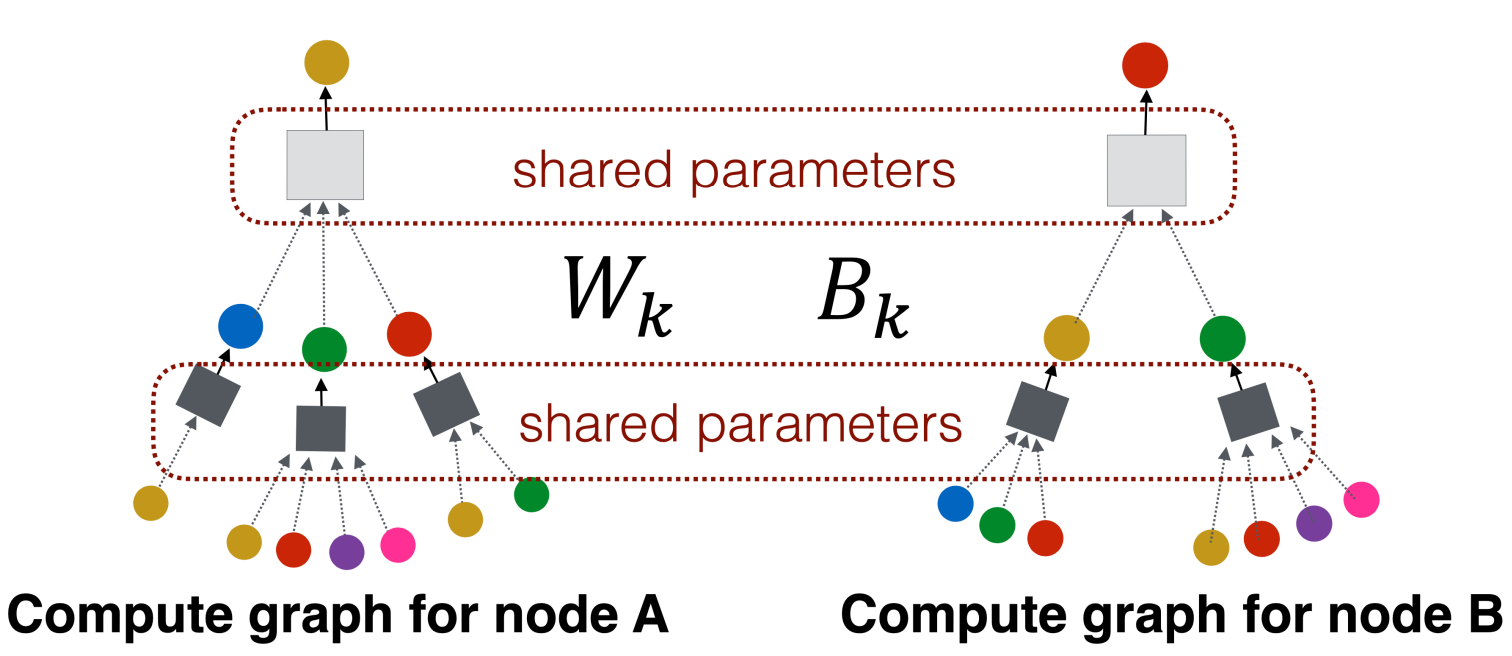
对于一层的GCN, 每个节点接受其相邻节点信息; 对于二层GCN, 每个节点接受与其距离小于\(2\)的节点信息:
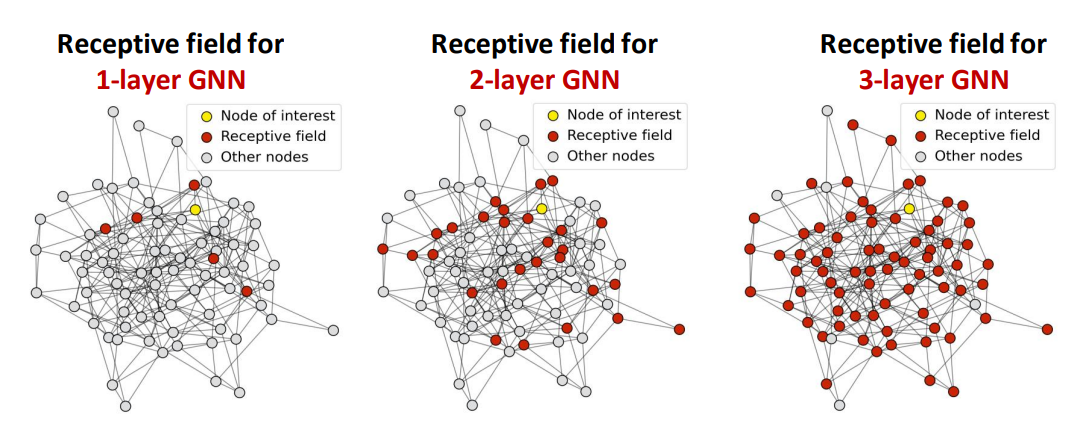
数学形式
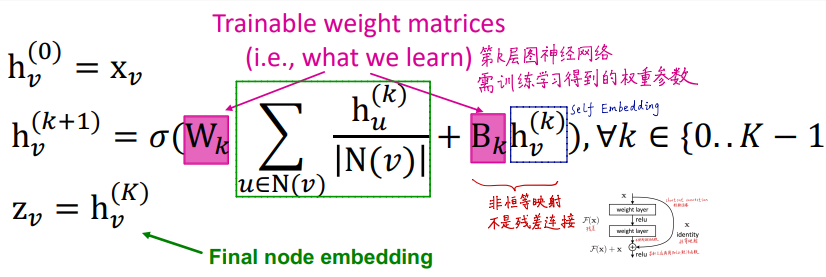
对于第一层,汇聚每个顶点的初始信息,接着进入NN网络作为该节点信息; 迭代汇聚过程.
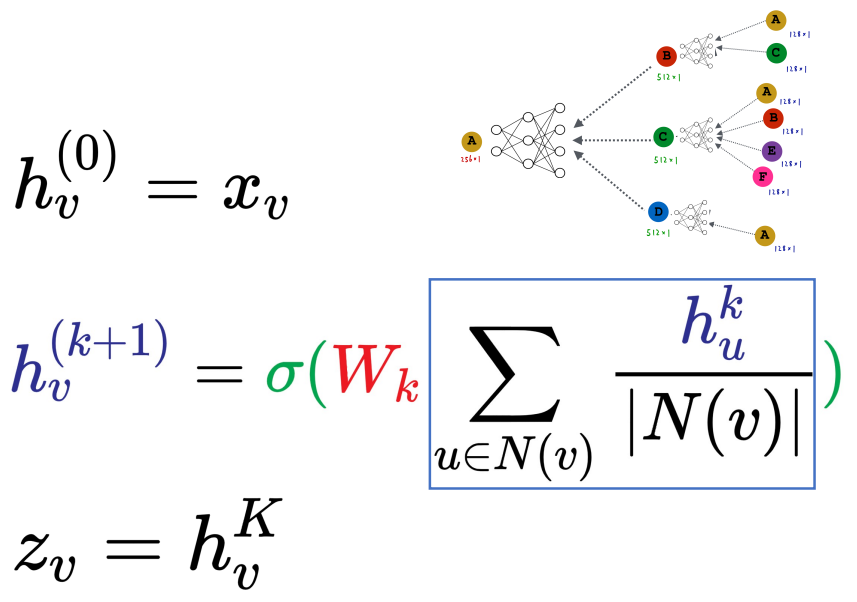
其中\(W_k\)是可学习的trainable投影矩阵(MLP), \(\sigma\)表示激活函数.
也可以用矩阵形式简洁表示:
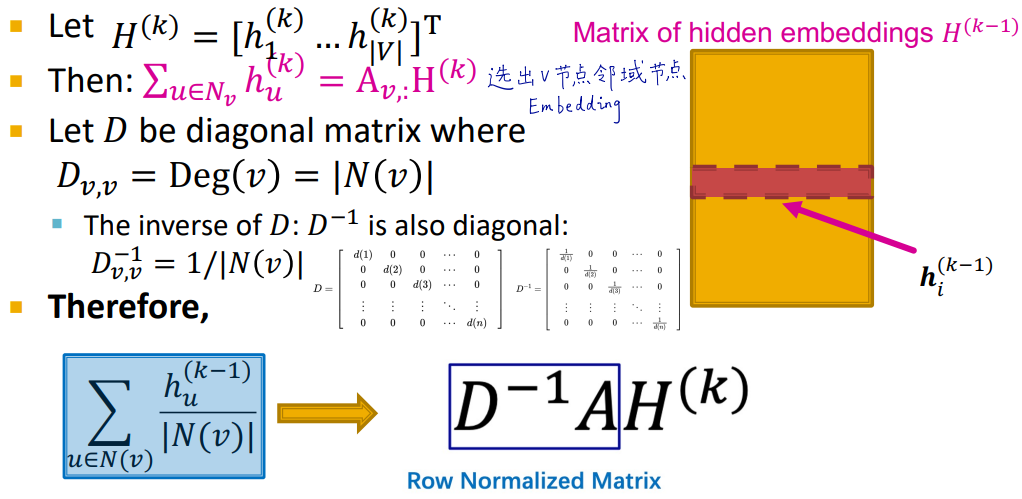
我们把顶点嵌入concat为一个矩阵\(H\in R^{V\times d}\), \(V\)行, 每行表示一个顶点的嵌入表示.
对于顶点\(v\), 其邻接矩阵对应的行\(A_v\in R^{1\times V}\)表示与其相连的顶点.
\(A_v H\)即表示使用Sum操作汇聚与节点\(v\)相邻节点的信息.
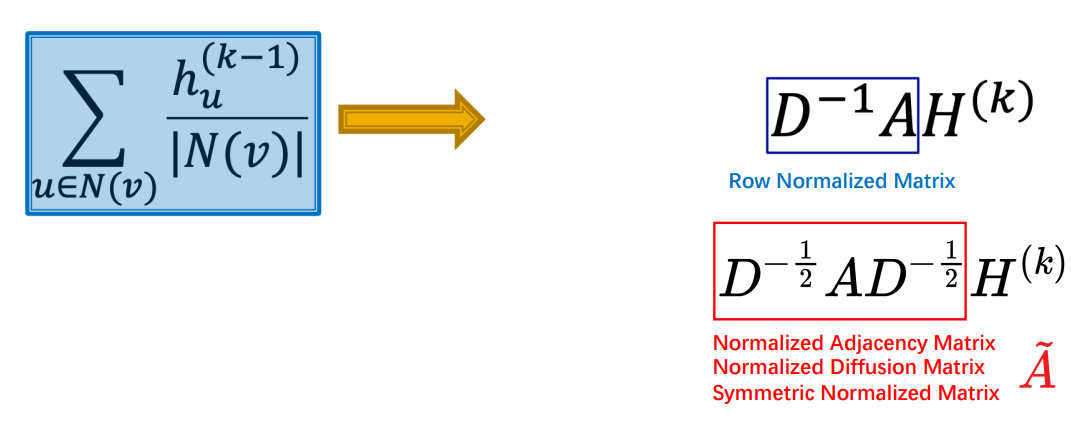
再通过表示每个节点度degree倒数的矩阵\(D^{-1}\), 得到汇聚信息的平均值.
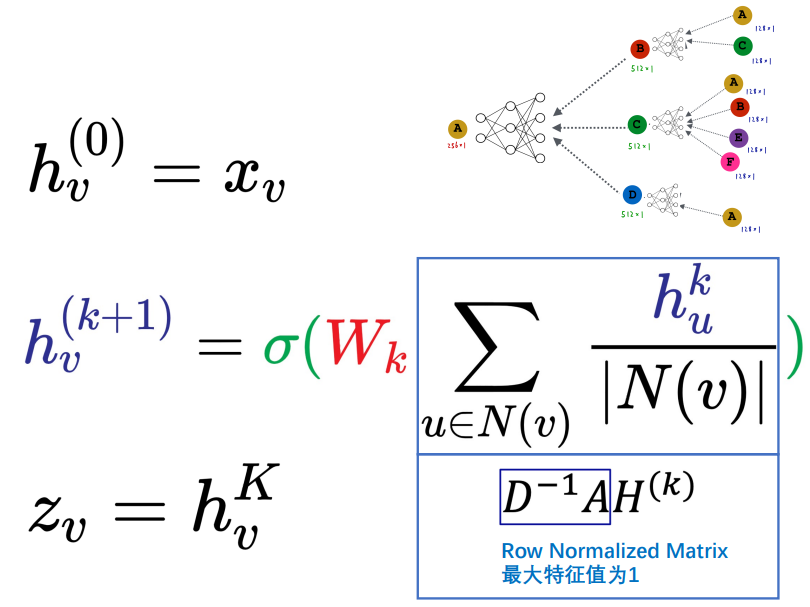
考虑\((u, v)\)各自的度
此时顶点\(v\)只考虑了自身的度, 与其相邻的顶点\(u\)可能只与\(v\)相连, 也可能与很多顶点相连.
将\(v\)、\(u\)的度同时考虑, 我们可以进一步右乘\(D^{-1}\): \(D^{-1}AD^{-1}H\)
但此时\(D^{-1}AD^{-1}\)的特征值在\(-1\)到\(1\)之间, 我们知道\(A\vec{v} = \lambda \vec{v}\), 经过
多次相乘, \(H\)的赋值会发生变化. 为保证特征值为一, 我们使用公式\(D^{-1/2}AD^{-1/2}H\).
考虑自身inner voice / self-embedding
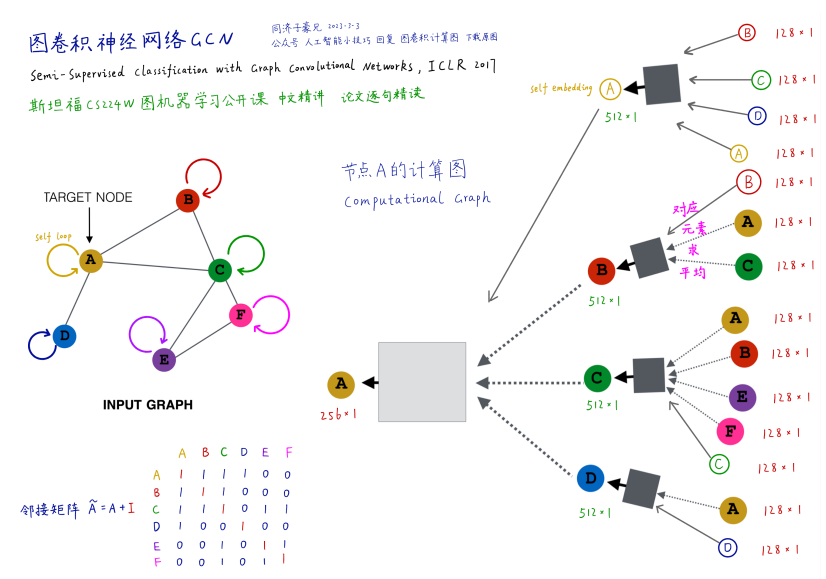
体现在公式中, 就是邻接矩阵\(A\)加上单位矩阵\(I\), 即考虑\(v\rightarrow v\)的情况: \(\tilde{A} = A + I\), \(H^{k+1} = \sigma(D^{-1/2} \tilde{A} D^{-1/2} H^{k})\)
进一步, 我们还可以给相连节点与自身两个不同的投影矩阵(NN网络):

GCN代码
def normalization(adjacency):
"""
D^(-1/2) (A+I) D^(-1/2)
"""
adjacency += sp.eye(adjacency.shape[0])
degree = np.array(adjacency.sum(1))
d_hat = sp.diags(np.power(degree, -0.5).flatten())
return d_hat.dot(adjacency).dot(d_hat).tocoo()
class GraphConvolution(nn.Module):
def __init__(self, input_dim, output_dim, use_bias=True):
"""
图卷积 A H W
"""
super(GraphConvolution, self).__init__()
self.input_dim = input_dim
self.output_dim = output_dim
self.use_bias = use_bias
self.weight = nn.Parameter(torch.Tensor(input_dim, output_dim))
if self.use_bias:
self.bias = nn.Parameter(torch.Tensor(output_dim))
else:
self.register_parameter('bias', None)
self.reset_parameters()
def reset_parameters(self):
init.kaiming_uniform_(self.weight)
if self.use_bias:
init.zeros_(self.bias)
def forward(self, adjancency, input_feature):
"""
邻接矩阵是稀疏矩阵, 在计算时使用稀疏矩阵乘法
"""
# H W
support = torch.mm(input_feature, self.weight)
# A (H W)
output = torch.sparse.mm(adjancency, support)
if self.use_bias:
output += self.bias
return output
class GCNNet(nn.Module):
"""
包含两层图卷积GraphConvolution的网络
"""
def __init__(self, input_dim=1433, hidden_dim=16, output_dim=7):
super(GCNNet, self).__init__()
self.gcn1 = GraphConvolution(input_dim, hidden_dim)
self.gcn2 = GraphConvolution(hidden_dim, output_dim)
def forward(self, adjacency, feature):
h = F.relu(self.gcn1(adjacency, feature))
h = self.gcn2(adjacency, feature)
return h


 浙公网安备 33010602011771号
浙公网安备 33010602011771号