蓝桥杯 试题 历届试题 危险系数 并查集/dfs

问题描述

抗日战争时期，冀中平原的地道战曾发挥重要作用。

地道的多个站点间有通道连接，形成了庞大的网络。但也有隐患，当敌人发现了某个站点后，其它站点间可能因此会失去联系。

我们来定义一个危险系数DF(x,y)：

对于两个站点x和y (x != y), 如果能找到一个站点z，当z被敌人破坏后，x和y不连通，那么我们称z为关于x,y的关键点。相应的，对于任意一对站点x和y，危险系数DF(x,y)就表示为这两点之间的关键点个数。

本题的任务是：已知网络结构，求两站点之间的危险系数。

输入格式

输入数据第一行包含2个整数n(2 <= n <= 1000), m(0 <= m <= 2000),分别代表站点数，通道数；

接下来m行，每行两个整数 u,v (1 <= u, v <= n; u != v)代表一条通道；

最后1行，两个数u,v，代表询问两点之间的危险系数DF(u, v)。

输出格式

一个整数，如果询问的两点不连通则输出-1.

样例输入

7 6
1 3
2 3
3 4
3 5
4 5
5 6
1 6

样例输出

2

---

解题思路：

• 题目即求割点。因为并查集可以判断两点是否联通(类似于蓝桥杯发现环:https://www.cnblogs.com/w-like-code/p/12934398.html)，所以一个思路是依次去掉通道，判断此时u,v是否联通，

若不联通说明与此边的点为关键点。注意让避免重复计算某点，且要排除u,v。

• 实现代码:

#include<cstdio>

const int Max_N = 1000;
const int Max_M = 2000;

int n,m;
int U[Max_M],V[Max_M]; //保存通道两点 
int u,v; //待查询 

int par[Max_N+1];
int rank[Max_N+1];

bool used[Max_N+1];

void init( int n )
{
    for( int i=1; i<=n; i++ )
    {
        par[i] = i;
        rank[i] = 0;
    }
}

int find( int x )
{
    if( par[x]==x ){
        return x;
    }
    return par[x] = find( par[x] );
}

void unite( int x, int y)
{
    x = find(x); y = find(y);
    if( x==y ){
        return;
    }
    if( rank[x]<rank[y] ){
        par[x] = y;
    }
    else{
        par[y] = x;
        if( rank[x]==rank[y] ){
            rank[x]++;
        }
    }
}

bool same( int x, int y )
{
    return find(x)==find(y);
}

void solve()
{
    //首先判断u,v是否联通  
    init( n );
    for( int i=0; i<m; i++ ){
        unite( U[i],V[i] );
    }
    if( !same(u,v) ){  
        printf("-1\n");
        return;
    }
    
    //每次判处下标为i的通道 用并查集判断关键点 
    int res = 0;
    for( int i=0; i<m; i++ )
    {
        init(n);
        for( int j=0; j<m; j++ )
        {
            if( i==j )    continue;
            
            unite(U[j],V[j]);
        }
        if( !same(u,v) ){
            if( !used[U[i]] ){ //用used[]避免重复计算 
                res++;
                used[U[i]] = true;
            }
            if( !used[V[i]] ){
                res++;
                used[V[i]] = true;
            }
        }
    }
    if( used[u] )    res--;
    if( used[v] )    res--;
    
    printf("%d\n",res);
}

int main()
{
    scanf("%d%d",&n,&m);
    for( int i=0; i<m; i++ )
    {
        scanf("%d%d",&U[i],&V[i]);
    }
    scanf("%d%d",&u,&v);
    
    solve();
    
    return 0;
}

• 另一个思路是用dfs判断从u到v的所有路径，而关键点就是每个u到v路径都要经过的点。
• 实现代码: 首先思路是若dfs到达v，返回true,所有返回true的节点都+1。但可能出现:
• 

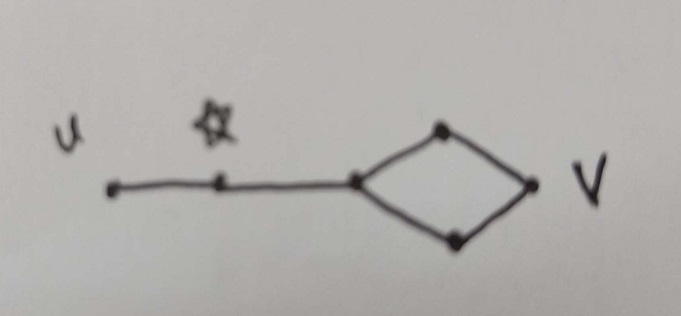
• 对于五角星割点,其只有一次返回true,计数为1，但实际上u-v路径数为2

• 错误代码: 

#include<cstdio>
#include<vector>
using namespace std;

const int Max_N = 1000;
const int Max_M = 2000;

//输入 
int n,m;
int u,v;
vector<int> G[Max_N+1]; //图

bool visited[Max_N+1]; //visited[i]:在当前dfs()中是否访问过i 
int count[Max_N+1]; //count[i]:下标i出现在u-v路径中的次数 
int sum; //计算所有路径数 
 
bool dfs( int x )
{
    if( x==v ){
        sum++;
        return true;
    }
    
    bool flag = false;
    for( int i=0; i<G[x].size(); i++ )
    {
        int x_ = G[x][i];
        if( !visited[x_] )
        {
            visited[x_] = true;
            if( dfs( x_ ) ){
                count[x]++;
                flag = true;
            }
            visited[x_] = false;    
        } 
    }
    return flag;
}

void solve()
{    
    
    visited[u] = true;
    if( !dfs( u ) ){//若u,v不连通 
        printf("-1\n");
        return;
    }
    
    int res = 0;
    for( int i=1; i<=n; i++ )
    {
        if( count[i]==sum ){
            res++;
        }
    }
    
    if( count[u]==sum )    res--;//多记录了u 
    
    printf("%d\n",res); 
}

int main()
{
    scanf("%d%d",&n,&m);
    for( int i=0; i<m; i++ )
    {
        int x,y;
        scanf("%d%d",&x,&y);
        G[x].push_back(y); G[y].push_back(x);
    }
    scanf("%d%d",&u,&v);
    
    solve();
    
    return 0;
}

• 只要用一个数组将经过节点保存,并记录数组长度，当到达v时把数组中节点计数即可。
• 正确代码:

#include<cstdio>
#include<vector>
using namespace std;

const int Max_N = 1000;
const int Max_M = 2000;

//输入 
int n,m;
int u,v;
vector<int> G[Max_N+1]; //图

bool visited[Max_N+1]; //visited[i]:在当前dfs()中是否访问过i 
int count[Max_N+1]; //count[i]:下标i出现在u-v路径中的次数 
int sum; //计算所有路径数 

int way[Max_N]; //记录路径节点 
 
void dfs( int x , int index )
{
    if( x==v ){
        sum++;
        for( int i=0; i<index; i++ ){
            count[way[i]]++;
        }
        return;
    }
    
    way[index] = x;
    for( int i=0; i<G[x].size(); i++ )
    {
        int x_ = G[x][i];
        if( !visited[x_] )
        {
            visited[x_] = true;
            dfs( x_, index+1 );
            visited[x_] = false;    
        } 
    }
}

void solve()
{    
    
    visited[u] = true;
    dfs( u , 0 );
    
    if( count[u]==0 ){
        printf("-1\n");
        return;
    }
    
    int res = 0;
    for( int i=1; i<=n; i++ )
    {
        if( count[i]==sum ){
            res++;
        }
    }
    
    printf("%d\n",res-1); //多记录了节点u 
}

int main()
{
    scanf("%d%d",&n,&m);
    for( int i=0; i<m; i++ )
    {
        int x,y;
        scanf("%d%d",&x,&y);
        G[x].push_back(y); G[y].push_back(x);
    }
    scanf("%d%d",&u,&v);
    
    solve();
    
    return 0;
}