整数二进制展开中数位1的总数
前言
目前在,额,怎么说呢,回炉重造数据结构,今天在邓俊辉老师的书上看到了一个很有意思的算法,第一遍没看明白,后面仔细想了一下才搞明白什么意思,觉得很有趣,记录一下。
这个算法如题所言,统计整数二进制展开中数位1的总数
,网上常见的算法是通过将数n二进制展开中的最低位1转置0来统计,此算法本文也会介绍(说是介绍其实是抄书啦),然邓老师书上又介绍了一个更有趣的算法,这个会介绍本人的见解。
设输入一个数n,位宽W=log n.
1.第一种算法
先上代码
0001 int countOnes1 ( unsigned int n ) { //统计整数二进制展开中数位1的总数:O(ones)正比于数位1的总数
0002 int ones = 0; //计数器复位
0003 while ( 0 < n ) { //在n缩减至0之前,反复地
0004 ones++; //计数(至少有一位为1)
0005 n &= n - 1; //清除当前最靠右的1
0006 }
0007 return ones; //返回计数
0008 } //等效于glibc的内置函数int __builtin_popcount (unsigned int n)
对这个算法的理解就是对于任意整数n,设最低数位1对应于2^k,于是n的二进制展开
1后面有k个0;
n-1 的二进制展开
n&(n-1)的结果:
n的二进制展开
后面K+1位全都变成了0,成功消除了最低位的1.如此,最低位的1会依次被消除,循环次数正是1的个数。
这个算法的复杂度正比于1的个数,O(1的个数);最坏情况O(log n)=O(W),线性正比于n的二进制位宽。
2.第二种算法
也是先上代码
.
0001 #define POW(c) (1 << (c)) //2^c
0002 #define MASK(c) (((unsigned long) -1) / (POW(POW(c)) + 1)) //以2^c位为单位分组,相间地全0和全1
0003 // MASK(0) = 55555555(h) = 01010101010101010101010101010101(b)
0004 // MASK(1) = 33333333(h) = 00110011001100110011001100110011(b)
0005 // MASK(2) = 0f0f0f0f(h) = 00001111000011110000111100001111(b)
0006 // MASK(3) = 00ff00ff(h) = 00000000111111110000000011111111(b)
0007 // MASK(4) = 0000ffff(h) = 00000000000000001111111111111111(b)
0008
0009 //输入:n的二进制展开中,以2^c位为单位分组,各组数值已经分别等于原先这2^c位中1的数目
0010 #define ROUND(n, c) (((n) & MASK(c)) + ((n) >> POW(c) & MASK(c))) //运算优先级:先右移,再位与
0011 //过程:以2^c位为单位分组,相邻的组两两捉对累加,累加值用原2^(c + 1)位就地记录
0012 //输出:n的二进制展开中,以2^(c + 1)位为单位分组,各组数值已经分别等于原先这2^(c + 1)位中1的数目
0013
0014 int countOnes2 ( unsigned int n ) { //统计整数n的二进制展开中数位1的总数
0015 n = ROUND ( n, 0 ); //以02位为单位分组,各组内前01位与后01位累加,得到原先这02位中1的数目
0016 n = ROUND ( n, 1 ); //以04位为单位分组,各组内前02位与后02位累加,得到原先这04位中1的数目
0017 n = ROUND ( n, 2 ); //以08位为单位分组,各组内前04位与后04位累加,得到原先这08位中1的数目
0018 n = ROUND ( n, 3 ); //以16位为单位分组,各组内前08位与后08位累加,得到原先这16位中1的数目
0019 n = ROUND ( n, 4 ); //以32位为单位分组,各组内前16位与后16位累加,得到原先这32位中1的数目
0020 return n; //返回统计结果
0021 } //32位字长时,O(log_2(32)) = O(5) = O(1)
POW(C)和MASK(C),这个很简单,大家应该看得懂,我用表格列一下,大家可以有更直观地感受
| c | POW(C) | POW(POW(C)) | POW(POW(C))+1 |
|---|---|---|---|
| 0 | 1 | 2 | 3 |
| 1 | 2 | 4 | 5 |
| 2 | 4 | 16 | 17 |
| 3 | 8 | 256 | 257 |
| 4 | 16 | 65536 | 65537 |
其中((unsigned long) -1)就是32位1,MASK(c)就这样得到了如注释所示的几个的数字,很神奇啊!
ROUND函数中对MASK数的利用是整个算法的精髓与奥妙所在。
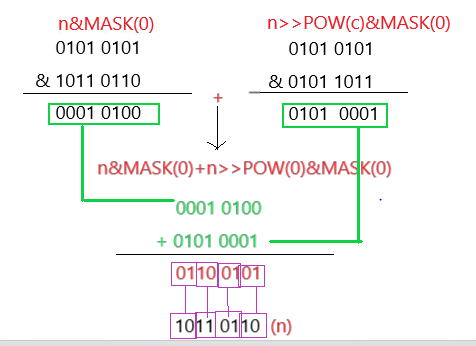
先看(n) & MASK(0),鉴于32位太长我们以8位为例,n取(1011 0110)(初始值);此时c取到2就够了;MASK(c)我们也用不到32位,同样取8位,如图1 所示:
图1 :
与常见的M位二进制存一个数的思维不同,此时的n看做8个一位二进制数存了8个数,一位二进制数取值范围就是0-1。这一步相当于相邻2个一位数相加得到1个两位的二进制数;8个一位数相邻两个相加总共得到4个两位的二进制数,如上图中下方的4个紫色的小方框。
那这两位的二进制数代表什么意思呢?结合上面的分析和图2,不难看出,最终求出的和 0110 0101 看做4个两位的二进制数后,其实记录的就是输入的n对应的相邻两位二进制数中相邻两位数中1的个数。例如最高的两位n中有1个1 对应结果中最高二位01 (十进制1),次高二位2个1对应结果中次高二位 10 (十进制2),依次类推
图2:
当c=1时,n更新为上面计算出的结果 0110 0101,过程如下图所示,不再赘述。
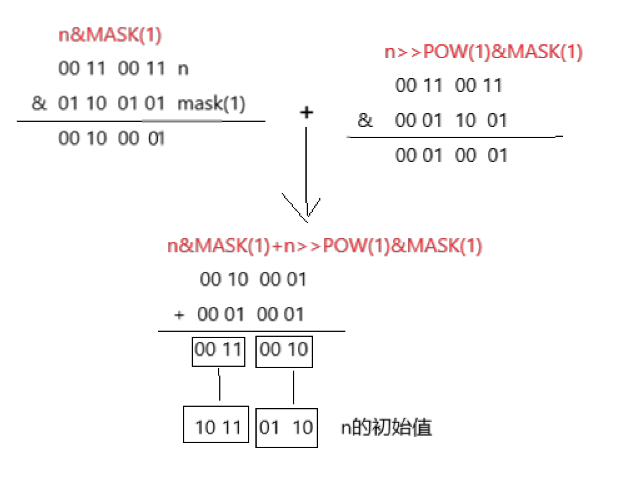
n更新为 0011 0010,结果高4位记录着n初值高4位有几个1;低四位同理。
最后一步 0011 + 0010 =0101,也就是n初值中有5个1.
复杂度 为O(log W),开头我们说的很明白,W=log n.此时,复杂度也可写为O(log(logn)),这是个低到发指的复杂度。
比如 对于 2^270方 ,loglog 2^270 < 9!!!!
MASK数的妙用为我们对M位二进制的认识提供了新的角度,MASK数使得M位二进制可以以不同的方式存储、计算,值得思考与记忆。
本文虽非全部原创,但图片与对MASK数应用的思考确实是自己的果实。可以引用,但禁止转载、抄袭上述原创内容。
2018-08-01 00:45



