结对名单:031402224 彭巍 031402233 郑扬涛
一、问题描述
编码实现一个毕设导师的智能匹配的程序
输入:
- 30个老师(包含带学生数的要求的上限,单个数值,在[0,8]内)
- 100个学生(包含绩点信息),每个学生有5个导师志愿(志愿的导师可以重复但不能空缺)
输出:
- 导师和学生间的匹配信息(一个学生只能有一个确认导师,一个导师可以带少于等于其要求的学生数的学生)
- 未被分配到学生的导师
- 未被导师选中的学生
二、问题分析
学生角度:
根据学生对导师喜爱的程度,将五个志愿按照优先级排序,优先考虑志愿靠前的导师
对于每个学生有 \(student_{i}:choice_{1}>choice_{2}>choice_{3}>choice_{4}>choice_{5}\)
导师角度:
由于输入数据只有 绩点 这一评价标准,故每个导师在所有选他的学生中优先考虑绩点高的
(后期可以根据学生的专业知识修养、兴趣方向(学生想从事哪方面的研究)、创新能力等等综合信息来形成评价标准)
对于每个导师有 \(teacher_{i}:student_{1}>student_{2}>student_{3}>...>student_{n}\)
由于导师的分配会因为学生的偏好造成导师志愿的分布不均匀,这可能会导致有些学生分配不到导师,或者有的导师没有分配到学生,这就需要一些算法对此加以控制以达到最优匹配。
三、采用的算法
由于笔者有参加ACM竞赛,看到这个问题联想到图论中的 稳定婚姻问题(Stable marriage problem) 。查找了相关的文献资料后,发现导师分配问题是属于该问题的一个变形。而对于该问题,通常用 Gale-Shapley 算法来解决。
Gale-Shapley 算法简称 G-S 算法,也被称为延迟接受算法。该算法由 Gale 和 Shapley 提出,他们研究学校申请与婚姻稳定的匹配问题,并用 G-S算法得到了稳定的匹配, 这种匹配是帕累托最优。该算法只需在信息完全且充分的情况下,选择的双方按照自己的偏好进行排序,且一方先进行选择即可得出最优稳定匹配。
Gale-Shapley 算法的核心思想:
在信息对称且完全的情况下, 存在需要相互选择的集合 \(T = \left \{T_{1}, T_{2}, T_{3}, ..., T_{m} \right \}\) 与 \(S = \left \{S_{1}, S_{2}, S_{3}, ..., S_{n} \right \}\), 集合 \(S\) 中的个体 \(S_{i}\) 对 \(T\) 中的个体存在偏好如 \(S_{i} = \left \{T_{2}, T_{1}, T_{5}, ..., T_{m} \right \}\),表示对于 \(S_{i}\) 的第一选择为 \(T_{2}\),第二选择为 \(T_{1}\),第三选择为 \(T_{5}\),依次类推。 \(T\) 中个体 \(T_{r}\) 对 \(S\) 中的个体存在偏好 \(T_{r} = \left \{S_{6}, S_{3}, ..., S_{n} \right \}\)。 让 \(S\) 对 \(T\) 做出选择,即发出信息(如申请学校或求婚)。 当 \(T\) 接收信息的容量低于自己的需求量 \(K\) 时,全部暂时接受。 当 \(T\) 的接收信息容量超过自己需求量 \(K\) 时,\(T\) 根据自己的偏好从中进行选择,暂时接受其中处于偏好前面的 \(K\) 个,拒绝其他。被拒绝个体根据自己的第二偏好进行选择,并发出信息。若第二偏好的 \(T_{r}\) 未饱和,则暂时接受。若第二偏好的 \(T_{r}\) 饱和, 则 \(T_{r}\) 对包括上次选择的所有给自己发出信息的人按照偏好再次进行选择,并确定暂时接受的人和拒接的人。 被拒绝的人按照偏好顺序再次选择下一个偏好,依次类推……直到没有人剩下,整个匹配结束。 作为发出信息选择的一方占相对优势,被选择的一方占相对劣势。 但是随着选择次数的增多,稳定匹配时发出信息的一方会越处于偏好后方,而被选择的一方会越处于偏好前方。
四、算法步骤
根据原始的 Gale-Shapley 算法, 我们稍加修改后即可适用于原问题。
分配步骤:
按照学生在数据中的顺序根据当前志愿分配导师,若导师的学生数未满则直接把此学生分配给该导师;否则将此学生和已分配给该导师的学生中绩点最低的那个学生比较,若是此学生的绩点低于绩点最低的那个学生,则进入下一轮分配(下一轮分配考虑此生的下一个志愿);否则如果此学生的绩点高于绩点最低的那个学生,则将此生分配给该导师,绩点最低的那个学生则不再属于该导师,并将该学生的状态改为未分配。一直循环上述步骤,直到考虑了所有学生的所有志愿。
流程图:
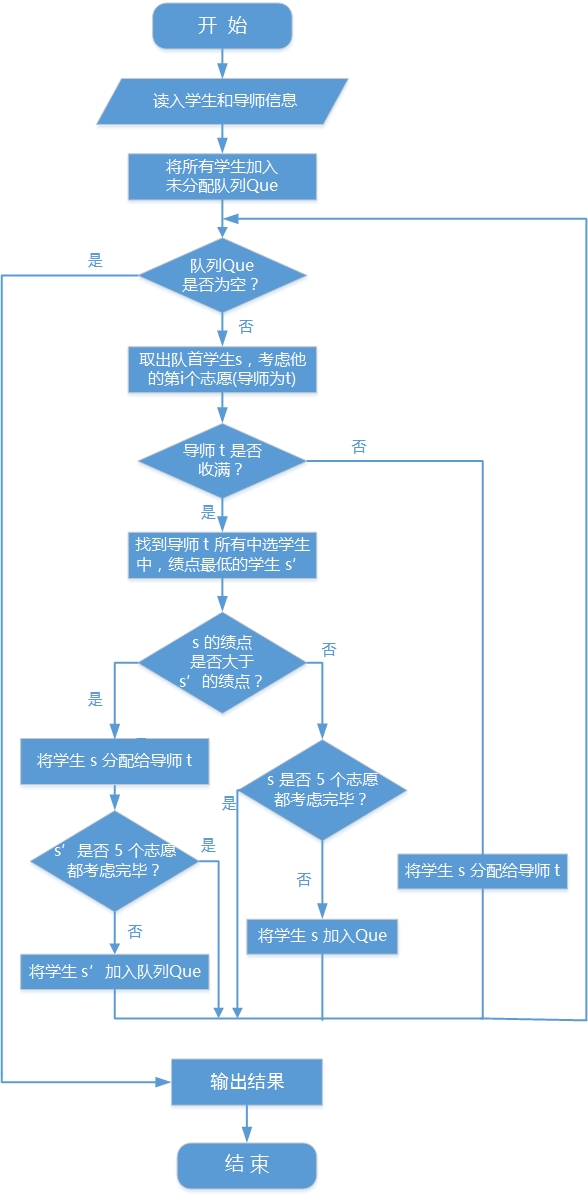
伪代码:
function Matching {
Initialize all s ∈ Student and t ∈ Teacher to free
while ∃ a free Student s who still has a choice t to choose {
t = first teacher on s's list to whom s has not yet chose
if t is free
distribute(s, t)
else some pair (s', t) already exists
if t prefers s to s'
distribute(s, t)
set s' to free
else
remain(s', t)
else
set s to free
}
}
五、代码实现
实现语言:C++
学生类
struct Student {
int student_id; // 学生编号
int teacher_id; // 中选的导师编号
int cur; // 当前分配进程正在考虑第cur个志愿
int want[5]; // 五个志愿
float point; // 绩点
};
导师类
struct Teacher {
int teacher_id; // 导师编号
int want_num; // 期望的学生数
int chose_num; // 已中选的学生数
int student_id[10]; // 中选的学生编号
};
分配系统
class DistributeSystem {
private:
int student_number; // 学生总人数
int teacher_number; // 导师总人数
Student* stu;
Teacher* tch;
public:
// 构造函数与析构函数
DistributeSystem() {}
DistributeSystem(int stu_num, int tch_num) {}
~DistributeSystem() {}
// 随机生成导师信息
void generate_teacher_information() {}
// 随机生成学生信息
void generate_student_information() {}
// 根据导师编号返回他在数组中的下标
int get_teacher_index(int teacher_id) {}
// 根据学生编号返回他在数组中的下标
int get_student_index(int student_id) {}
// 使用Gale–Shapley算法进行分配
void distribute() {
queue<Student> Que; //未分配到导师的学生队列
for (int i = 0; i < student_number; ++i) {
Que.push(stu[i]); // 初始都是未分配状态,都加进队列
}
while (!Que.empty()) {
Student& s = stu[get_student_index(Que.front().student_id)];
Que.pop();
// 考虑学生s的第cur个志愿(导师为t)
Teacher& t = tch[get_teacher_index(s.want[s.cur++])];
if (t.want_num > t.chose_num) { // 如果导师t还有剩余名额,直接中选
t.student_id[t.chose_num++] = s.student_id;
s.teacher_id = t.teacher_id;
} else {
int min_stu_id = -1; // 导师t中绩点最低的学生编号
int pos = -1; // 以及他在导师的中选列表中的下标
float min_point = 5.0;
for (int i = 0; i < t.chose_num; ++i) { // 在导师t中查找绩点最低的学生编号
Student tmp = stu[get_student_index(t.student_id[i])];
if (min_point > tmp.point) {
min_point = tmp.point;
min_stu_id = tmp.student_id;
pos = i;
}
}
// 如果导师t不带学生 或者 学生s的绩点比导师t所有已经中选学生的最低绩点还低,那么学生t只好再等下轮
if (t.want_num == 0 || s.point < min_point) {
if (s.cur < 5) { // 如果五个志愿还没考虑完毕的话,放入队列中继续参与分配
Que.push(s);
}
} else { // 不然学生t就直接替换掉绩点最低的那个学生
Student& min_stu = stu[get_student_index(min_stu_id)];
min_stu.teacher_id = -1;
if (min_stu.cur < 5) { // 被替换掉的学生再放入未分配的队列中去
Que.push(min_stu);
}
t.student_id[pos] = s.student_id;
s.teacher_id = t.teacher_id;
}
}
}
}
// 从导师角度查看分配结果
void get_teacher_result(bool flag) {}
// 从学生角度查看分配结果
void get_student_result(bool flag) {}
};
六、代码分析
对于我们的代码,分配的结果概括起来大概是这样:
- 分配导师的时候志愿的顺序很重要,只要绩点不是太低,且自己喜欢志愿顺序靠前,就会分配到自己喜欢的导师
- 分配的轮数越多,越是对导师有利(如果选这个导师的人比较多留下的都是绩点比较高的)
七、结果评估
为了评估该算法的实际效果,笔者随机生成了 10000 个样本对其进行测试。
样本约定:
- 导师的人数在
30 ~ 100人之间 - 学生的人数为导师的
1 ~ 4倍
将 10000 个样本分为 10 组,每组 1000 个,得到的结果如下表所示:
学生未分配率:
| 样本组数 | 最好情况 | 最坏情况 | 平均情况 |
|---|---|---|---|
| 1 | 0.0000% | 22.4806% | 1.5869% |
| 2 | 0.0000% | 16.9675% | 1.5230% |
| 3 | 0.0000% | 20.1681% | 1.6781% |
| 4 | 0.0000% | 18.6992% | 1.7076% |
| 5 | 0.0000% | 18.2609% | 1.5168% |
| 6 | 0.0000% | 28.0000% | 1.6612% |
| 7 | 0.0000% | 18.7500% | 1.5338% |
| 8 | 0.0000% | 18.0180% | 1.6950% |
| 9 | 0.0000% | 21.1180% | 1.6605% |
| 10 | 0.0000% | 22.5131% | 1.7302% |
| 平均 | 0.0000% | 20.4975% | 1.6293% |
学生中选志愿顺序:
| 样本组数 | 最好情况 | 最坏情况 | 平均情况 |
|---|---|---|---|
| 1 | 1.03030 | 2.00000 | 1.43622 |
| 2 | 1.05714 | 2.08264 | 1.42591 |
| 3 | 1.01818 | 2.01935 | 1.43242 |
| 4 | 1.02941 | 2.07207 | 1.43448 |
| 5 | 1.02857 | 1.97177 | 1.42840 |
| 6 | 1.04110 | 2.14433 | 1.43085 |
| 7 | 1.00000 | 2.04717 | 1.42317 |
| 8 | 1.06796 | 2.04819 | 1.43239 |
| 9 | 1.02041 | 2.15789 | 1.43456 |
| 10 | 1.02273 | 2.03759 | 1.43417 |
| 平均 | 1.03158 | 2.05810 | 1.43126 |
分析:
从上面可以看出,该算法的总体效果非常好。
对于学生未分配率来说,在最好情况下,所有学生都能得到分配。而在最坏情况竟然达到20%左右,这个数据一开始令笔者较为吃惊!后来在调试的过程中,将最坏情况下的输入数据进行输出查看,发现基本上都是出现在 学生的数量为导师的3倍多到4倍左右 以及 导师所期望带的学生数较少 这种极限数据情况下。对于通常情况,基本上学生的未分配率保持在1.6%左右。另一方面,对于学生中选的志愿,最好情况能够保证在第一志愿即可录取,而最差情况下也能够第二志愿录取。当然,没中选的学生是没有统计到该数据当中的(因为落选了,中选志愿更无从谈起)。
八、小结与感受
vvxyz: 总的来说这次作业抱了大腿,搭档是ACM的大神,这次编程的思路基本是按照搭档的思路走的,代码主要是搭档编写的,我们结对编程的时候,基本就是搭档是主力,我在旁边辅助,帮他纠正一些细节上的错误,改bug的时候帮助分析错误。这次结对编程的代码并没有很多难理解的地方,但是编程的过程中感受到了搭档强大清晰的逻辑思维以及扎实的c++基本功,这是值得我学习与思考的地方。
orzyt: 其实本次作业一开始搭档是想用 Java 配合数据库来写的,但由于我平常都是用C++来写算法,因此搭档为了配合我,后来就订下用C++编写。这里对搭档说一声感谢!对于此次结对编程题目,很切合实际,因为上学期我们刚刚经历过学生选导师这一环节。然后我是把这次作业当做一道ACM算法题目来写的(栋哥不要打我...),但是嘛,这次不只是为了AC这么简单。为了代码的规范性,以及更容易维护,我将算法的主要功能都封装在DistributeSystem类中。然后不得不说的就是debug的过程!在结对编程的第一天,我将代码的整体框架编写完毕,本地测试了学生数=100,导师数=30,以及其他几组数据,查看结果基本上符合预期,就将代码推送到git上去了。第二天,为了更好地评估该算法的实际效果,于是我就随机生成了一万个测试样本(详情见第七节),然后基本上程序跑着跑着就奔溃了。于是开始了漫长的debug过程,花费了一个晚上,进行各种花式调试,最终发现是 程序不能正确处理 导师期望数为0 的这种情况!!吐血...总之,在此次结对编程中,从建模、查文献、实现算法、样本测试一步步走过来,收获还是挺大的!
九、结对过程的闪光点
- 能够对原问题进行抽象建模
- 搭档之间相互支持鼓励,能够进行有效的沟通交流
- 懂得查找相关参考文献、学术论文等资料
十、代码仓库
点击查看:Distribute System
十一、参考文献
- Wikipedia. 稳定婚姻问题(Stable marriage problem)
- D. Gale and L. S. Shapley. College Admissions and the Stability of Marriage
- 向 冰,刘文君. 硕士研究生与导师的双向选择的最优匹配.
- 刘汝佳, 陈锋. 算法竞赛入门经典--训练指南



