正则化推导转载

正则化

通常来说，给机器学习的Loss函数中添加正则化可以防止过拟合。而在实际上的数学推导中，正则化的作用是使模型在达到最优解的时候，某些特征的参数\(w\)的取值更小甚至为0，从而降低模型的复杂度。而为什么减少参数\(w\)的取值能够防止过拟合，这点可能是直观的假定。

直观解释

这里拿Thaurun博客的图在直观上解释正则化的作用。

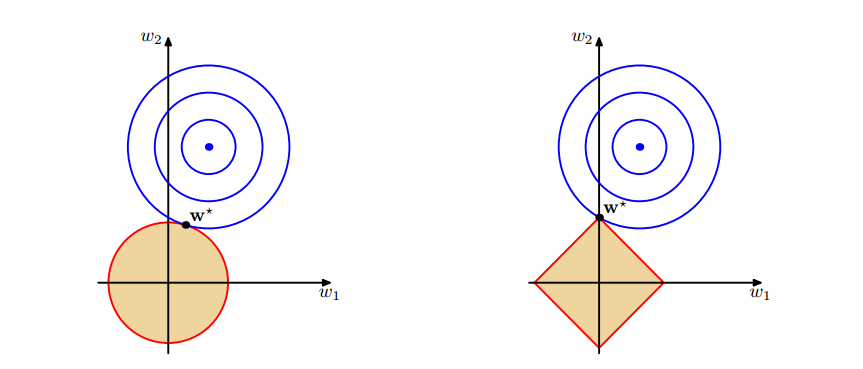
• 两图上面中的蓝色轮廓线是没有正则化损失函数的等高线，中心的蓝色点为最优解，左图的圆形、右图的矩形分别为L2、L1正则化给出的限制。
• 可以看到在正则化的限制之下，L2正则化给出的最优解w∗是使解更加靠近原点，也就是说L2正则化能降低参数范数的总和。
• L1正则化给出的最优解w∗是使解更加靠近某些轴，而其它的轴则为0，所以L1正则化能使得到的参数稀疏化。
  

L1正则化及其推导证明了L1正则化能够减少参数\(w\)的取值，并给出了直观的解释。
深入理解L1、L2正则化这篇从拉格朗日函数和概率分布的角度描述了正则化的意义