Silverlight动画基础八：动画与三角函数-绘制正弦/余弦曲线

正弦/余弦曲线,意思就是基于正弦、余弦的曲线函数。其函数周期为2π，其中x轴表示为角度（0-360度/2π），Y轴表示为当前角度产生的正弦/余弦值。

由此对应的坐标集合便形成了正弦/余弦曲线。

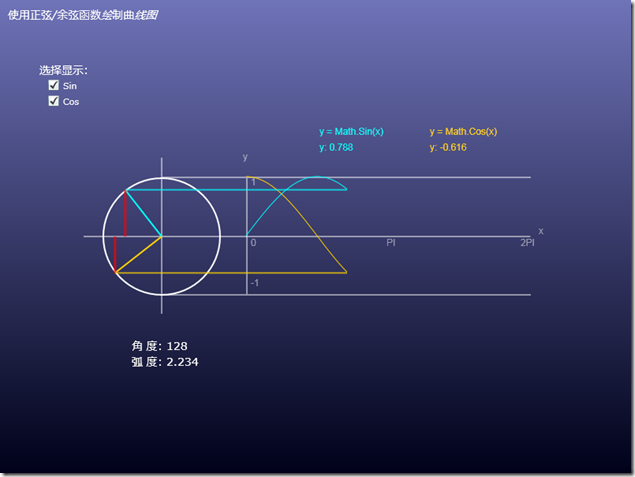
我们使用一个示例来演示如何使用Silverlight代码来画正弦/余弦曲线。这个示例分别画出了正弦、余弦曲线，并提供了两个选择框，可以选择显示那一个。

其原理是记录当前角度的正弦、余弦值(Y轴)和角度(X轴)形成坐标点，添加到坐标集合中，呈现出一种动态绘制的效果。

效果图如下：

 

由图中我们就能看到，现实了角度、角度的正弦、余弦值，当前坐标点。

 

根据之前的文章我们可以明确到，计算出指定角度/弧度的正弦或余弦值并不难。但在这个示例中需要控制的地方有4个：1.正弦、余弦两个情况下的直角边位置与高度、

2.半径位置、3.表示运动轨迹的直接的长度与位置、4.表示当前角度正弦、余弦的坐标点。

下面我们就直接看代码。这个示例中只使用一个XAML页面，unitCircleSin.xaml

 

unitCircleSin

unitCircleSin.xaml.cs代码如下，关键步骤看代码注释：

    public partial class unitCircleSin : Page
    {
        double SinAngle = 0;
        double CosAngle = 270;
        //每次递增角度
        double RotateSpeed = 1;
        //用于表示正弦半径
        Line SineRadius = new Line();
        //用于表示余弦半径 
        Line CosRadius = new Line();
        //单位圆心坐标点
        Point UnitCircleCenter = new Point();
        //正弦曲线坐标点集合
        PointCollection SinPoints = new PointCollection();
        //余弦曲线坐标点结合
        PointCollection CosPoints = new PointCollection();

        Point NextSinePoint = new Point();
        Point NextCosPoint = new Point();
        //用于表示正弦运动轨迹
        Line SinTracer = new Line();
        //用于表示余弦运动轨迹
        Line CosTracer = new Line();

        //正弦直角边
        Line SinRightAngles = new Line();
        //余弦直角边
        Line CosRightAngles = new Line();

        //显示、隐藏正弦、余弦曲线
        bool SineHidden = false;
        bool CosineHidden = false;
       

        public unitCircleSin()
        {
            InitializeComponent();
            //获取圆心坐标
            UnitCircleCenter.X = (double)UnitCircle.GetValue(Canvas.LeftProperty) + UnitCircle.Width / 2;
            UnitCircleCenter.Y = (double)UnitCircle.GetValue(Canvas.TopProperty) + UnitCircle.Height / 2;

            //初始正弦半径
            SineRadius.StrokeThickness = 2;
            SolidColorBrush SineStroke = new SolidColorBrush();
            SineStroke.Color = Color.FromArgb(255, 0, 255, 255);
            SineRadius.Stroke = SineStroke;
            Radii.Children.Add(SineRadius);

            //初始余弦半径
            CosRadius.StrokeThickness = 2;
            SolidColorBrush CosStroke = new SolidColorBrush();
            CosStroke.Color = Color.FromArgb(255, 255, 210, 0);
      
            CosRadius.Stroke = CosStroke;
            Radii.Children.Add(CosRadius);
            //初始位置
            SineRadius.X1 = SineRadius.X2 = CosRadius.X1 = CosRadius.X2 = (double)UnitCircleCenter.X;
            SineRadius.Y1 = SineRadius.Y2 = CosRadius.Y1 = CosRadius.Y2 = (double)UnitCircleCenter.Y;

            //初始正弦轨迹
            SinTracer.StrokeThickness = 2;
            SolidColorBrush SinTracerStroke = new SolidColorBrush();
            SinTracerStroke.Color = Color.FromArgb(180, 0, 255, 255);
            SinTracer.Stroke = SinTracerStroke;
            LayoutRoot.Children.Add(SinTracer);
            //初始余弦轨迹
            CosTracer.StrokeThickness = 2;
            SolidColorBrush CosTracerStroke = new SolidColorBrush();
            CosTracerStroke.Color = Color.FromArgb(180, 255, 210, 0);
            CosTracer.Stroke = CosTracerStroke;
            LayoutRoot.Children.Add(CosTracer);

            //初始正弦直角边
            SinRightAngles.StrokeThickness = 3;
            SolidColorBrush SinRightAngleStroke = new SolidColorBrush();
            SinRightAngleStroke.Color = Color.FromArgb(180, 255, 0, 0);
            SinRightAngles.Stroke = SinRightAngleStroke;
            LayoutRoot.Children.Add(SinRightAngles);
            //初始余弦直角边
            CosRightAngles.StrokeThickness = 3;
            SolidColorBrush CosRightAngleStroke = new SolidColorBrush();
            CosRightAngleStroke.Color = Color.FromArgb(180, 255, 0, 0);
            CosRightAngles.Stroke = CosRightAngleStroke;
            LayoutRoot.Children.Add(CosRightAngles);

            //设置两个曲线的初始位置
            Sinewave.SetValue(Canvas.LeftProperty, 312.00);
            Sinewave.SetValue(Canvas.TopProperty, -1.00);
            Cosinewave.SetValue(Canvas.LeftProperty, 312.00);
            Cosinewave.SetValue(Canvas.TopProperty, -1.00);

            DrawTimer.Completed += new EventHandler(drawSine);
            ClearTimer.Completed += new EventHandler(clearTimer_Completed);
            ChkSin.Unchecked += new RoutedEventHandler(chkSin_Unchecked);
            ChkSin.Checked += new RoutedEventHandler(chkSin_Checked);
            ChkCos.Unchecked += new RoutedEventHandler(chkCos_Unchecked);
            ChkCos.Checked += new RoutedEventHandler(chkCos_Checked);
           
            DrawTimer.Begin();
        }

        #region 控制 显示/隐藏曲线
        void chkCos_Checked(object sender, RoutedEventArgs e)
        {
            //控制显示余弦曲线
            Cosinewave.Visibility = Visibility.Visible;
            MsgCosY.Visibility = Visibility.Visible;
            MsgYcos.Visibility = Visibility.Visible;
            CosRightAngles.Visibility = Visibility.Visible;
            CosTracer.Visibility = Visibility.Visible;
            CosRadius.Visibility = Visibility.Visible;
            CosineHidden = false;
        }

        void chkCos_Unchecked(object sender, RoutedEventArgs e)
        {
            //控制隐藏余弦曲线
            Cosinewave.Visibility = Visibility.Collapsed;
            MsgCosY.Visibility = Visibility.Collapsed;
            MsgYcos.Visibility = Visibility.Collapsed;
            CosRightAngles.Visibility = Visibility.Collapsed;
            CosTracer.Visibility = Visibility.Collapsed;
            CosRadius.Visibility = Visibility.Collapsed;
            CosineHidden = true;
        }

        void chkSin_Checked(object sender, RoutedEventArgs e)
        {
            //控制显示正弦曲线
            Sinewave.Visibility = Visibility.Visible;
            MsgSinY.Visibility = Visibility.Visible;
            MsgYsin.Visibility = Visibility.Visible;
            SinRightAngles.Visibility = Visibility.Visible;
            SinTracer.Visibility = Visibility.Visible;
            SineRadius.Visibility = Visibility.Visible;
            SineHidden = false;
        }

        void chkSin_Unchecked(object sender, RoutedEventArgs e)
        {
            //控制隐藏正弦曲线
            Sinewave.Visibility = Visibility.Collapsed;
            MsgSinY.Visibility = Visibility.Collapsed;
            MsgYsin.Visibility = Visibility.Collapsed;
            SinRightAngles.Visibility = Visibility.Collapsed;
            SinTracer.Visibility = Visibility.Collapsed;
            SineRadius.Visibility = Visibility.Collapsed;
            SineHidden = true;
        }
        #endregion
       
        void clearTimer_Completed(object sender, EventArgs e)
        {

            ClearTimer.Stop();
            SinPoints.Clear();
            CosPoints.Clear();
            DrawTimer.Begin();
            SinAngle = 0;
            CosAngle = 270;
            NextSinePoint.X = 0;
            NextCosPoint.X = 0;
            if (!SineHidden) SinRightAngles.Visibility = Visibility.Visible;
            if (!CosineHidden) CosRightAngles.Visibility = Visibility.Visible;
        }

        void drawSine(object sender, EventArgs e)
        {

            //当角度运行一周后重新，重新设置初始值，并开始
           if (SinAngle == -361)
            {
                SinAngle = 0;
                SineRadius.X2 = UnitCircleCenter.X + Math.Cos(DegreesToRadians(SinAngle)) * UnitCircle.Width / 2;
                SineRadius.Y2 = UnitCircleCenter.Y + Math.Sin(DegreesToRadians(SinAngle)) * UnitCircle.Height / 2;
                CosAngle = 270;
                CosRadius.X2 = UnitCircleCenter.X + Math.Cos(DegreesToRadians(CosAngle)) * UnitCircle.Width / 2;
                CosRadius.Y2 = UnitCircleCenter.Y + Math.Sin(DegreesToRadians(CosAngle)) * UnitCircle.Height / 2;
                SinRightAngles.Visibility = Visibility.Collapsed;
                CosRightAngles.Visibility = Visibility.Collapsed;
                ClearTimer.Begin();
            }
            else
            {
                //计算正弦、余弦半径的结束点位置
                SineRadius.X2 = UnitCircleCenter.X + Math.Cos(DegreesToRadians(SinAngle)) * UnitCircle.Width / 2;
                SineRadius.Y2 = UnitCircleCenter.Y + Math.Sin(DegreesToRadians(SinAngle)) * UnitCircle.Height / 2;
                CosRadius.X2 = UnitCircleCenter.X + Math.Cos(DegreesToRadians(CosAngle)) * UnitCircle.Width / 2;
                CosRadius.Y2 = UnitCircleCenter.Y + Math.Sin(DegreesToRadians(CosAngle)) * UnitCircle.Height / 2;

                //记录正弦曲线坐标点
                //由于X轴位于页面的中间，单位圆的直径是150
                //因此分别用这两个值来计算Y轴坐标点。X轴值每次加1，初始值为0.
                double sine = Math.Sin(DegreesToRadians(-SinAngle));
                NextSinePoint.Y = this.Height / 2 - (sine * 75);
                SinPoints.Add(NextSinePoint);
                Sinewave.Points = SinPoints;

                //记录余弦曲线坐标点
                double cosine = Math.Cos(DegreesToRadians(-SinAngle));
                NextCosPoint.Y = this.Height / 2 - (cosine * 75);
                CosPoints.Add(NextCosPoint);
                Cosinewave.Points = CosPoints;


                SinTracer.X1 = SinRightAngles.X1 = SinRightAngles.X2 = SineRadius.X2;
                SinTracer.Y1 = SinRightAngles.Y1 = SineRadius.Y2;
                SinTracer.X2 = NextSinePoint.X + 312;
                SinTracer.Y2 = NextSinePoint.Y;
                SinRightAngles.Y2 = UnitCircleCenter.Y;

                CosTracer.X1 = CosRightAngles.X1 = CosRightAngles.X2 = CosRadius.X2;
                CosTracer.Y1 = CosRightAngles.Y1 = CosRadius.Y2;
                CosTracer.X2 = NextCosPoint.X + 312;
                CosTracer.Y2 = NextCosPoint.Y;
                CosRightAngles.Y2 = UnitCircleCenter.Y;

                MsgDegrees.Text = "角 度: " + -SinAngle;
                MsgRadians.Text = "弧 度: " + String.Format("{0:0.000}", DegreesToRadians(-SinAngle));
                MsgYsin.Text = "y: " + String.Format("{0:0.000}", sine);
                MsgYcos.Text = "y: " + String.Format("{0:0.000}", cosine);

                NextSinePoint.X += 1;
                NextCosPoint.X += 1;
                SinAngle -= RotateSpeed;
                CosAngle -= RotateSpeed;
                DrawTimer.Begin();
            }
        }


        double RadiansToDegrees(double Radians)
        {
            return Radians * Math.PI / 180;
        }

        double DegreesToRadians(double Degrees)
        {
           return Degrees * Math.PI / 180;
        }
    }

整体上简单来讲，依然是正弦、余弦函数、弧度、角度的运用。

 

unitCircleSin.xaml 代码

<UserControl.Resources>
    <Storyboard x:Name="DrawTimer" Duration="00:00:00.00"/>
    <Storyboard x:Name="ClearTimer" Duration="00:00:03.00"/>
</UserControl.Resources>

<Canvas Height="600" x:Name="LayoutRoot" Width="800">
    <Canvas.Background>
        <LinearGradientBrush EndPoint="0.5,1" StartPoint="0.5,0">
            <GradientStop Color="#FF6F73B9"/>
            <GradientStop Color="#FF000119" Offset="1"/>
        </LinearGradientBrush>
    </Canvas.Background>
    <Canvas Height="377.25" Width="569" Canvas.Left="105" x:Name="SinePlotter">
        <Path Height="2.472" Width="568.5" Stretch="Fill" Stroke="#FFFFFFFF" StrokeThickness="2" 
              Data="M189,299 L-8.0025377,299" Opacity="0.5" Canvas.Top="299"/>
        <Path Height="2" Width="200" Stretch="Fill" Stroke="#FFFFFFFF" StrokeThickness="2" 
              Data="M189,299 L-8.0025377,299" RenderTransformOrigin="0.5,0.5" 
              Opacity="0.5" Canvas.Top="298">
            <Path.RenderTransform>
                <TransformGroup>
                    <ScaleTransform/>
                    <SkewTransform/>
                    <RotateTransform Angle="90"/>
                    <TranslateTransform/>
                </TransformGroup>
            </Path.RenderTransform>
        </Path>
        <Path Height="2" Width="469" Opacity="0.5" Stretch="Fill" Stroke="#FFFFFFFF" StrokeThickness="2" 
              Data="M189,299 L-8.0025377,299" Canvas.Left="100" Canvas.Top="224"/>
        <Path Height="2" Width="469" Opacity="0.5" Stretch="Fill" Stroke="#FFFFFFFF" StrokeThickness="2" 
              Data="M189,299 L-8.0025377,299" Canvas.Left="100" Canvas.Top="373"/>
        <Path Height="149" Width="2" Fill="#FFFFFFFF" Stretch="Fill" Stroke="#FFFFFFFF" StrokeThickness="2" 
              Data="M223,374.5 L223,225.43207" Opacity="0.5" Canvas.Left="207" Canvas.Top="224.932"/>
        <TextBlock Text="y" TextWrapping="Wrap" Canvas.Top="192" 
                   Canvas.Left="203" Foreground="#FFFFFFFF" Opacity="0.5"/>
        <TextBlock Foreground="#FFFFFFFF" Text="1" TextWrapping="Wrap" 
                   Canvas.Left="213" Canvas.Top="224" Opacity="0.5"/>
        <TextBlock Foreground="#FFFFFFFF" Text="0" TextWrapping="Wrap" 
                   Canvas.Left="213" Canvas.Top="301" Opacity="0.5"/>
        <TextBlock Foreground="#FFFFFFFF" Text="-1" TextWrapping="Wrap" 
                   Canvas.Left="213" Canvas.Top="352" Opacity="0.5"/>
        <TextBlock Foreground="#FFFFFFFF" Text="x" TextWrapping="Wrap" 
                   Canvas.Left="578" Canvas.Top="286" Opacity="0.5"/>
        <TextBlock Foreground="#FFFFFFFF" Text="PI" TextWrapping="Wrap" 
                   Canvas.Left="385" Canvas.Top="301" Opacity="0.5"/>
        <TextBlock Foreground="#FFFFFFFF" Text="2PI" TextWrapping="Wrap"
                   Canvas.Left="555" Canvas.Top="301" Opacity="0.5"/>
        <TextBlock x:Name="MsgSinY" Text="y = Math.Sin(x)" TextWrapping="Wrap" 
                   Canvas.Top="160" Canvas.Left="300" Foreground="#FF00FFFF" />
        <TextBlock Text="y = 0" TextWrapping="Wrap" Canvas.Top="180" Canvas.Left="300" 
                   Foreground="#FF00FFFF" x:Name="MsgYsin"/>
        <TextBlock Text="y = Math.Cos(x)" TextWrapping="Wrap" Foreground="#FFFFD200" 
                   x:Name="MsgCosY" Canvas.Top="160" Canvas.Left="440"/>
        <TextBlock Text="y = 0" TextWrapping="Wrap" Foreground="#FFFFD200" x:Name="MsgYcos"
                   Canvas.Top="180" Canvas.Left="440"/>
    </Canvas>
    <Canvas Height="600" Width="800" x:Name="Radii">

    </Canvas>
    <TextBlock Height="29" Width="388" Canvas.Top="9.975" Text="使用正弦/余弦函数绘制曲线图" TextWrapping="Wrap" 
               Foreground="#FFFFFFFF" x:Name="MsgBlock" FontFamily="Verdana" 
               FontSize="14" FontStyle="Italic" Canvas.Left="10"/>
    <TextBlock FontFamily="Verdana" FontSize="14" Foreground="#FFFFFFFF" Text="角  度: 0" TextWrapping="Wrap" 
               Canvas.Left="167" Canvas.Top="430" x:Name="MsgDegrees"/>
    <TextBlock FontFamily="Verdana" FontSize="14" Foreground="#FFFFFFFF" Text="弧  度: 0" TextWrapping="Wrap" 
               Canvas.Left="167" Canvas.Top="450" x:Name="MsgRadians"/>
    <Polyline x:Name="Sinewave" Points="" Stroke="#FF00FFFF" StrokeThickness="1" FillRule="EvenOdd"/>
    <Polyline x:Name="Cosinewave" Points="" Stroke="#FFFFD200" StrokeThickness="1" FillRule="EvenOdd"/>
    <Ellipse Height="150" Width="150" Stroke="#FFFFFFFF" StrokeThickness="2" x:Name="UnitCircle" 
             Canvas.Left="130" Canvas.Top="225"/>
    <TextBlock Text="选择显示:" TextWrapping="Wrap" Canvas.Top="80" Canvas.Left="50" 
               Foreground="#FFFFFFFF" FontFamily="Verdana" 
               FontSize="14" x:Name="MsgShow"/>
    <CheckBox Content="Sin" Canvas.Top="100" Canvas.Left="60" Foreground="#FFFFFFFF" x:Name="ChkSin" IsChecked="True"/>
    <CheckBox x:Name="ChkCos" Foreground="#FFFFFFFF" Content="Cos" Canvas.Left="60" Canvas.Top="120" IsChecked="True"/>
</Canvas>

 

在线演示地址：点击查看

总结：从整个示例角度来讲，无论是记录运动轨迹、绘制曲线，都是使用了三角函数公式进行运算的结果，

此示例的目的，首先是通过动态绘制演示了正弦、余弦函数、曲线等之间的关系，其次是通过代码演练了三角函数的使用。

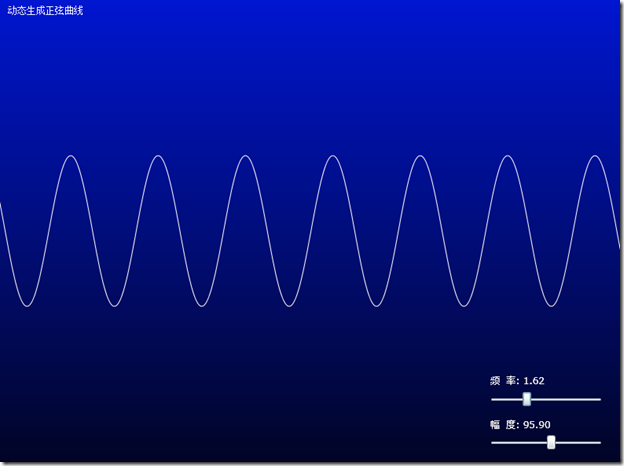
下面再看一个简单的例子，用于演示正弦曲线。

 

SineWaveGenerator

这个示例使用正弦函数动态绘制曲线。根据频率与振幅这两个参数的变更进行绘制曲线。这个示例比较容易些。

效果图如下：

 

具体代码如下：

SineWaveGenerator.xaml.cs 代码：

public partial class SineWaveGenerator : Page
   {
       //当前角度，用于计算角度的正弦
   private double Angle = 0;
       //曲线坐标点集合
   private PointCollection PC = new PointCollection();
       //每次计算出的坐标点
   private Point NextPoint = new Point();
       //振幅，理解为圆的半径大小。
   private double Amplitude = 145;
       //频率，角度每次变更的系数。
   private double Frequency = .5; 


       public SineWaveGenerator()
       {
           InitializeComponent();

           FrequencySlider.Minimum = 0;
           FrequencySlider.Maximum = 5;
           FrequencySlider.Value = Frequency;
           MsgFrequency.Text = "频  率: " + FrequencySlider.Value;

           AmplitudeSlider.Minimum = 0;
           AmplitudeSlider.Maximum = 175;
           AmplitudeSlider.Value = Amplitude;
           MsgAmplitude.Text = "幅  度: " + AmplitudeSlider.Value;

           FrequencySlider.ValueChanged += new RoutedPropertyChangedEventHandler<double>(slider_ValueChanged);
           AmplitudeSlider.ValueChanged += new RoutedPropertyChangedEventHandler<double>(slider_ValueChanged);

           DrawSine();
       }

       private void slider_ValueChanged(object sender, RoutedPropertyChangedEventArgs<double> e)
       {
           //清理曲线坐标点集合
             PC.Clear();
           Frequency = FrequencySlider.Value;
           Amplitude = AmplitudeSlider.Value;
           MsgAmplitude.Text = "幅  度: " + String.Format("{0:0.00}", AmplitudeSlider.Value);
           MsgFrequency.Text = "频  率: " + String.Format("{0:0.00}", FrequencySlider.Value);

           DrawSine();
       }

       private void DrawSine()
       {
           for (int i = 0; i < this.Width; i++)
           {
               //计算角度，角度大小受频率大小影响
                  Angle += (Math.PI / 180 * 2) * Frequency;
               
               //根据振幅计算、角度计算坐标点
                  NextPoint.X = i;
               NextPoint.Y = this.Height / 2 - (Math.Sin(Angle) * Amplitude);
               //添加坐标点。
                 PC.Add(NextPoint);
               Poly.Points = PC;
           }
       }

   }

 

SineWaveGenerator.xaml 代码：

<Canvas Width="800" Height="600" x:Name="LayoutRoot">
    <Canvas.Background>
        <LinearGradientBrush EndPoint="0.5,1" StartPoint="0.5,0">
            <GradientStop Color="#FF010424" Offset="1"/>
            <GradientStop Color="#FF0016D3" Offset="0"/>
        </LinearGradientBrush>
    </Canvas.Background>
    
    <Border Height="600" Width="800" BorderBrush="#FFFFFFFF" BorderThickness="1,1,1,1"/>
    
    <Polyline x:Name="Poly" Points="" Stroke="#FFFFFFFF" StrokeThickness="1" FillRule="EvenOdd"/>
    
    <TextBlock x:Name="MsgBlock" Width="197" Height="24" Text="动态生成正弦曲线" TextWrapping="Wrap" 
               Canvas.Top="12" Canvas.Left="14" Foreground="#FFFFFFFF" HorizontalAlignment="Stretch"/>
    
    <Slider  x:Name="FrequencySlider" Canvas.Top="505" Width="150" 
             Canvas.Left="624" SmallChange="0.25"/>
    <TextBlock x:Name="MsgFrequency" Text="频  率: 0" TextWrapping="Wrap" Canvas.Top="483" Canvas.Left="628" 
               Foreground="#FFFFFFFF" FontFamily="Verdana" FontSize="12" />
    
    <Slider  x:Name="AmplitudeSlider" Width="150" Canvas.Top="560" 
             Canvas.Left="624" Maximum="100" SmallChange="1"/>
    <TextBlock  x:Name="MsgAmplitude" Text="幅  度: 0" TextWrapping="Wrap" Canvas.Top="539" Canvas.Left="628" 
               Foreground="#FFFFFFFF" FontFamily="Verdana" FontSize="12"/>
</Canvas>

在线演示地址：点击查看

总结：这个示例的目的是通过一个简单的效果换个角度去看待使用正弦函数，当然这个绘制过程也可以使用动画进行控制，

或者在故事版与正弦与余弦函数结合，比如可以让一个物体根据已经生成好的坐标集合进行运动。可以做出很多很好玩的效果。

 

 

【注：本文技术论点源于《Foundation Silverlight 3 Animation》,个人理解可能存在差异,请参考原著】