用传统流程图表示求解以下问题的算法。 1. 有两个瓶子A和B,分别盛放醋和酱油,要求将他们互换依次将10个数输入,要求输出其中最大的数
用传统流程图表示求解以下问题的算法。
-
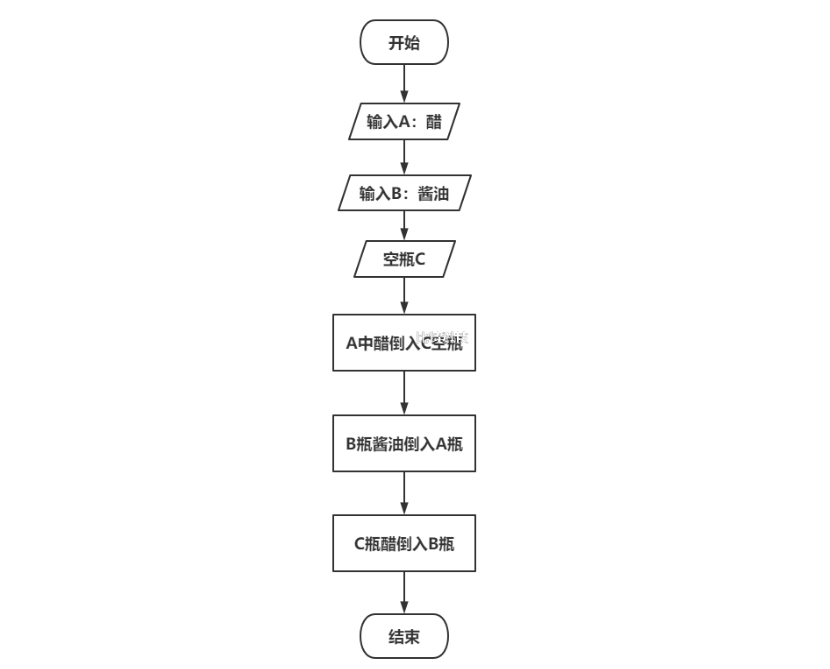
有两个瓶子A和B,分别盛放醋和酱油,要求将他们互换(即A瓶原来盛醋,现在盛酱油,B瓶则相反)。
解析:
用两个瓶子显然很难实现,可以借助一个空瓶子C作为中转,先将A中醋导入C中,然后将B中的酱油导入A中,最后将C中的醋导入B中即可实现交换。
-
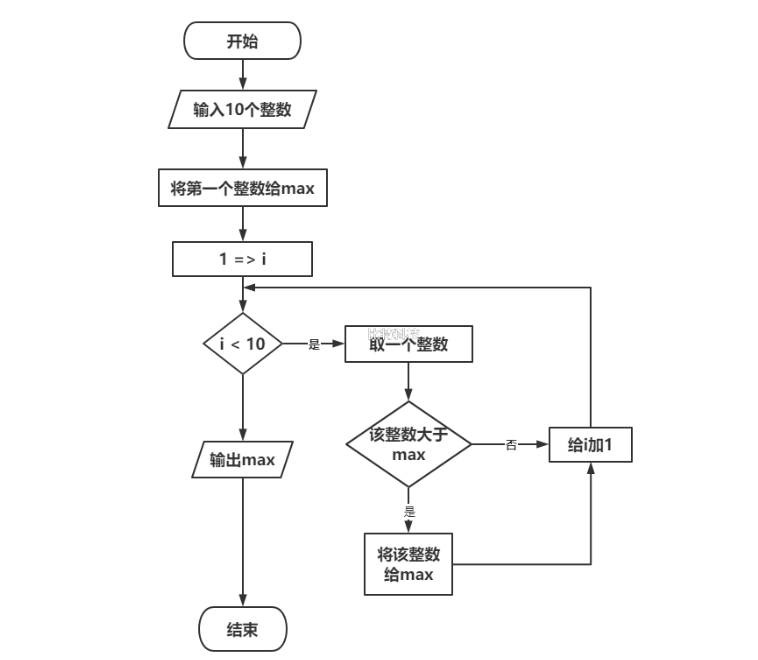
依次将10个数输入,要求输出其中最大的数。
解析:
先输入10个整数,将第一个整数给max,然后依次取剩余整数与max进行比较,如果某个整数大于max,将该整数交给max,直到所有剩余整数全部比较完,max中保存的即为最大整数,将max值输出。
-
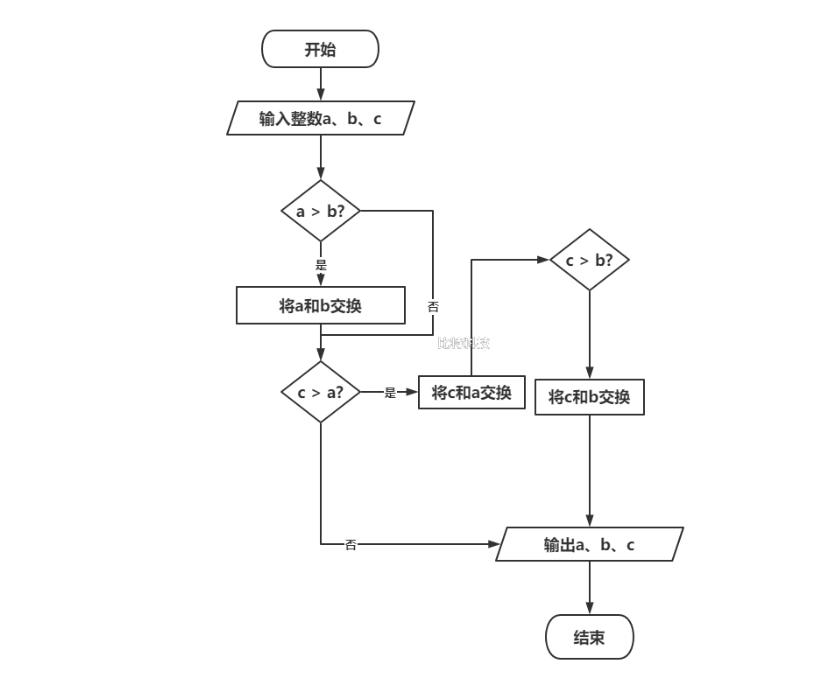
有3个数a,b,c, 要求按大小顺序把他们输出。
解析:
i:先用a和b比较,如果a大于b,将a与b内容交换,否则进行ii
ii:用c和a比较,如果c大于a,将a和c交换,否则进行iv
iii:用c和b比较,如果c大于b,将c和b进行交换,否则进行iv
iv:输出a、b、c,结束
-
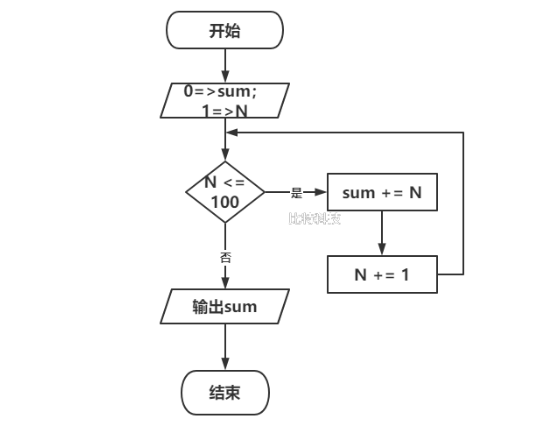
求1 + 2 + 3 + ... + 100。
解析:
给定N为1,sum为0,如果N 小于等于100时,进行sum += N,直到N超过100,循环操作完成后sum即为从1加到100的结果。
![求1 + 2 + 3 + ... + 100]()
-
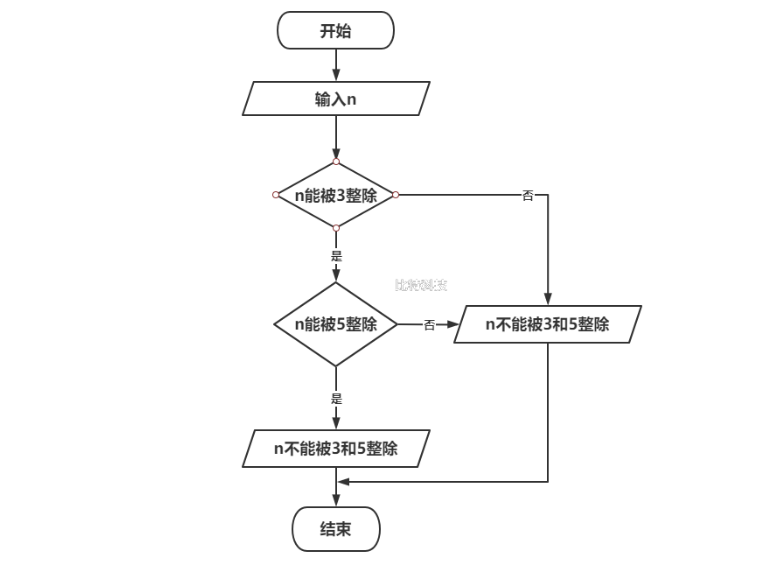
判断一个数n能否同时被3和5整除。
解析:
i:输入数据n
ii:如果n能被3整数,进行iii,否则输出n不能被3和5整数
iii:如果n能被5整数,输出n能被3和5整数,否则n不能被3和5整数
-
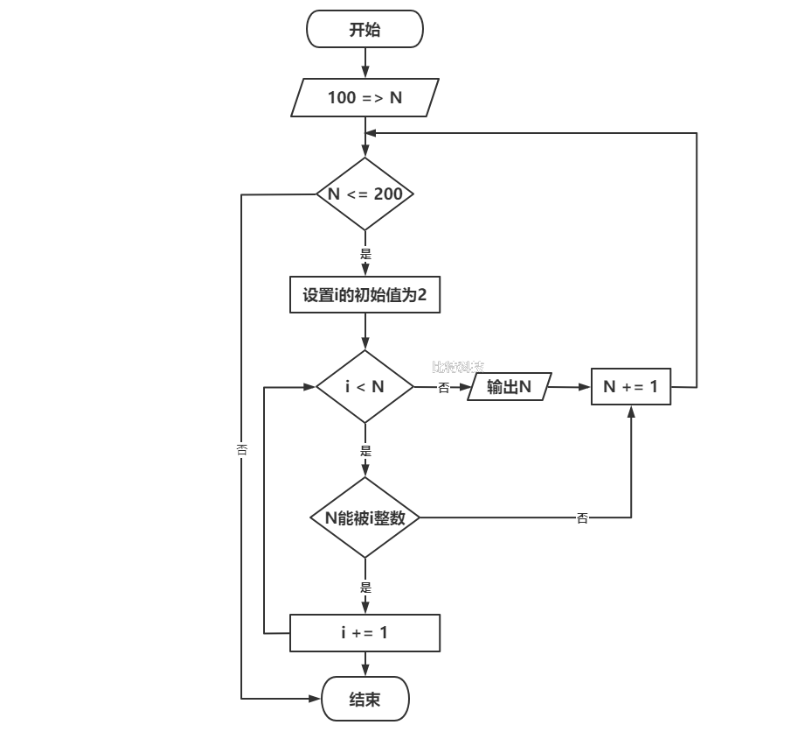
将100~200之间的素数输出
素数:即数学中的质数,因子只有1和其本身的数字称为质数。
对100和200之间的每个数进行一下操作:
该数能否被2~该数之间的所有数整除,是则是素数输出,否则取下一个数字。
-
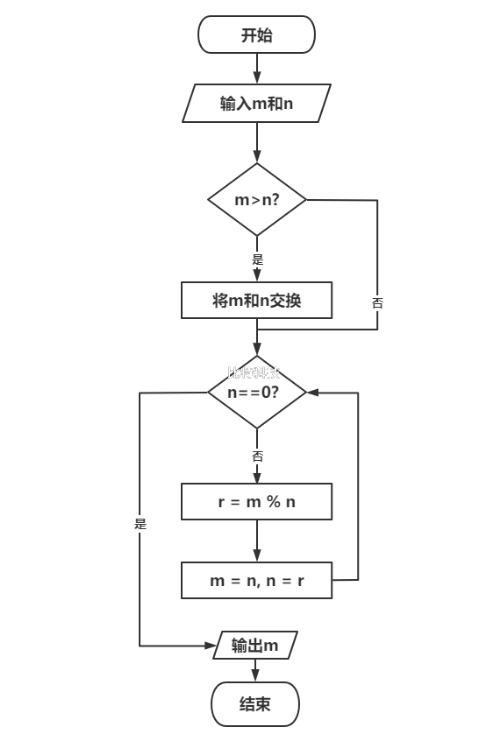
求两个数m和n的最大公约数
解析:辗转相除法
a. 如果m大于n,交换m和n
b. 循环进行一下操作:
n是否为0? 是则最大公约数为m,输出m结束。
否则:用m%n结果给r,将n的值给m,将r的值给n
-
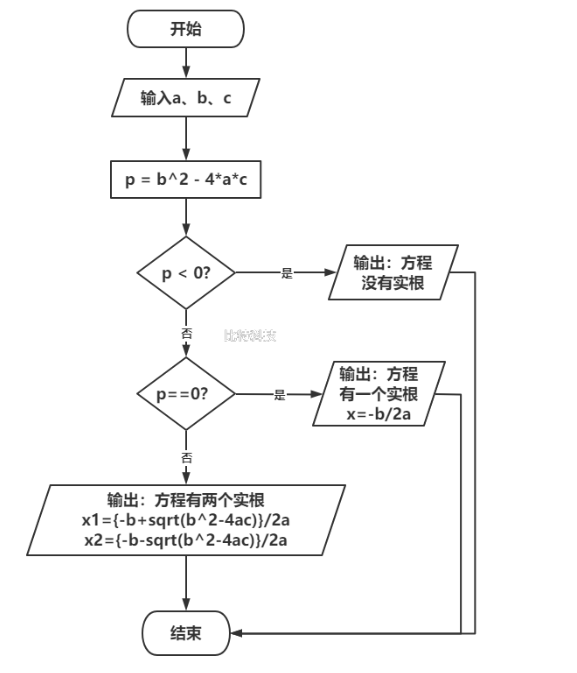
求方程\(ax^2 + bx + c = 0\)的根。分别考虑:
- 有两个不相等的实根;
- 有两个相等的实根;
解析:
如果\(b^2 - 4ac > 0\)则方程有两个不相等的实根:\(x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}\)
如果\(b^2 - 4ac = 0\)则方程有一个实根:\(x=\frac{-b}{2a}\)
如果\(b^2 - 4ac < 0\)则方程没有实根。
关注公众号 牛顿顿的星空 在里面回复 谭浩强答案,获取完整版答案,有问题也可以公众号后台私信我


 浙公网安备 33010602011771号
浙公网安备 33010602011771号