蒙特卡洛树搜索（MonteCarlo Tree Search）MCTS
AlphaGo， AlphaZero 的成功，让原本小众的MCTS火了一把。
MCTS算法的产生是以决策论、博弈论、蒙特卡洛方法以及老.虎.机算法为基础的。
在决策论中，主要涉及马尔可夫决策过程Markov Decision Processes (MDPs): MDPs是对智能体(agent)在环境(environment)中连续决策进行建模，agent当前的动作不仅对当前产生影响，而且还会对将来的的情况产生影响，如果从奖励的角度，即MDPs不仅影响即时的奖励，而且还会影响将来的长期奖励，因此，MDPs需要对即时奖励与长期奖励的获得进行权衡。
博弈论，将决策论扩展到多智能体交互过程。多个智能体的决策过程中， 如果没有智能体可以通过单方面的转换策略而受益，则多个智能体的策略组合形成了纳什均衡。
MCTS迭代地构建搜索树，直到达到预先设定的停止条件，比如迭代步数，迭代时间，迭代耗费的内存等等。
搜索树中每个节点代表着一种状态，而每条边代表着动作。MCTS包括每次迭代大体不包含四个过程。即选择、扩展、模拟和反向传播。
选择： 从根据节点开始，然后递归地向下执行子节点选择策略，直到达到最达到一个不完全扩展节点（即此节点的仍有未访问的子节点）;
扩展：从不完全扩展节点中选择一个未访问的子节点；
模拟: 从未经访问的节点开始执行默认策略向下递归，直到到达叶子节点，产生结果；
回溯：根据模拟产生的结果，反向更新路径上每个节点的信息。
在选择与扩展过程中，涉及选择策略，在模拟过程中也涉及向下递归的策略。
# 一般MCTS算法：
def mcts(v0):
"""
v: 节点， 代表状态， v0 起始状态，vl是从v0开始一直向下递归迭代选择后到达不完全扩展节点后，选择的某一个未访问后子节点。
action:
"""
while ! stop_conditions:
vl = expand_policy(v0)
reward = simulation_policy(vl)
backup(vl,reward)
return action(select_policy(v0))
def expand_policy(v):
while v is not terminal_leaf:
if v not full expanded:
return unvisited_child(v)
else:
return select_policy(v)
def select_policy(v):
return max([uct(child) for child in v.children])
def uct(v):
return v.total_reward/v.visit_num + c * sqrt(2 ln(v.parent.visit_num)/v.visit_num)
def similuation_policy(v):
while v if not terminal:
v = random_select_child(v)
return reward(v)
def backup(v, reward):
while v is not None:
v.visit_num +=1
v.total_reward +=reward
v = v.parent
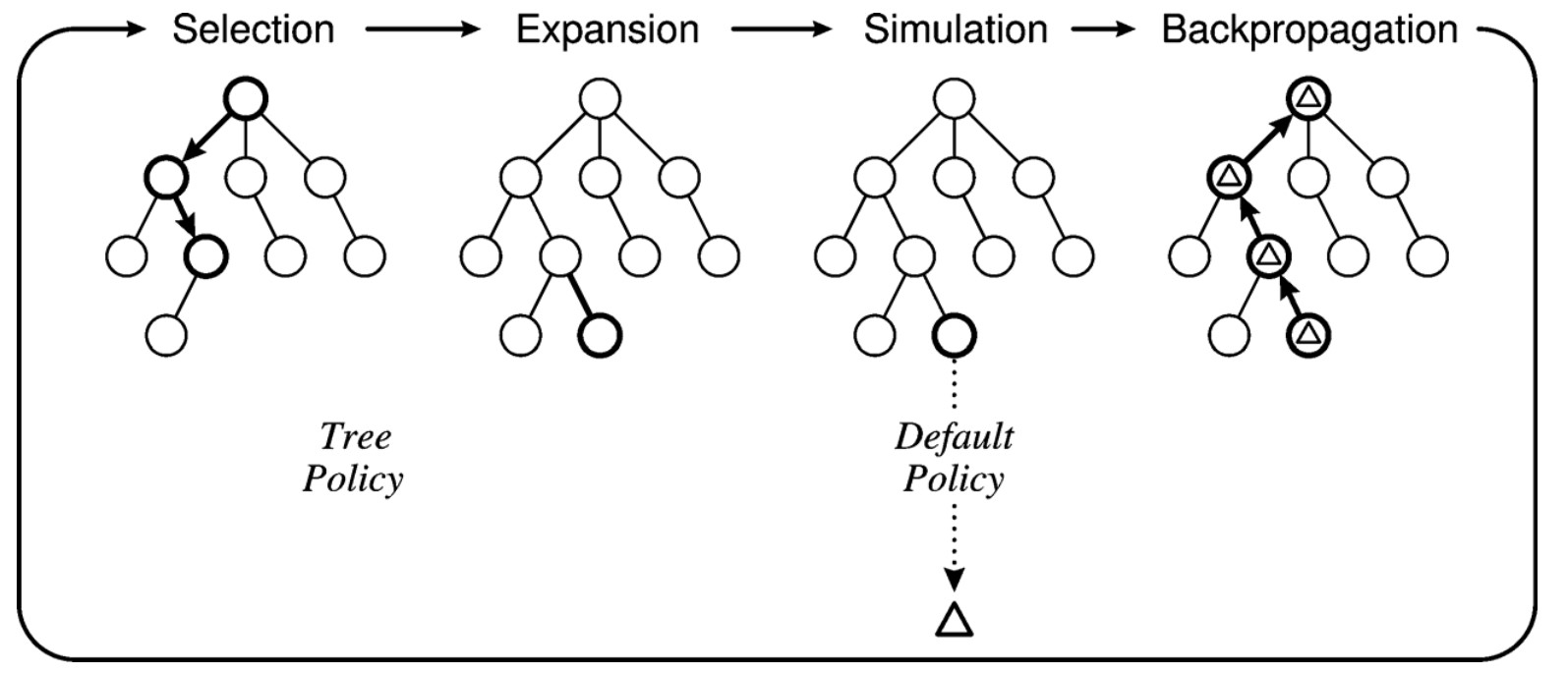
下图即展示了MCTS的一次迭代，在选择部分,从根节点一直向下迭代，直到到达某一不完全扩展节点(加粗部分，即为选择的迭代路径，最下面为某一个不完全扩展节点，即基有未经访问的子节点，图中未画出。 因为所展示的树上的节点都是访问过的。)；在扩展阶段，根据扩展策略选择其一个未访问过的子节点（如图上加粗部分，在选择阶段是没有的，因为其之前并未被访问，在当前扩展阶段则将其加入树中）；然后，在模拟阶段从这个未访问的子节点开始，采用模拟策略，一直到最终状态，生成结果；最后将这个结果反向对此路径上的所有点更新信息，即完成一次完整的MCTS迭代。
在一般的MCTS算法中，扩展策略与模拟策略采用随机策略。对于选择策略，采取UCB(upper confidenece bound) 或称UCT(upper confidence bound for trees)
其中v'是v的某个子节点， N(v), N(v')分别表示访问节点v和其子节点v'的次数，Q(v') 表示v'获得的所有奖励。那么此公式的第一项表示子节点v'经访问获得的平均奖励。c是调和因子，常数，人工设定（比如1/\sqrt{2}），其作用是调节第二项所占比重。可见第二项随着子节点v'访问次数增加，其值会有所有降低，也可反过来讲，即访问少的子节点，此值会相对高些。综合两项可知，这一策略平衡了利用与探索(exploitatione and exploration)，即有效利用之前经验倾向选择当前的高价值节点，也会兼顾探索，即（第二项）倾向于选择访问次数少的子节点，避免陷入局部最优。
[8]: A Survey ofMonte Carlo Tree Search Methods.
[9]: Świechowski, M., Godlewski, K., Sawicki, B., & Mańdziuk, J. (2021). Monte Carlo Tree Search: A Review of Recent Modifications and Applications.
