leecode: . - 力扣(LeetCode)
题目分类:动态规划、双指针
难度等级:困难
题目描述
给定
n个非负整数表示每个宽度为1的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。示例 1:
输入:height = [0,1,0,2,1,0,1,3,2,1,2,1] 输出:6 解释:上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图,在这种情况下,可以接 6 个单位的雨水(蓝色部分表示雨水)。示例 2:
输入:height = [4,2,0,3,2,5] 输出:9提示:
n == height.length1 <= n <= 2 * 1040 <= height[i] <= 105
题目解读
对于位置 i,能装下多少水呢?
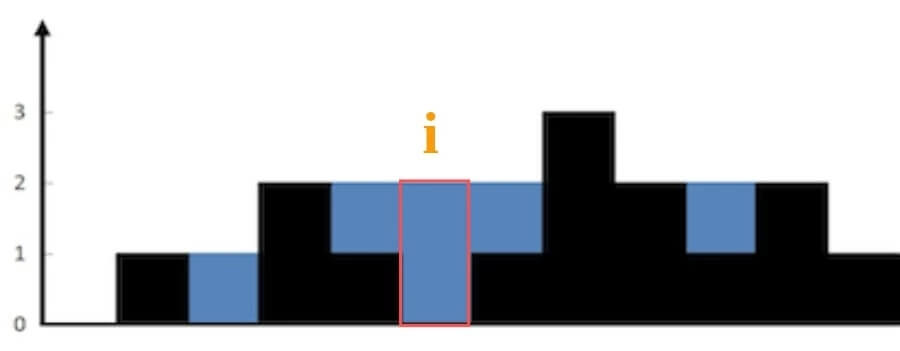
能装 2 格水,因为 height[i] 的高度为 0,而这里最多能盛 2 格水,2-0=2。
为什么位置 i 最多能盛 2 格水呢?因为,位置 i 能达到的水柱高度和其左边的最高柱子、右边的最高柱子有关,我们分别称这两个柱子高度为 l_max 和 r_max;位置 i 最大的水柱高度就是 min(l_max, r_max)。
算法实现
1. 暴力求解
算法设计
从左到右遍历所有元素,计算每一个点i的最大装水量,最后累加
代码实现
int trap(int[] height) {
int n = height.length;
int res = 0;
for (int i = 1; i < n - 1; i++) {
int l_max = 0, r_max = 0;
// 找右边最高的柱子
for (int j = i; j < n; j++)
r_max = Math.max(r_max, height[j]);
// 找左边最高的柱子
for (int j = i; j >= 0; j--)
l_max = Math.max(l_max, height[j]);
// 如果自己就是最高的话,
// l_max == r_max == height[i]
res += Math.min(l_max, r_max) - height[i];
}
return res;
}时间复杂度 O(N^2),空间复杂度 O(1)
2. 备忘录优化
算法设计
之前的暴力解法,不是在每个位置 i 都要计算 r_max 和 l_max 吗?我们直接把结果都提前计算出来,别傻不拉几的每次都遍历,这时间复杂度不就降下来了嘛。
我们开两个数组 r_max 和 l_max 充当备忘录,l_max[i] 表示位置 i 左边最高的柱子高度,r_max[i] 表示位置 i 右边最高的柱子高度。预先把这两个数组计算好,避免重复计算
代码实现
class Solution {
int trap(int[] height) {
if (height.length == 0) {
return 0;
}
int n = height.length;
int res = 0;
// 数组充当备忘录
int[] l_max = new int[n];
int[] r_max = new int[n];
// 初始化 base case
l_max[0] = height[0];
r_max[n - 1] = height[n - 1];
// 从左向右计算 l_max
for (int i = 1; i < n; i++)
l_max[i] = Math.max(height[i], l_max[i - 1]);
// 从右向左计算 r_max
for (int i = n - 2; i >= 0; i--)
r_max[i] = Math.max(height[i], r_max[i + 1]);
// 计算答案
for (int i = 1; i < n - 1; i++)
res += Math.min(l_max[i], r_max[i]) - height[i];
return res;
}
}
时间复杂度降低为 O(N),已经是最优了,但是空间复杂度是 O(N)。
3. 双指针
算法设计
用双指针边走边算,从而节约空间复杂度
代码实现
class Solution {
int trap(int[] height) {
int left = 0, right = height.length - 1;
int l_max = 0, r_max = 0;
int res = 0;
while (left < right) {
l_max = Math.max(l_max, height[left]);
r_max = Math.max(r_max, height[right]);
// res += min(l_max, r_max) - height[i]
if (l_max < r_max) {
res += l_max - height[left];
left++;
} else {
res += r_max - height[right];
right--;
}
}
return res;
}
}






【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 从 HTTP 原因短语缺失研究 HTTP/2 和 HTTP/3 的设计差异
· AI与.NET技术实操系列:向量存储与相似性搜索在 .NET 中的实现
· 基于Microsoft.Extensions.AI核心库实现RAG应用
· Linux系列:如何用heaptrack跟踪.NET程序的非托管内存泄露
· 开发者必知的日志记录最佳实践
· winform 绘制太阳,地球,月球 运作规律
· AI与.NET技术实操系列(五):向量存储与相似性搜索在 .NET 中的实现
· 超详细:普通电脑也行Windows部署deepseek R1训练数据并当服务器共享给他人
· 【硬核科普】Trae如何「偷看」你的代码?零基础破解AI编程运行原理
· 上周热点回顾(3.3-3.9)