引言
常见的数据结构与算法题目,涵盖了数组、链表、栈、队列、二叉树、哈希表、字符串、图、排序和查找等方面的考察点。每个题目都附带有LeetCode的链接,可以点击链接了解更多题目详情
概述
| 类型 | 题目 | 考察点 | 难度 | LeetCode链接 |
|---|---|---|---|---|
| 数组 | 两数之和 | 哈希表、查找 | 简单 | LeetCode 1 |
| 链表 | 合并两个有序链表 | 链表操作、指针 | 简单 | LeetCode 21 |
| 栈 | 有效的括号 | 栈、字符串处理 | 简单 | LeetCode 20 |
| 队列 | 循环队列设计 | 队列、数组 | 中等 | LeetCode 622 |
| 二叉树 | 对称二叉树 | 二叉树递归、对称性判断 | 简单 | LeetCode 101 |
| 哈希表 | 两个数组的交集 II | 哈希表、数组 | 简单 | LeetCode 350 |
| 字符串 | 最长公共前缀 | 字符串处理、前缀判断 | 简单 | LeetCode 14 |
| 图 | 克隆图 | 图的遍历、深拷贝 | 中等 | LeetCode 133 |
| 排序 | 合并排序的数组 | 归并排序、数组操作 | 简单 | LeetCode 88 |
| 查找 | 第 K 个数 | 快速选择、二分查找 | 中等 | LeetCode 215 |
两数之和(LeetCode 1,Easy)
- 标签:哈希表|数组
题目
给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出 和为目标值 target 的那 两个 整数,并返回它们的数组下标。
你可以假设每种输入只会对应一个答案。但是,数组中同一个元素在答案里不能重复出现。
你可以按任意顺序返回答案。
示例 1:
输入:nums = [2,7,11,15], target = 9
输出:[0,1]
解释:因为 nums[0] + nums[1] == 9 ,返回 [0, 1] 。
示例 2:
输入:nums = [3,2,4], target = 6
输出:[1,2]
示例 3:
输入:nums = [3,3], target = 6
输出:[0,1]
提示:
2 <= nums.length <= 104
-109 <= nums[i] <= 109
-109 <= target <= 109
只会存在一个有效答案
原题:LeetCode 1
思路及实现
方式一:暴力解法(不推荐)
思路
最容易想到的方法是枚举数组中的每一个数 x,寻找数组中是否存在 target - x。
当我们使用遍历整个数组的方式寻找 target - x 时,需要注意到每一个位于 x 之前的元素都已经和 x 匹配过,因此不需要再进行匹配。而每一个元素不能被使用两次,所以我们只需要在 x 后面的元素中寻找 target - x。
代码实现
JAVA版本
import java.util.HashMap;
public int[] twoSum(int[] nums, int target) {
int n = nums.length;
for (int i = 0; i < nums.length; i++) { // 遍历数组,从第一个元素开始
for (int j = i + 1; j < nums.length; j++) { // 在当前元素后面的元素中查找与目标值相加等于target的元素
if (nums[i] + nums[j] == target) { // 如果找到了符合条件的元素对
return new int[]{i, j}; // 返回这两个元素的下标
}
}
}
return new int[0]; // 如果没有找到符合条件的元素对,则返回空数组
}
C语言版本
#include <stdio.h>
#include <stdlib.h>
int* twoSum(int* nums, int numsSize, int target, int* returnSize) {
int* result = (int*)malloc(2 * sizeof(int)); // 分配保存结果的内存空间
*returnSize = 0; // 初始化返回结果数组的大小为0,表示没有找到满足条件的元素对
for (int i = 0; i < numsSize; i++) { // 外层循环遍历数组中的每个元素
for (int j = i + 1; j < numsSize; j++) { // 内层循环遍历当前元素后面的每个元素
if (nums[i] + nums[j] == target) { // 检查两个元素的和是否等于目标值
result[0] = i; // 将符合条件的第一个元素的下标存入结果数组的第一个位置
result[1] = j; // 将符合条件的第二个元素的下标存入结果数组的第二个位置
*returnSize = 2; // 更新返回结果数组的大小为2
return result; // 返回结果数组
}
}
}
return result; // 返回结果数组,如果没有找到满足条件的元素对,数组中的元素值均为0
// 注意:需要在适当的时候释放result指向的动态分配内存,以避免内存泄漏
}
python3版本
from typing import List
def twoSum(nums: List[int], target: int) -> List[int]:
result = [] # 用于存储结果的列表
n = len(nums)
for i in range(n): # 外层循环遍历列表中的每个元素
for j in range(i+1, n): # 内层循环遍历当前元素后面的每个元素
if nums[i] + nums[j] == target: # 检查两个元素的和是否等于目标值
result.append(i) # 将符合条件的第一个元素的下标添加到结果列表中
result.append(j) # 将符合条件的第二个元素的下标添加到结果列表中
return result # 返回结果列表
return result # 如果没有找到满足条件的元素对,返回空列表
复杂度分析:
-
时间复杂度分析:O(n^2),其中n为数组nums的长度。这是由于代码使用了两层循环来遍历数组。外层循环将执行n次,而内层循环则将执行(n-1)次、(n-2)次、…、2次、1次,总的执行次数为n * (n-1) / 2,即O(n^2)。
-
空间复杂度分析:O(1),即常数级别的空间复杂度。因为代码只使用了常数个额外变量来存储元素的下标和存储结果的数组。
方式二:哈希表(推荐)
思路
注意到方法一的时间复杂度较高的原因是寻找 target - x 的时间复杂度过高。因此,我们需要一种更优秀的方法,能够快速寻找数组中是否存在目标元素。如果存在,我们需要找出它的索引。
使用哈希表,可以将寻找 target - x 的时间复杂度降低到从 O(N) 降低到 O(1)。
这样我们创建一个哈希表,对于每一个 x,我们首先查询哈希表中是否存在 target - x,然后将 x 插入到哈希表中,即可保证不会让 x 和自己匹配。
下图以[2,7,11,15]为例
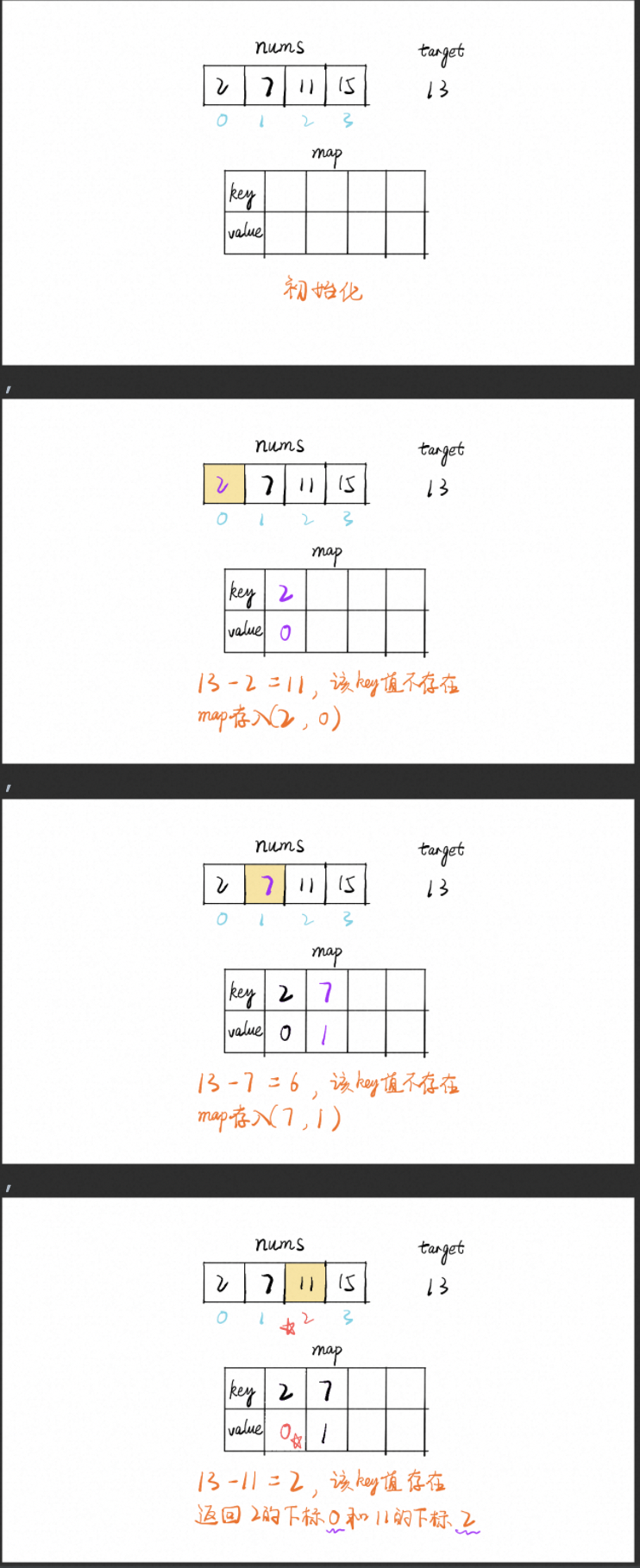
代码实现
JAVA版本
import java.util.HashMap;
class Solution {
public int[] twoSum(int[] nums, int target) {
//key为当前值,value为当前值的位置
HashMap<Integer, Integer> map = new HashMap<>();
for (int i = 0; i < nums.length; i++) {
int complement = target - nums[i]; // 计算差值,即目标值与当前元素的差值
if (map.containsKey(complement)) {
return new int[]{map.get(complement), i}; // 返回HashMap中保存的差值元素的下标和当前元素的下标
}
map.put(nums[i], i); // 将当前元素添加到HashMap中
}
return new int[0]; // 如果没有找到满足条件的元素对,返回空数组
}
}
C语言版本
#include <stdio.h>
#include <stdlib.h>
int* twoSum(int* nums, int numsSize, int target, int* returnSize) {
int* result = (int*)malloc(2 * sizeof(int));
*returnSize = 0;
// 创建哈希表
int hashtable[20001] = {0};
for (int i = 0; i < numsSize; ++i) {
int complement = target - nums[i]; // 计算差值,即目标值与当前元素的差值
// 检查哈希表中是否存在差值
if (complement >= -10000 && complement <= 10000 && hashtable[complement + 10000] != 0) {
result[0] = hashtable[complement + 10000] - 1; // 返回哈希表中保存的差值元素的下标
result[1] = i; // 返回当前元素的下标
*returnSize = 2; // 更新返回结果数组的大小为2
return result;
}
// 将当前元素添加到哈希表中
hashtable[nums[i] + 10000] = i + 1;
}
return result;
}
python3版本
from typing import List
from collections import defaultdict
class Solution:
def twoSum(self, nums: List[int], target: int) -> List[int]:
hashtable = defaultdict(int) # 使用defaultdict来容纳哈希表
for i in range(len(nums)):
complement = target - nums[i] # 计算差值,即目标值与当前元素的差值
if complement in hashtable:
return [hashtable[complement], i] # 返回哈希表中保存的差值元素的下标和当前元素的下标
hashtable[nums[i]] = i # 将当前元素添加到哈希表中
return [] # 如果没有找到满足条件的元素对,返回空列表
复杂度分析:
- 时间复杂度:O(N),其中 N 是数组中的元素数量。对于每一个元素 x,我们可以 O(1) 地寻找 target - x。
- 空间复杂度:O(N),其中 N 是数组中的元素数量。主要为哈希表的开销。
合并两个有序链表(LeetCode 21,Easy)
- 标签:哈希表|数组
题目
将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。
示例 1:
> 输入:l1 = [1,2,4], l2 = [1,3,4] 输出:[1,1,2,3,4,4]
示例 2:输入:l1 = [], l2 = [] 输出:[]
示例 3:
输入:l1 = [], l2 = [0] 输出:[0] 提示:
两个链表的节点数目范围是 [0, 50]
-100 <= Node.val <= 100 l1 和 l2 均按 非递减顺序 排列原题: LeetCode 21
思路及实现
方式一:迭代(推荐)
思路
我们可以用迭代的方法来实现上述算法。当 l1 和 l2 都不是空链表时,判断 l1 和 l2 哪一个链表的头节点的值更小,将较小值的节点添加到结果里,当一个节点被添加到结果里之后,将对应链表中的节点向后移一位
代码实现
Java版本
/**
* Definition for singly-linked list.
* class ListNode {
* int val;
* ListNode next;
* ListNode(int val) {
* this.val = val;
* }
* }
*/
class Solution {
public ListNode mergeTwoLists(ListNode list1, ListNode list2) {
ListNode node = new ListNode(-1); // 创建一个临时节点作为结果链表的头节点
ListNode cur = node;
while (list1 != null && list2 != null) {
if (list1.val < list2.val) {
cur.next = list1; // 将较小节点连接到结果链表
list1 = list1.next; // 移动指针到下一个节点
} else {
cur.next = list2;
list2 = list2.next;
}
cur = cur.next; // 移动当前节点指针到下一个节点
}
if (list1 != null) {
cur.next = list1; // 将剩下的节点连接到结果链表
}
if (list2 != null) {
cur.next = list2;
}
return node.next; // 返回结果链表的头节点
}
}
说明:
创建了一个临时节点作为结果链表的头节点。然后使用cur引用指向当前节点,通过遍历两个链表,比较节点的值,将较小节点连接到结果链表中,并将指针移向下一个节点。最后,将剩下的节点连接到结果链表的末尾。需要注意的是,最后返回的是结果链表的头节点
C语言版本
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* struct ListNode *next;
* };
*/
struct ListNode* mergeTwoLists(struct ListNode* list1, struct ListNode* list2) {
struct ListNode* node = (struct ListNode*)malloc(sizeof(struct ListNode));
node->val = -1; // 创建一个临时节点作为结果链表的头节点
node->next = NULL;
struct ListNode* cur = node;
while (list1 != NULL && list2 != NULL) {
if (list1->val < list2->val) {
cur->next = list1; // 将较小节点连接到结果链表
list1 = list1->next; // 移动指针到下一个节点
} else {
cur->next = list2;
list2 = list2->next;
}
cur = cur->next; // 移动当前节点指针到下一个节点
}
if (list1 != NULL) {
cur->next = list1; // 将剩下的节点连接到结果链表
}
if (list2 != NULL) {
cur->next = list2;
}
struct ListNode* result = node->next; // 指向结果链表的头节点
free(node); // 释放临时节点的内存
return result;
}
说明: 在C语言中使用了头节点,并使用了指针操作来完成。
在算法中,我们创建了一个临时节点作为结果链表的头节点。然后使用cur指针指向当前节点,通过遍历两个链表,比较节点的值,将较小节点连接到结果链表中,并将指针移向下一个节点。最后,将剩下的节点连接到结果链表的末尾。
需要注意的是,最后返回的是结果链表的头节点,使用一个临时节点来保存结果链表的头节点可以简化操作。
在末尾,我们释放了临时节点的内存,以防止内存泄漏。
Python3版本
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution:
def mergeTwoLists(self, list1: ListNode, list2: ListNode) -> ListNode:
node = ListNode(-1) # 创建临时节点作为结果链表的头节点
cur = node
while list1 and list2:
if list1.val < list2.val:
cur.next = list1 # 将较小节点连接到结果链表
list1 = list1.next
else:
cur.next = list2
list2 = list2.next
cur = cur.next
cur.next = list1 or list2 # 将剩下的节点连接到结果链表
return node.next # 返回结果链表的头节点
说明: Python 三元表达式写法 A if x else B ,代表当 x=True 时执行 A ,否则执行 B 。
复杂度分析
- 时间复杂度:O(M+N),M, N分别标识list1和list2的长度
- 空间复杂度: O(1), 节点引用cur,常量级的额外空间
方式二:递归(不推荐)
思路
我们可以如下递归地定义两个链表里的 merge 操作(忽略边界情况,比如空链表等):
情况一 :list1[0]<list2[0],则 list1[0]+merge(list1[1:],list2)
其他情况 :list2[0]+merge(list1,list2[1:])
也就是说,两个链表头部值较小的一个节点与剩下元素的 merge 操作结果合并。
我们直接将以上递归过程建模,同时需要考虑边界情况。
如果 l1 或者 l2 一开始就是空链表 ,那么没有任何操作需要合并,所以我们只需要返回非空链表。否则,我们要判断 l1 和 l2 哪一个链表的头节点的值更小,然后递归地决定下一个添加到结果里的节点。如果两个链表有一个为空,递归结束
代码实现
Java版本
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode() {}
* ListNode(int val) { this.val = val; }
* ListNode(int val, ListNode next) { this.val = val; this.next = next; }
* }
*/
class Solution {
public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
// 如果l1为空,则直接返回l2作为合并后的链表
if (l1 == null) {
return l2;
}
// 如果l2为空,则直接返回l1作为合并后的链表
else if (l2 == null) {
return l1;
}
// 如果l1的值小于l2的值
else if (l1.val < l2.val) {
// 将l1的下一个节点与l2递归地合并
l1.next = mergeTwoLists(l1.next, l2);
return l1; // 返回合并后的链表头节点l1
}
// 如果l2的值小于等于l1的值
else {
// 将l2的下一个节点与l1递归地合并
l2.next = mergeTwoLists(l1, l2.next);
return l2; // 返回合并后的链表头节点l2
}
}
}
说明:
解法提供了递归方式来合并两个有序链表的操作。在算法中,首先处理特殊情况:如果l1为空,则直接返回l2作为合并后的链表;如果l2为空,则直接返回l1作为合并后的链表。接下来,判断l1和l2的值大小关系:如果l1的值小于l2的值,将l1的下一个节点与l2递归地合并,将合并结果作为l1的下一个节点,并返回l1作为合并后的链表头节点;如果l2的值小于等于l1的值,将l2的下一个节点与l1递归地合并,将合并结果作为l2的下一个节点,并返回l2作为合并后的链表头节点。最终,返回合并后的链表头节点。
C语言版本
#include <stdio.h>
#include <stdlib.h>
struct ListNode {
int val;
struct ListNode *next;
};
struct ListNode* mergeTwoLists(struct ListNode* l1, struct ListNode* l2) {
// 如果l1为空,则直接返回l2作为合并后的链表
if (l1 == NULL) {
return l2;
}
// 如果l2为空,则直接返回l1作为合并后的链表
else if (l2 == NULL) {
return l1;
}
// 如果l1的值小于l2的值
else if (l1->val < l2->val) {
// 将l1的下一个节点与l2递归地合并
l1->next = mergeTwoLists(l1->next, l2);
return l1; // 返回合并后的链表头节点l1
}
// 如果l2的值小于等于l1的值
else {
// 将l2的下一个节点与l1递归地合并
l2->next = mergeTwoLists(l1, l2->next);
return l2; // 返回合并后的链表头节点l2
}
}
说明:
在算法中,首先处理特殊情况:如果l1为空,则直接返回l2作为合并后的链表;如果l2为空,则直接返回l1作为合并后的链表。接下来,判断l1和l2的值的大小关系:如果l1的值小于l2的值,将l1的下一个节点与l2递归地合并,将合并结果作为l1的下一个节点,并返回l1作为合并后的链表头节点;如果l2的值小于等于l1的值,将l2的下一个节点与l1递归地合并,将合并结果作为l2的下一个节点,并返回l2作为合并后的链表头节点。最终,返回合并后的链表头节点。
Python3版本
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution:
def mergeTwoLists(self, l1: ListNode, l2: ListNode) -> ListNode:
if not l1: # 如果l1为空,则直接返回l2
return l2
elif not l2: # 如果l2为空,则直接返回l1
return l1
elif l1.val < l2.val: # 如果l1的值小于l2的值
l1.next = self.mergeTwoLists(l1.next, l2) # 递归地将l1的下一个节点与l2合并
return l1
else:
l2.next = self.mergeTwoLists(l1, l2.next) # 递归地将l2的下一个节点与l1合并
return l2
复杂度分析
- 时间复杂度:O(n+m),其中 n 和 m 分别为两个链表的长度。因为每次调用递归都会去掉 l1 或者 l2 的头节点(直到至少有一个链表为空),函数 mergeTwoList 至多只会递归调用每个节点一次。因此,时间复杂度取决于合并后的链表长度,即 O(n+m)。
- 空间复杂度:O(n+m),其中 n 和 m 分别为两个链表的长度。递归调用 mergeTwoLists 函数时需要消耗栈空间,栈空间的大小取决于递归调用的深度。结束递归调用时 mergeTwoLists 函数最多调用 n+m 次,因此空间复杂度为 O(n+m)。
小结
递归和迭代都可以用来解决将两个有序链表合并的问题。下面对比一下递归和迭代的解法特点:
| 递归解法 | 迭代解法 | |
|---|---|---|
| 优点 | 简洁,易于理解和实现 | 不涉及函数递归调用,避免递归开销和栈溢出问题 |
| 缺点 | 可能产生多个函数调用,涉及函数调用开销和栈溢出问题 | 需要使用额外变量保存当前节点,增加代码复杂性 |
| 时间复杂度 | O(m+n),其中m和n分别是两个链表的长度 | O(m+n),其中m和n分别是两个链表的长度 |
| 空间复杂度 | O(m+n),其中m和n分别是两个链表的长度 | O(1) |
在实际应用中,如果链表较长,特别是超过系统栈的容量,采用迭代解法更为安全。而对于简短的链表,递归解法更为简洁和直观。
有效的括号(LeetCode 20,Easy)
- 标签:栈、字符串处理
题目
给定一个只包括 ‘(’,‘)’,‘{’,‘}’,‘[’,‘]’ 的字符串 s ,判断字符串是否有效。
有效字符串需满足:
左括号必须用相同类型的右括号闭合。 左括号必须以正确的顺序闭合。 每个右括号都有一个对应的相同类型的左括号。
示例 1:
输入:s = “()” 输出:true
示例 2:输入:s = “()[]{}” 输出:true
示例 3:输入:s = “(]” 输出:false
提示:
1 <= s.length <= 104 s 仅由括号 ‘()[]{}’ 组成
思路及实现
方式一:栈(推荐)
思路
判断括号的有效性可以使用「栈」这一数据结构来解决。
代码实现
Java版本
import java.util.Stack;
// leetcode submit region begin(Prohibit modification and deletion)
class Solution {
public boolean isValid(String s) {
Stack<Character> stack = new Stack<>(); // 创建一个栈用于存储左括号字符
for (int i = 0; i < s.length(); i++) {
char c = s.charAt(i);
if (c == '(' || c == '[' || c == '{') {
stack.push(c); // 如果是左括号字符,将其压入栈中
} else {
if (stack.isEmpty()) {
return false; // 如果栈为空,说明缺少左括号,返回false
}
char top = stack.pop(); // 弹出栈顶元素
if (c == ')' && top != '(') {
return false; // 如果当前字符是右括号且与栈顶元素不匹配,返回false
}
if (c == ']' && top != '[') {
return false;
}
if (c == '}' && top != '{') {
return false;
}
}
}
return stack.isEmpty(); // 最后判断栈是否为空,如果为空说明每个左括号都有匹配的右括号,则返回true,否则返回false
}
}
// leetcode submit region end(Prohibit modification and deletion)
说明:
使用栈来判断给定的字符串中的括号是否匹配。先创建一个空栈,然后遍历字符串中的每个字符。如果是左括号字符,则压入栈中;如果是右括号字符,则与栈顶元素进行匹配。匹配成功则继续遍历,匹配失败则返回false。最后判断栈是否为空,如果为空则说明所有的括号都被匹配,返回true;否则,说明还有未匹配的括号,返回false
C++版本(由于C语言需要自己实现栈较为繁琐,此处使用C++)
#include <iostream>
#include <stack>
#include <string>
using namespace std;
bool isValid(string s) {
stack<char> stk; // 创建一个栈用于存储左括号字符
for (char c : s) {
if (c == '(' || c == '[' || c == '{') {
stk.push(c); // 如果是左括号字符,将其压入栈中
} else {
if (stk.empty()) {
return false; // 如果栈为空,说明缺少左括号,返回false
}
char top = stk.top(); /* 获取栈顶元素 */
stk.pop(); // 弹出栈顶元素
if (c == ')' && top != '(') {
return false; // 如果当前字符是右括号且与栈顶元素不匹配,返回false
}
if (c == ']' && top != '[') {
return false;
}
if (c == '}' && top != '{') {
return false;
}
}
}
return stk.empty(); // 最后判断栈是否为空,如果为空说明每个左括号都有匹配的右括号,则返回true,否则返回false
}
说明:
使用C++的标准库来实现栈,判断给定的字符串中的括号是否匹配。首先创建一个stack用于存储左括号字符。然后遍历字符串中的每个字符,如果是左括号字符,则将其压入栈中;如果是右括号字符,则与栈顶元素进行匹配。匹配成功则继续遍历,匹配失败则返回false。最后判断栈是否为空,如果为空则说明所有的括号都被匹配,返回true;否则,说明还有未匹配的括号,返回false。
Python3版本
class Solution:
def isValid(self, s: str) -> bool:
stack = [] # 创建一个栈用于存储左括号字符
brackets = {'(': ')', '[': ']', '{': '}'}
for char in s:
if char in brackets.keys(): # 如果是左括号字符,将其压入栈中
stack.append(char)
elif char in brackets.values(): # 如果是右括号字符
if not stack: # 如果栈为空,说明缺少左括号,返回False
return False
top = stack.pop() # 弹出栈顶元素
if char != brackets[top]: # 如果当前字符与栈顶元素不匹配,返回False
return False
return len(stack) == 0 # 判断栈是否为空,为空说明每个左括号都有匹配的右括号
说明:
创建一个列表作为栈来判断给定的字符串中的括号是否匹配。首先定义了一个字典brackets,用来存储左括号和右括号的对应关系。然后遍历字符串中的每个字符,如果是左括号字符,则将其压入栈中;如果是右括号字符,则和栈顶元素进行匹配。匹配成功则继续遍历,匹配失败则返回False。最后判断栈是否为空,如果为空则说明所有的括号都被匹配,返回True;否则,说明还有未匹配的括号,返回False
复杂度分析
- 时间复杂度:O(n),其中 n 是字符串 s 的长度。
- 空间复杂度:O(n),其中n为字符串的长度。在最坏情况下,所有的字符都是左括号,需要将其全部入栈,占用了O(n) 的空间。
这个算法具有线性时间复杂度和线性空间复杂度。
循环队列设计(LeetCode 622,Medium)
- 标签:队列、数组
题目
设计你的循环队列实现。 循环队列是一种线性数据结构,其操作表现基于 FIFO(先进先出)原则并且队尾被连接在队首之后以形成一个循环。它也被称为“环形缓冲器”。
循环队列的一个好处是我们可以利用这个队列之前用过的空间。在一个普通队列里,一旦一个队列满了,我们就不能插入下一个元素,即使在队列前面仍有空间。但是使用循环队列,我们能使用这些空间去存储新的值。
你的实现应该支持如下操作:
MyCircularQueue(k): 构造器,设置队列长度为 k 。
Front: 从队首获取元素。如果队列为空,返回 -1 。
Rear: 获取队尾元素。如果队列为空,返回 -1 。
enQueue(value): 向循环队列插入一个元素。如果成功插入则返回真。
deQueue(): 从循环队列中删除一个元素。如果成功删除则返回真。
isEmpty(): 检查循环队列是否为空。
isFull(): 检查循环队列是否已满。
示例:
MyCircularQueue circularQueue = new MyCircularQueue(3); // 设置长度为 3
circularQueue.enQueue(1); // 返回 true
circularQueue.enQueue(2); // 返回 true
circularQueue.enQueue(3); // 返回 true
circularQueue.enQueue(4); // 返回 false,队列已满
circularQueue.Rear(); // 返回 3
circularQueue.isFull(); // 返回 true
circularQueue.deQueue(); // 返回 true
circularQueue.enQueue(4); // 返回 true
circularQueue.Rear(); // 返回 4
提示:
所有的值都在 0 至 1000 的范围内;
操作数将在 1 至 1000 的范围内;
请不要使用内置的队列库。
原题:[LeetCode 622](https://leetcode-cn.com/problems/design-circular-queue/)
思路及实现
方式一:数组(不推荐)
思路
我们可以通过一个数组进行模拟,通过操作数组的索引构建一个虚拟的首尾相连的环。在循环队列结构中,设置一个队尾 rear 与队首 front,且大小固定,结构如下图所示:
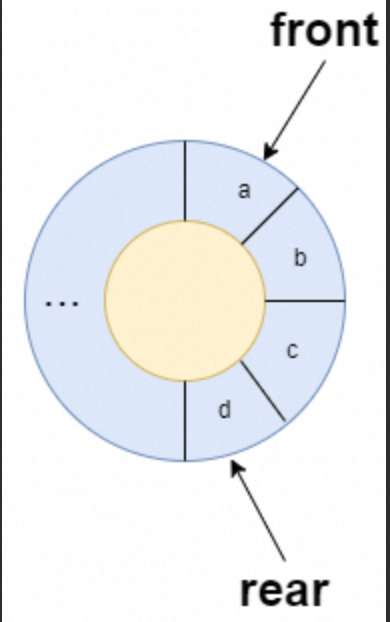
在循环队列中,当队列为空,可知 front=rear;
而当所有队列空间全占满时,也有 front=rear。
为了区别这两种情况,假设队列使用的数组有 capacity 个存储空间,则此时规定循环队列最多只能有capacity−1 个队列元素,当循环队列中只剩下一个空存储单元时,则表示队列已满。
根据以上可知,队列判空的条件是 front=rear,而队列判满的条件是 front=(rear+1)modcapacity。
对于一个固定大小的数组,只要知道队尾 rear 与队首 front,即可计算出队列当前的长度:(rear−front+capacity)modcapacity
循环队列的属性如下:
- elements:一个固定大小的数组,用于保存循环队列的元素。
- capacity:循环队列的容量,即队列中最多可以容纳的元素数量。
- front:队列首元素对应的数组的索引。
- rear:队列尾元素对应的索引的下一个索引。
循环队列的接口方法如下:
MyCircularQueue(int k): 初始化队列,同时base 数组的空间初始化大小为 k+1。front,rear 全部初始化为 0。
enQueue(int value):在队列的尾部插入一个元素,并同时将队尾的索引 rear 更新为 (rear+1)modcapacity。
deQueue():从队首取出一个元素,并同时将队首的索引 front 更新为 (front+1)modcapacity。
Front():返回队首的元素,需要检测队列是否为空。
Rear():返回队尾的元素,需要检测队列是否为空。
isEmpty():检测队列是否为空,根据之前的定义只需判断 rear 是否等于 front。
isFull():检测队列是否已满,根据之前的定义只需判断 front 是否等于 (rear+1)modcapacity。
代码实现
Java版本
class MyCircularQueue {
private int front; // 队头指针
private int rear; // 队尾指针
private int capacity; // 队列容量
private int[] elements; // 存储队列元素的数组
public MyCircularQueue(int k) {
capacity = k + 1; // 设置队列容量,需要额外留一个空位用于判断队满的条件
elements = new int[capacity]; // 创建存储队列元素的数组
rear = front = 0; // 初始化队头和队尾指针
}
public boolean enQueue(int value) {
if (isFull()) {
return false; // 如果队列已满,无法入队,返回false
}
elements[rear] = value; // 将元素放入队尾
rear = (rear + 1) % capacity; // 队尾指针后移一位,通过取模实现循环
return true;
}
public boolean deQueue() {
if (isEmpty()) {
return false; // 如果队列为空,无法出队,返回false
}
front = (front + 1) % capacity; // 队头指针后移一位,通过取模实现循环
return true;
}
public int Front() {
if (isEmpty()) {
return -1; // 如果队列为空,返回-1
}
return elements[front]; // 返回队头元素
}
public int Rear() {
if (isEmpty()) {
return -1; // 如果队列为空,返回-1
}
return elements[(rear - 1 + capacity) % capacity]; // 返回队尾元素,通过(rear-1+capacity)%capacity实现循环
}
public boolean isEmpty() {
return rear == front; // 队头指针等于队尾指针时,队列为空
}
public boolean isFull() {
return (rear + 1) % capacity == front; // 队头指针的下一个位置等于队尾指针时,队列为满
}
}
说明:
代码实现了一个循环队列类MyCircularQueue,使用数组来存储队列的元素,并使用front和rear两个指针来指示队头和队尾的位置。在构造方法MyCircularQueue中,初始化capacity为k+1,由于要留出一个空位来判断队满的条件,因此数组的长度为capacity。在入队方法enQueue中,首先判断队列是否已满,如果已满则无法入队,返回false;否则将元素放入队尾,并将rear指针循环到下一个位置。在出队方法deQueue中,首先判断队列是否为空,如果为空则无法出队,返回false;否则将front指针循环到下一个位置。在Front方法中,如果队列为空则返回-1,否则返回front指针所指位置的元素。在Rear方法中,如果队列为空则返回-1,否则返回rear指针的前一个位置(通过(rear-1+capacity)%capacity来实现循环)。isEmpty方法用于判断队列是否为空,即判断rear与front是否相等。isFull方法用于判断队列是否已满,即判断(rear+1)%capacity是否等于front。这个代码中使用成员变量来存储队列的状态和数据,方法通过操作这些成员变量来实现对队列的操作。方法的返回值为布尔型,用于表示操作是否成功,而不是抛出异常来处理异常情况。
C语言版本
typedef struct {
int front; // 队头指针
int rear; // 队尾指针
int capacity; // 队列容量
int* elements; // 存储队列元素的数组
} MyCircularQueue;
MyCircularQueue* myCircularQueueCreate(int k) {
MyCircularQueue* obj = (MyCircularQueue*)malloc(sizeof(MyCircularQueue)); // 分配队列结构体的内存空间
obj->capacity = k + 1; // 设置队列容量,需要额外留一个空位用于判断队满的条件
obj->front = obj->rear = 0; // 初始化队头和队尾指针为0
obj->elements = (int*)malloc(sizeof(int) * obj->capacity); // 创建存储队列元素的数组
return obj;
}
bool myCircularQueueEnQueue(MyCircularQueue* obj, int value) {
if ((obj->rear + 1) % obj->capacity == obj->front) {
return false; // 如果队列已满,无法入队,返回false
}
obj->elements[obj->rear] = value; // 将元素放入队尾
obj->rear = (obj->rear + 1) % obj->capacity; // 队尾指针后移一位,通过取模实现循环
return true;
}
bool myCircularQueueDeQueue(MyCircularQueue* obj) {
if (obj->rear == obj->front) {
return false; // 如果队列为空,无法出队,返回false
}
obj->front = (obj->front + 1) % obj->capacity; // 队头指针后移一位,通过取模实现循环
return true;
}
int myCircularQueueFront(MyCircularQueue* obj) {
if (obj->rear == obj->front) {
return -1; // 如果队列为空,返回-1
}
return obj->elements[obj->front]; // 返回队头元素
}
int myCircularQueueRear(MyCircularQueue* obj) {
if (obj->rear == obj->front) {
return -1; // 如果队列为空,返回-1
}
return obj->elements[(obj->rear - 1 + obj->capacity) % obj->capacity]; // 返回队尾元素,通过(rear-1+capacity)%capacity实现循环
}
bool myCircularQueueIsEmpty(MyCircularQueue* obj) {
return obj->rear == obj->front; // 队头指针等于队尾指针时,队列为空
}
bool myCircularQueueIsFull(MyCircularQueue* obj) {
return (obj->rear + 1) % obj->capacity == obj->front; // 队头指针的下一个位置等于队尾指针时,队列为满
}
void myCircularQueueFree(MyCircularQueue* obj) {
free(obj->elements); // 释放存储队列元素的数组内存空间
free(obj); // 释放队列结构体内存空间
}
说明:使用结构体MyCircularQueue来存储队列的状态和数据。结构体中包括front和rear两个指针,capacity队列容量,以及存储队列元素的elements数组。
Python3版本
class MyCircularQueue:
def __init__(self, k: int):
self.front = self.rear = 0 # 初始化队头和队尾指针
self.elements = [0] * (k + 1) # 创建一个长度为k+1的数组来存储元素,留出一个空位作为判断队满的条件
def enQueue(self, value: int) -> bool:
if self.isFull(): # 如果队满,无法入队,返回False
return False
self.elements[self.rear] = value # 将元素放入队尾
self.rear = (self.rear + 1) % len(self.elements) # 队尾指针后移一位
return True
def deQueue(self) -> bool:
if self.isEmpty(): # 如果队空,无法出队,返回False
return False
self.front = (self.front + 1) % len(self.elements) # 队头指针后移一位
return True
def Front(self) -> int:
return -1 if self.isEmpty() else self.elements[self.front] # 如果队空,返回-1;否则返回队头元素
def Rear(self) -> int:
return -1 if self.isEmpty() else self.elements[(self.rear - 1) % len(self.elements)] # 如果队空,返回-1;否则返回队尾元素
def isEmpty(self) -> bool:
return self.rear == self.front # 队头指针等于队尾指针时,队列为空
def isFull(self) -> bool:
return (self.rear + 1) % len(self.elements) == self.front # 队头指针的下一位等于队尾指针时,队列为满
说明:
代码实现了一个循环队列类MyCircularQueue,使用一个数组来存储队列元素,并用队头和队尾指针来指示队列的位置。在__init__方法中,初始化队头和队尾指针,并创建一个长度为k+1的数组来存储元素,其中k为传入的参数。在isFull方法中,通过判断队头指针的下一位是否等于队尾指针来判断队列是否为满。在isEmpty方法中,通过判断队头指针是否等于队尾指针来判断队列是否为空。enQueue方法实现元素的入队操作,先判断队列是否为满,如果为满则无法入队,返回False;否则将元素放入队尾,并将队尾指针后移一位。deQueue方法实现元素的出队操作,先判断队列是否为空,如果为空则无法出队,返回False;否则将队头指针后移一位。Front方法返回队列的队头元素,如果队列为空则返回-1。Rear方法返回队列的队尾元素,如果队列为空则返回-1。
复杂度分析
- 时间复杂度:初始化和每项操作的时间复杂度均为 O(1)。
- 空间复杂度:O(k),其中 k 为给定的队列元素数目。
方式二:链表(推荐)
思路
我们同样可以用链表实现队列,用链表实现队列则较为简单,因为链表可以在 O(1) 时间复杂度完成插入与删除。入队列时,将新的元素插入到链表的尾部;出队列时,将链表的头节点返回,并将头节点指向下一个节点。
循环队列的属性如下:
- head:链表的头节点,队列的头节点。
- tail:链表的尾节点,队列的尾节点。
- capacity:队列的容量,即队列可以存储的最大元素数量。
- size:队列当前的元素的数量。
代码实现
Java
class MyCircularQueue {
private ListNode head; // 队头节点
private ListNode tail; // 队尾节点
private int capacity; // 队列容量
private int size; // 当前队列的元素个数
public MyCircularQueue(int k) {
capacity = k;
size = 0;
}
public boolean enQueue(int value) {
if (isFull()) {
return false; // 如果队列已满,无法入队,返回false
}
ListNode node = new ListNode(value);
if (head == null) {
head = tail = node; // 如果队列为空,设置头部和尾部节点为新节点
} else {
tail.next = node; // 将新节点添加到尾部
tail = node; // 更新尾部节点
}
size++; // 元素个数加1
return true;
}
public boolean deQueue() {
if (isEmpty()) {
return false; // 如果队列为空,无法出队,返回false
}
head = head.next; // 将头部节点后移一位,实现出队操作
size--; // 元素个数减1
return true;
}
public int Front() {
if (isEmpty()) {
return -1; // 如果队列为空,返回-1
}
return head.val; // 返回头部节点的值
}
public int Rear() {
if (isEmpty()) {
return -1; // 如果队列为空,返回-1
}
return tail.val; // 返回尾部节点的值
}
public boolean isEmpty() {
return size == 0; // 如果元素个数为0,队列为空
}
public boolean isFull() {
return size == capacity; // 如果元素个数等于队列容量,队列已满
}
}
class ListNode {
int val;
ListNode next;
public ListNode(int val) {
this.val = val;
}
}
说明:
MyCircularQueue 类实现了一个循环队列,使用了链表来存储队列的元素。在构造方法 MyCircularQueue 中,初始化了队头节点 head 和队尾节点 tail 为 null,队列的容量 capacity
为传入的参数 k,当前队列元素个数 size 初始化为 0。enQueue 方法用于入队操作,首先判断队列是否已满,如果已满,则无法入队,返回 false。创建一个新的节点
node,如果队列为空,则将 head 和 tail 指针指向新节点;否则,将新节点添加到尾部,并更新 tail 指向新节点。元素个数
size 加 1,并返回 true 表示入队成功。
C语言
typedef struct {
struct ListNode *head; // 队头指针
struct ListNode *tail; // 队尾指针
int capacity; // 队列容量
int size; // 当前队列的元素个数
} MyCircularQueue;
MyCircularQueue* myCircularQueueCreate(int k) {
MyCircularQueue *obj = (MyCircularQueue *)malloc(sizeof(MyCircularQueue)); // 创建队列结构体并分配内存空间
obj->capacity = k; // 设置队列容量
obj->size = 0; // 当前队列元素个数为0
obj->head = obj->tail = NULL; // 初始化队头和队尾指针为 NULL
return obj;
}
bool myCircularQueueEnQueue(MyCircularQueue* obj, int value) {
if (obj->size >= obj->capacity) {
return false; // 如果队列已满,无法入队,返回 false
}
struct ListNode *node = (struct ListNode *)malloc(sizeof(struct ListNode)); // 创建新节点并分配内存空间
node->val = value; // 设置节点的值
node->next = NULL; // 初始化节点的下一个指针为 NULL
if (!obj->head) {
obj->head = obj->tail = node; // 如果队列为空,设置头部和尾部指针为新节点
} else {
obj->tail->next = node; // 将新节点添加到尾部
obj->tail = node; // 更新尾部指针
}
obj->size++; // 当前队列元素个数加1
return true;
}
bool myCircularQueueDeQueue(MyCircularQueue* obj) {
if (obj->size == 0) {
return false; // 如果队列为空,无法出队,返回 false
}
struct ListNode *node = obj->head; // 保存当前头部节点
obj->head = obj->head->next; // 头部指针后移一位,实现出队操作
obj->size--; // 当前队列元素个数减1
free(node); // 释放出队节点的内存
return true;
}
int myCircularQueueFront(MyCircularQueue* obj) {
if (obj->size == 0) {
return -1; // 如果队列为空,返回 -1
}
return obj->head->val; // 返回头部节点的值
}
int myCircularQueueRear(MyCircularQueue* obj) {
if (obj->size == 0) {
return -1; // 如果队列为空,返回 -1
}
return obj->tail->val; // 返回尾部节点的值
}
bool myCircularQueueIsEmpty(MyCircularQueue* obj) {
return obj->size == 0; // 如果当前队列元素个数为0,队列为空
}
bool myCircularQueueIsFull(MyCircularQueue* obj) {
return obj->size == obj->capacity; // 如果当前队列元素个数等于队列容量,队列已满
}
void myCircularQueueFree(MyCircularQueue* obj) {
for (struct ListNode *curr = obj->head; curr;) { // 遍历整个队列,从头部开始
struct ListNode *node = curr; // 保存当前节点
curr = curr->next; // 移动到下一个节点
free(node); // 释放当前节点的内存
}
free(obj); // 释放队列结构体的内存
}
说明:
使用了结构体来存储队列的状态和数据。在 myCircularQueueCreate 函数中,初始化了队列的容量 capacity 为传入的参数 k,当前队列元素个数 size为 0,并将队头 head 和队尾 tail 指针初始化为 NULL。
Python3
class ListNode:
def __init__(self, val=0, next=None):
self.val = val
self.next = next
class MyCircularQueue:
def __init__(self, k: int):
self.head = self.tail = None # 队头和队尾指针,用于指向队列的头部和尾部
self.capacity = k # 队列容量
self.size = 0 # 当前队列中的元素个数
def enQueue(self, value: int) -> bool:
if self.isFull(): # 如果队列已满,无法入队,返回False
return False
node = ListNode(value) # 创建一个新节点
if self.head is None: # 如果队列为空,设置头部和尾部指针为新节点
self.head = node
self.tail = node
else:
self.tail.next = node # 将新节点添加到尾部
self.tail = node # 更新尾部指针
self.size += 1 # 元素个数加1
return True
def deQueue(self) -> bool:
if self.isEmpty(): # 如果队列为空,无法出队,返回False
return False
self.head = self.head.next # 将头部指针后移一位,实现出队操作
self.size -= 1 # 元素个数减1
return True
def Front(self) -> int:
return -1 if self.isEmpty() else self.head.val # 如果队列为空,返回-1;否则返回头部节点的值
def Rear(self) -> int:
return -1 if self.isEmpty() else self.tail.val # 如果队列为空,返回-1;否则返回尾部节点的值
def isEmpty(self) -> bool:
return self.size == 0 # 如果元素个数为0,队列为空
def isFull(self) -> bool:
return self.size == self.capacity # 如果元素个数等于队列容量,队列已满
说明: 使用链表来存储队列的元素。ListNode是节点结构体,用于表示队列中的每个节点。
MyCircularQueue类的初始化方法__init__中,初始化队头和队尾指针为None,队列容量为k,当前队列的元素个数为0。
enQueue
方法用于入队操作,首先判断队列是否已满,如果已满则无法入队,返回False。创建一个新节点,如果队列为空,设置头部和尾部指针为新节点;否则,将新节点添加到队尾,并更新尾部指针。元素个数加1,并返回True
表示入队成功。
复杂度分析
- 时间复杂度:初始化和每项操作的时间复杂度均为 O(1)。
- 空间复杂度:O(k),其中 k 为给定的队列元素数目。
数组VS链表
| 方面 | 数组 | 链表 |
|---|---|---|
| 存储方式 | 连续的内存空间 | 非连续的内存空间 |
| 插入和删除操作 | O(n) | O(1) |
| 随机访问 | O(1) | O(n) |
| 内存效率 | 较高(不需要额外指针空间) | 较低(需要额外指针空间) |
| 大小变化 | 需要重新分配内存空间 | 可以动态变化 |
| 实现复杂性 | 相对简单 | 相对复杂 |
对称二叉树(LeetCode 101,Easy)
- 标签:二叉树递归、对称性判断
题目
给你一个二叉树的根节点 root , 检查它是否轴对称。
示例 1:
输入:root = [1,2,2,3,4,4,3] 输出:true 示例 2:
输入:root = [1,2,2,null,3,null,3] 输出:false
提示:
树中节点数目在范围 [1, 1000] 内
-100 <= Node.val <= 100进阶:你可以运用递归和迭代两种方法解决这个问题吗?
原题: LeetCode 101
思路及实现
方式一:递归(推荐)
思路
乍一看无从下手,但用递归其实很好解决。
根据题目的描述,镜像对称,就是左右两边相等,也就是左子树和右子树是相当的。
注意这句话,左子树和右子相等,也就是说要递归的比较左子树和右子树。
我们将根节点的左子树记做 left,右子树记做 right。比较 left 是否等于 right,不等的话直接返回就可以了。
如果相当,比较 left 的左节点和 right 的右节点,再比较 left 的右节点和 right 的左节点
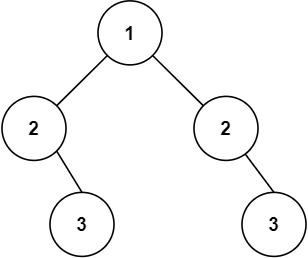
比如看下面这两个子树(他们分别是根节点的左子树和右子树),能观察到这么一个规律:
左子树 2 的左孩子 == 右子树 2 的右孩子
左子树 2 的右孩子 == 右子树 2 的左孩子
根据上面信息可以总结出递归函数的两个终止条件:
- left 和 right 不等,或者 left 和 right 都为空
- 递归的比较 left,left 和 right.right,递归比较
left,right 和 right.left
代码实现
Java版本
class Solution {
public boolean isSymmetric(TreeNode root) {
if (root == null) {
return true; // 如果根节点为null,即空树,视为对称二叉树,返回true
}
return isMirror(root.left, root.right); // 调用isMirror方法判断左子树和右子树是否对称
}
private boolean isMirror(TreeNode left, TreeNode right) {
if (left == null && right == null) {
return true; // 如果左子树和右子树都为null,也视为对称,返回true
}
if (left == null || right == null) {
return false; // 如果左子树和右子树只有一个为null,视为不对称,返回false
}
return left.val == right.val && isMirror(left.left, right.right) && isMirror(left.right, right.left);
// 如果左子树和右子树的值相等,且同时满足左子树的左子树和右子树的右子树对称,
// 以及左子树的右子树和右子树的左子树对称,则视为对称,返回true;否则,返回false
}
}
说明:
isSymmetric方法是该函数的入口,接收一个二叉树的根节点作为参数。首先判断根节点是否为null,如果是,即空树,视为对称二叉树,返回true。否则,调用isMirror 方法来判断左子树和右子树是否对称。isMirror方法是递归判断左右子树是否对称的函数。首先判断左子树和右子树是否都为null,如果是,即均为空树,视为对称,返回true。然后判断左子树和右子树中只有一个为null的情况,即一个为空树一个不为空树,视为不对称,返回false。最后,判断左子树的值和右子树的值是否相等,并且同时递归判断左子树的左子树和右子树的右子树是否对称,以及递归判断左子树的右子树和右子树的左子树是否对称。只有全部满足才视为对称,返回true;否则,返回false。
C语言版本
#include <stdbool.h>
/*struct TreeNode {
int val;
struct TreeNode *left;
struct TreeNode *right;
};
*/
bool isMirror(struct TreeNode *left, struct TreeNode *right);
bool isSymmetric(struct TreeNode *root) {
if (root == NULL) {
return true; // 如果根节点为NULL,即空树,视为对称二叉树,返回true
}
return isMirror(root->left, root->right); // 调用isMirror函数判断左子树和右子树是否对称
}
bool isMirror(struct TreeNode *left, struct TreeNode *right) {
if (left == NULL && right == NULL) {
return true; // 如果左子树和右子树都为NULL,也视为对称,返回true
}
if (left == NULL || right == NULL) {
return false; // 如果左子树和右子树只有一个为NULL,视为不对称,返回false
}
return (left->val == right->val) && isMirror(left->left, right->right) && isMirror(left->right, right->left);
// 如果左子树和右子树的值相等,并且同时满足左子树的左子树和右子树的右子树对称,
// 以及左子树的右子树和右子树的左子树对称,则视为对称,返回true;否则,返回false
}
Python3版本
class Solution:
def isSymmetric(self, root: TreeNode) -> bool:
if root is None:
return True # 如果根节点为空,返回True,空树被认为是对称的
return self.isMirror(root.left, root.right)
def isMirror(self, left: TreeNode, right: TreeNode) -> bool:
if left is None and right is None:
return True # 如果左子树和右子树都为空,认为是对称的
if left is None or right is None:
return False # 如果左子树和右子树只有一个为空,不对称
return left.val == right.val and self.isMirror(left.left, right.right) and self.isMirror(left.right, right.left)
# 比较左子树的左子树和右子树的右子树,以及左子树的右子树和右子树的左子树,满足条件才认为是对称的
# 假设定义了TreeNode类,包含val、left和right属性
class TreeNode:
def __init__(self, val: int = 0, left: TreeNode = None, right: TreeNode = None):
self.val = val
self.left = left
self.right = right
说明:代码中使用了 TreeNode 类来定义树节点,包含 val、left 和 right 属性。其中 val 存储节点的值,left 和
right 存储左子树和右子树的引用。
复杂度分析
- 时间复杂度:O(n),其中 n 表示树的节点数。
- 空间复杂度:O(n),递归调用的栈空间最多为树的高度。
方式二:队列(迭代)
思路
回想下递归的实现:
当两个子树的根节点相等时,就比较:
左子树的 left 和 右子树的 right,这个比较是用递归实现的。
现在我们改用队列来实现,思路如下:
首先从队列中拿出两个节点(left 和 right)比较:
将 left 的 left 节点和 right 的 right 节点放入队列
将 left 的 right 节点和 right 的 left 节点放入队列
代码实现
Java版本
//leetcode submit region begin(Prohibit modification and deletion)
import java.util.LinkedList;
class Solution {
public boolean isSymmetric(TreeNode root) {
if (root == null) {
return false; // 根节点为空,不算对称
}
if (root.left == null && root.right == null) {
return true; // 左右子树都为空,算对称
}
LinkedList<TreeNode> queue = new LinkedList(); // 使用队列来保存待比较的节点
queue.add(root.left);
queue.add(root.right);
while (queue.size() > 0) {
TreeNode left = queue.removeFirst();
TreeNode right = queue.removeFirst();
// 只要两个节点都为空,继续循环;两者有一个为空,返回false
if (left == null && right == null) {
continue;
}
if (left == null || right == null) {
return false;
}
// 判断两个节点的值是否相等
if (left.val != right.val) {
return false;
}
// 将左节点的左子节点和右节点的右子节点放入队列
queue.add(left.left);
queue.add(right.right);
// 将左节点的右子节点和右节点的左子节点放入队列
queue.add(left.right);
queue.add(right.left);
}
return true;
}
}
//leetcode submit region end(Prohibit modification and deletion)
说明:
这段代码使用迭代方法判断二叉树是否对称。在 isSymmetric 方法中,首先判断根节点是否为空,如果为空,返回 false,表示不对称。然后,如果根节点的左右子树都为空,返回 true,表示对称(只有一个元素的case)。
接下来,创建一个队列 queue,并将根节点的左子节点和右子节点加入队列。然后进入循环,每次从队列中取出两个节点进行比较。在比较过程中,只要两个节点均为空,继续循环;如果只有一个节点为空,返回
false,表示不对称。然后,比较两个节点的值是否相等,如果不相等,返回 false。将左节点的左子节点和右节点的右子节点放入队列,用于后续比较。同时,将左节点的右子节点和右节点的左子节点放入队列,也用于后续比较。
当队列为空时,表示所有节点都已比较完毕,没有发现不对称的情况,返回 true,表示对称。
这段代码使用了迭代方法,利用队列存储待比较的节点,逐层按顺序比较,避免了递归方法的额外栈空间开销。
C语言版本
// leetcode submit region begin(Prohibit modification and deletion)
#include <stdbool.h>
struct TreeNode {
int val;
struct TreeNode *left;
struct TreeNode *right;
};
bool isSymmetric(struct TreeNode* root) {
if (root == NULL) {
return false; // 根节点为空,不算对称
}
struct TreeNode* queue[10000]; // 使用队列来保存待比较的节点
int front = 0, rear = 0;
queue[rear++] = root->left;
queue[rear++] = root->right;
while (rear != front) {
struct TreeNode* left = queue[front++];
struct TreeNode* right = queue[front++];
// 只要两个节点都为空,继续循环;两者有一个为空,返回false
if (left == NULL && right == NULL) {
continue;
}
if (left == NULL || right == NULL) {
return false;
}
// 判断两个节点的值是否相等
if (left->val != right->val) {
return false;
}
// 将左节点的左子节点和右节点的右子节点放入队列
queue[rear++] = left->left;
queue[rear++] = right->right;
// 将左节点的右子节点和右节点的左子节点放入队列
queue[rear++] = left->right;
queue[rear++] = right->left;
}
return true;
}
//leetcode submit region end(Prohibit modification and deletion)
说明:
这段代码使用C语言实现了迭代方法来判断二叉树是否对称。在 isSymmetric 函数中,首先判断根节点是否为空,如果为空,返回 false,表示不对称。
创建一个队列 queue,使用数组来保存待比较的节点。使用 front 和 rear 变量分别表示队首和队尾的索引。
将根节点的左子节点和右子节点依次加入队列 queue。
然后进入循环,每次从队列中取出两个节点进行比较。
在比较过程中,只要两个节点均为空,继续循环;如果只有一个节点为空,返回
false,表示不对称。然后,比较两个节点的值是否相等,如果不相等,返回 false。将左节点的左子节点和右节点的右子节点放入队列,用于后续比较。同时,将左节点的右子节点和右节点的左子节点放入队列,也用于后续比较。
当队列为空时,表示所有节点都已比较完毕,没有发现不对称的情况,返回 true,表示对称。
这段代码使用了迭代方法,利用数组队列方式存储待比较的节点,逐个按序比较,避免了递归方法的额外栈空间开销。
Python3版本
class Solution:
def isSymmetric(self, root: TreeNode) -> bool:
if root is None:
return False # 根节点为空,不算对称
queue = []
queue.append(root.left)
queue.append(root.right)
while queue:
left = queue.pop(0)
right = queue.pop(0)
if left is None and right is None:
continue # 只要两个节点都为空,继续循环
if left is None or right is None:
return False # 两者有一个为空,返回False,不对称
if left.val != right.val:
return False # 节点值不相等,不对称
queue.append(left.left) # 左节点的左子节点入队列
queue.append(right.right) # 右节点的右子节点入队列
queue.append(left.right) # 左节点的右子节点入队列
queue.append(right.left) # 右节点的左子节点入队列
return True # 队列为空,所有节点比较完毕,对称
说明:(基础说明可查看java或者c的实现)
在函数参数的类型注解中,使用了 TreeNode 类型来标注 root 参数的类型。
使用了 is 运算符来判断节点是否为 None。is 运算符比较的是对象的身份标识,用于判断对象是否是同一个对象。这里用它来判断节点是否为None。
使用了列表 queue 来实现队列的功能,通过 append() 方法将节点加入队列的尾部,通过 pop(0)
方法来从队列的头部取出节点。Python的列表可以很方便地实现队列的功能。
复杂度分析
- 时间复杂度:O(n),其中 n 表示树的节点数。在最坏情况下,需要遍历树的所有节点。
- 空间复杂度:O(n),最坏情况下,队列中需要存储树的一层节点,所以空间复杂度与树的高度有关。在最坏情况下,树的高度为 n/2,因此空间复杂度为 O(n)。
综合来看,这个算法的时间复杂度和空间复杂度都是 O(n),其中 n 表示树的节点数。算法的性能随着节点数的增加而线性增长。
两个数组的交集 II(LeetCode 350,Easy)
- 标签:哈希表、数组
题目
给你两个整数数组 nums1 和 nums2 ,请你以数组形式返回两数组的交集。返回结果中每个元素出现的次数,
应与元素在两个数组中都出现的次数一致(如果出现次数不一致,则考虑取较小值)。可以不考虑输出结果的顺序。
示例 1:
输入:nums1 = [1,2,2,1], nums2 = [2,2]
输出:[2,2]
示例 2:
输入:nums1 = [4,9,5], nums2 = [9,4,9,8,4]
输出:[4,9]
提示:
1 <= nums1.length, nums2.length <= 1000
0 <= nums1[i], nums2[i] <= 1000
进阶:
如果给定的数组已经排好序呢?你将如何优化你的算法?
如果 nums1 的大小比 nums2 小,哪种方法更优?
如果 nums2 的元素存储在磁盘上,内存是有限的,并且你不能一次加载所有的元素到内存中,你该怎么办?
思路及实现
方式一:哈希表
思路
由于同一个数字在两个数组中都可能出现多次,因此需要用哈希表存储每个数字出现的次数。对于一个数字,其在交集中出现的次数等于该数字在两个数组中出现次数的最小值。
首先遍历第一个数组,并在哈希表中记录第一个数组中的每个数字以及对应出现的次数,然后遍历第二个数组,对于第二个数组中的每个数字,如果在哈希表中存在这个数字,则将该数字添加到答案,并减少哈希表中该数字出现的次数。
为了降低空间复杂度,首先遍历较短的数组并在哈希表中记录每个数字以及对应出现的次数,然后遍历较长的数组得到交集。
代码实现
Java版本
class Solution {
public int[] intersect(int[] nums1, int[] nums2) {
Map<Integer, Integer> numMap = new HashMap<>();
List<Integer> res = new ArrayList<>();
// 遍历 nums1 数组,将元素及其出现次数存储在哈希表中
for (int num : nums1) {
numMap.put(num, numMap.getOrDefault(num, 0) + 1);
}
// 遍历 nums2 数组,检查每个元素是否在哈希表中出现
// 如果出现,将该元素添加到结果集中,并将哈希表中的对应出现次数减1
for (int num : nums2) {
if (numMap.containsKey(num) && numMap.get(num) > 0) {
res.add(num);
numMap.put(num, numMap.get(num) - 1);
}
}
// 将结果集转换为数组输出
int[] result = new int[res.size()];
for (int i = 0; i < res.size(); i++) {
result[i] = res.get(i);
}
return result;
}
}
说明:
使用哈希表来求解两个数组的交集,并将结果集转换为数组输出。首先创建一个哈希表 numMap 来存储第一个数组 nums1 中每个元素及其出现的次数。 创建一个列表 res 来存储交集结果。 遍历
nums2 数组,对于每个元素 num,检查其是否在哈希表 numMap 中出现且出现次数大于 0。 如果满足条件,则将该元素加入结果集res 中,并将哈希表中对应出现次数减 1。 将结果集 res 转换为数组输出。 返回最终的结果数组。tips优化空间:
哈希表 numMap 只用来存储 nums1 中的元素及其出现次数,而不是存储两个数组的交集。可以减少额外空间的使用。
结果集 res 使用列表存储交集结果,并在最后将其转换为数组输出。 优化空间后的复杂度分析与之前相同,时间复杂度为 O(m +
n),空间复杂度为 O(min(m, n))。其中 m 和 n 分别表示两个输入数组的长度。
C语言版本
#include <stdio.h>
#include <stdlib.h>
/**
* 返回两个整数中的较小值
*/
int min(int a, int b) {
return a < b ? a : b;
}
int* intersect(int* nums1, int nums1Size, int* nums2, int nums2Size, int* returnSize) {
// 使用哈希表来存储nums1中每个元素及其出现的次数
int* numMap = (int*) malloc(sizeof(int) * 1001);
for (int i = 0; i < nums1Size; i++) {
numMap[nums1[i]]++;
}
int* res = (int*) malloc(sizeof(int) * min(nums1Size, nums2Size)); // 结果集使用动态分配的数组来存储
int resSize = 0; // 结果集的大小
// 遍历nums2数组,检查每个元素在哈希表中是否存在
// 如果存在且对应出现次数大于0,则加入结果集,并将对应出现次数减1
for (int i = 0; i < nums2Size; i++) {
if (numMap[nums2[i]] > 0) {
res[resSize++] = nums2[i];
numMap[nums2[i]]--;
}
}
*returnSize = resSize; // 将结果集的大小赋给返回值
free(numMap); // 释放动态分配的内存
return res; // 返回结果集数组的指针
}
说明:
使用数组 numMap 来存储 nums1 数组中每个元素及其出现的次数,数组下标表示元素值。 遍历 nums2 数组,对于每个元素nums2[i],如果 numMap[nums2[i]] 大于 0,则将 nums2[i] 添加到结果集 res 中,并将
numMap[nums2[i]] 减 1。 使用动态分配的数组 res 来存储交集结果,动态分配的内存大小为较小的数组大小
min(nums1Size, nums2Size)。 将结果集的大小 resSize 赋给
returnSize,即将结果集的大小返回给调用函数。 使用 free() 函数释放动态分配的内存。
Python3版本
class Solution:
def intersect(self, nums1, nums2):
# 使用哈希表来存储nums1中每个元素及其出现的次数
numMap = {}
for num in nums1:
numMap[num] = numMap.get(num, 0) + 1
res = []
# 遍历nums2数组,检查每个元素在哈希表中是否存在
# 如果存在且对应出现次数大于0,则加入结果集,并将对应出现次数减1
for num in nums2:
if num in numMap and numMap[num] > 0:
res.append(num)
numMap[num] -= 1
return res
说明:
使用字典 numMap 来存储 nums1 数组中每个元素及其出现的次数。 遍历 nums2 数组,对于每个元素 num,如果num 在 numMap 中存在且对应出现次数大于 0,则将 num 添加到结果集 res 中,并将 numMap[num] 减 1。返回结果集 res。
复杂度分析
- 时间复杂度:O(max(m, n)),其中 m 和 n 分别表示两个输入数组的长度。需要遍历两个数组并对哈希表进行操作,哈希表操作的时间复杂度是 O(1),因此总时间复杂度与两个数组的长度和呈线性关系。
- 空间复杂度:O(min(m, n)),表示两个输入数组中较小的那个数组的长度
方式二:排序 + 双指针
思路
如果两个数组是有序的,则可以使用双指针的方法得到两个数组的交集。
首先对两个数组进行排序,然后使用两个指针遍历两个数组。
初始时,两个指针分别指向两个数组的头部。每次比较两个指针指向的两个数组中的数字,如果两个数字不相等,则将指向较小数字的指针右移一位,如果两个数字相等,将该数字添加到答案,并将两个指针都右移一位。当至少有一个指针超出数组范围时,遍历结束。
代码实现
Java版本
class Solution {
public int[] intersect(int[] nums1, int[] nums2) {
// 对两个数组进行排序
Arrays.sort(nums1);
Arrays.sort(nums2);
// 获取两个数组的长度
int length1 = nums1.length, length2 = nums2.length;
// 创建结果数组,长度为两个数组中较小的长度
int[] intersection = new int[Math.min(length1, length2)];
// 初始化指针和结果数组的索引
int index1 = 0, index2 = 0, index = 0;
// 双指针法求交集
while (index1 < length1 && index2 < length2) {
if (nums1[index1] < nums2[index2]) {
index1++; // nums1的元素较小,移动nums1的指针
} else if (nums1[index1] > nums2[index2]) {
index2++; // nums2的元素较小,移动nums2的指针
} else {
// 相等,加入结果数组,同时移动两个指针和结果数组的索引
intersection[index] = nums1[index1];
index1++;
index2++;
index++;
}
}
// 返回交集结果数组,利用Arrays.copyOfRange()截取结果数组的有效部分
return Arrays.copyOfRange(intersection, 0, index);
}
}
说明:
首先,对两个输入的数组 nums1 和 nums2 进行排序,这里使用了 Arrays.sort() 方法。时间复杂度为
O(nlogn),其中 n 分别表示两个数组的长度。 初始化指针 index1 和 index2 分别指向数组 nums1 和 nums2
的起始位置,同时初始化结果数组的索引 index 为 0。 创建结果数组 intersection,长度为两个数组长度较小的那个。
使用双指针法进行比较: 如果 nums1[index1] 小于 nums2[index2],说明 nums1 的元素较小,将 index1
向后移动。 如果 nums1[index1] 大于 nums2[index2],说明 nums2 的元素较小,将 index2 向后移动。
如果 nums1[index1] 等于 nums2[index2],说明找到了一个交集元素,将该元素加入结果数组 intersection
中,并将两个指针和结果数组的索引都向后移动。 当有一个指针越界时,表示已经遍历完其中一个数组,此时得到的结果数组即为两个数组的交集。
最后,利用 Arrays.copyOfRange() 方法截取结果数组 intersection 的有效部分(0 到
index-1),并返回新的数组作为输出。
C语言版本
#include <stdlib.h>
int cmp(const void *a, const void *b) {
return (*(int *)a - *(int *)b);
}
int *intersect(int *nums1, int nums1Size, int *nums2, int nums2Size, int *returnSize) {
// 对两个数组进行排序
qsort(nums1, nums1Size, sizeof(int), cmp);
qsort(nums2, nums2Size, sizeof(int), cmp);
// 创建结果数组,长度为两个数组中较小的大小
int *intersection = (int *)malloc(sizeof(int) * (nums1Size < nums2Size ? nums1Size : nums2Size));
// 初始化指针和结果数组索引
int index1 = 0, index2 = 0, index = 0;
// 双指针法求交集
while (index1 < nums1Size && index2 < nums2Size) {
if (nums1[index1] < nums2[index2]) {
index1++; // nums1的元素较小,移动nums1的指针
} else if (nums1[index1] > nums2[index2]) {
index2++; // nums2的元素较小,移动nums2的指针
} else {
// 相等,加入结果数组,同时移动两个指针和结果数组的索引
intersection[index] = nums1[index1];
index1++;
index2++;
index++;
}
}
// 返回交集结果数组的大小
*returnSize = index;
return intersection;
}
说明:
使用qsort()函数对输入的两个数组nums1和nums2进行排序。这里使用了自定义的比较函数cmp()来指定排序规则。排序后,两个数组中的元素将按照从小到大的顺序排列。
创建一个结果数组intersection,长度为两个数组中较小的那个。使用动态内存分配函数malloc()来分配存储交集结果所需的内存空间。
初始化两个指针index1和index2,分别指向数组nums1和nums2的起始位置。同时,初始化结果数组的索引index为0。
使用双指针法进行比较遍历: 如果nums1[index1]小于nums2[index2],说明nums1的元素较小,将index1向后移动。
如果nums1[index1]大于nums2[index2],说明nums2的元素较小,将index2向后移动。
如果nums1[index1]等于nums2[index2],说明找到了一个交集元素,将该元素加入结果数组intersection中,并将两个指针和结果数组的索引都向后移动。
当有一个指针越界时,表示已经遍历完其中一个数组,此时得到的结果数组即为两个数组的交集。
使用指针returnSize来记录交集结果数组的大小。 返回交集结果数组intersection的指针。
Python3版本
class Solution:
def intersect(self, nums1: List[int], nums2: List[int]) -> List[int]:
# 对两个数组进行排序
nums1.sort()
nums2.sort()
# 获取两个数组的长度
length1, length2 = len(nums1), len(nums2)
# 创建一个空列表来存储交集结果
intersection = list()
# 初始化两个指针
index1 = index2 = 0
# 双指针法求交集
while index1 < length1 and index2 < length2:
if nums1[index1] < nums2[index2]:
index1 += 1
elif nums1[index1] > nums2[index2]:
index2 += 1
else:
# 相等,加入结果列表,同时移动两个指针
intersection.append(nums1[index1])
index1 += 1
index2 += 1
# 返回交集结果列表
return intersection
说明:
对输入的两个数组nums1和nums2进行排序,这里使用了Python内置的sort()方法,能在原地排序。
创建一个空列表intersection来存储交集结果。
使用双指针法进行比较,分别初始化index1和index2为0,它们分别指向数组nums1和nums2的起始位置。
遍历两个数组,比较当前指针位置上的元素大小。 如果nums1[index1]小于nums2[index2],则index1向右移动。
如果nums1[index1]大于nums2[index2],则index2向右移动。
如果nums1[index1]等于nums2[index2],则找到一个交集元素,加入结果列表intersection中,并同时移动两个指针。
当有一个指针越界时,表示已经遍历完其中一个数组,那么结果列表intersection中存储的就是两个数组的交集。
返回交集结果列表intersection。
复杂度分析
- 时间复杂度:O(mlogm+nlogn),其中 m 和 n 分别是两个数组的长度。对两个数组进行排序的时间复杂度是 O(mlogm+nlogn),遍历两个数组的时间复杂度是 O(m+n),因此总时间复杂度是 O(mlogm+nlogn)。
- 空间复杂度:O(min(m,n)),其中 m 和 n 分别是两个数组的长度。为返回值创建一个数组 intersection,其长度为较短的数组的长度。不过在 C++ 中,我们可以直接创建一个 vector,不需要把答案临时存放在一个额外的数组中,所以这种实现的空间复杂度为 O(1)。
最长公共前缀(LeetCode 14,Easy)
- 标签:字符串处理、前缀判断
题目
编写一个函数来查找字符串数组中的最长公共前缀。
如果不存在公共前缀,返回空字符串 ""。
示例 1:
输入:strs = ["flower","flow","flight"]
输出:"fl"
示例 2:
输入:strs = ["dog","racecar","car"]
输出:""
解释:输入不存在公共前缀。
提示:
1 <= strs.length <= 200
0 <= strs[i].length <= 200
strs[i] 仅由小写英文字母组成
原题:LeetCode 14
思路及实现
方式一:横向扫描
思路


代码实现
Java
class Solution {
public String longestCommonPrefix(String[] strs) {
// 如果字符串数组为空或者长度为0,则返回空字符串
if (strs == null || strs.length == 0) {
return "";
}
// 将第一个字符串作为前缀进行初始化
String prefix = strs[0];
// 数组中字符串的数量
int count = strs.length;
// 遍历字符串数组,依次求取最长公共前缀
for (int i = 1; i < count; i++) {
prefix = longestCommonPrefix(prefix, strs[i]);
// 如果最长公共前缀为空,则可以提前结束循环
if (prefix.length() == 0) {
break;
}
}
// 返回最长公共前缀
return prefix;
}
// 求取两个字符串的最长公共前缀
public String longestCommonPrefix(String str1, String str2) {
// 获取两个字符串的最小长度
int length = Math.min(str1.length(), str2.length());
// 初始化索引
int index = 0;
// 遍历两个字符串,找到最长公共前缀的结束索引
while (index < length && str1.charAt(index) == str2.charAt(index)) {
index++;
}
// 返回最长公共前缀
return str1.substring(0, index);
}
}
说明:
首先,通过判断字符串数组strs是否为空或长度为0,来确定是否存在最长公共前缀。如果数组为空或长度为0,则直接返回空字符串。
将字符串数组中的第一个字符串作为初始化的最长公共前缀prefix。
使用一个循环遍历剩余的字符串,依次计算最长公共前缀。在每次循环中,调用longestCommonPrefix()方法,将当前最长公共前缀prefix和当前遍历的字符串进行比较,更新最长公共前缀。
如果最长公共前缀为空字符串,则说明不存在公共前缀,无需继续循环,直接跳出。 最后,返回最长公共前缀prefix。
longestCommonPrefix()方法是一个内部方法,用于找到两个字符串str1和str2的最长公共前缀。
首先,获取两个字符串的最小长度length。 初始化索引index为0。
遍历两个字符串,比较对应位置的字符是否相等,直到遇到不相等的字符或到达较短字符串的末尾。
最后,返回前缀部分的字符串,即str1中的前index个字符。
C语言版本
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
char* longestCommonPrefix(char** strs, int strsSize) {
// 如果字符串数组为空或者长度为0,则返回空字符串
if (strs == NULL || strsSize == 0)
return "";
// 将第一个字符串作为初始的最长公共前缀
char* prefix = strs[0];
// 遍历数组剩余的字符串,更新最长公共前缀
for (int i = 1; i < strsSize; i++) {
prefix = lcp(prefix, strs[i]);
// 如果最长公共前缀为空,则跳出循环
if (prefix[0] == '\0')
break;
}
return prefix;
}
说明:
longestCommonPrefix() 函数用于找到字符串数组 strs 中的最长公共前缀。
首先,判断字符串数组是否为空或长度为0,如果是,则直接返回空字符串。 将数组的第一个字符串作为初始的最长公共前缀 prefix。
遍历数组剩余的字符串,调用 lcp() 函数计算当前字符串与当前最长公共前缀的公共前缀,并更新最长公共前缀 prefix。
如果最长公共前缀为空字符串,则无需继续遍历,跳出循环。 返回最长公共前缀 prefix。 lcp() 函数用于找到两个字符串 str1 和str2 的最长公共前缀。 获取两个字符串的最小长度 length。 初始化索引 index 为0。
遍历两个字符串,比较对应位置的字符是否相等,直到遇到不相等的字符或到达较短字符串的末尾。 创建一个新的字符串来存储最长公共前缀commonPrefix。
使用 strncpy() 函数从 str1 复制 index 个字符到 commonPrefix 中。 在
commonPrefix 的末尾添加字符串结束符 ‘\0’。 返回最长公共前缀 commonPrefix。
Python3版本
class Solution:
def longestCommonPrefix(self, strs: List[str]) -> str:
# 如果字符串数组为空,则返回空字符串
if not strs:
return ""
# 将数组的第一个字符串作为初始的最长公共前缀
prefix, count = strs[0], len(strs)
# 遍历数组剩余的字符串,更新最长公共前缀
for i in range(1, count):
prefix = self.lcp(prefix, strs[i])
# 如果最长公共前缀为空,则跳出循环
if not prefix:
break
return prefix
# 求取两个字符串的最长公共前缀
def lcp(self, str1, str2):
# 获取两个字符串的最小长度
length, index = min(len(str1), len(str2)), 0
# 遍历两个字符串,找到最长公共前缀的结束索引
while index < length and str1[index] == str2[index]:
index += 1
# 返回最长公共前缀
return str1[:index]
说明:
longestCommonPrefix()方法是一个类方法,用于找到字符串数组strs中的最长公共前缀。
首先,判断字符串数组是否为空,如果为空,则直接返回空字符串。 将数组的第一个字符串作为初始的最长公共前缀 prefix。
获取数组中的字符串数量 count。 使用一个循环遍历剩余的字符串,调用 lcp()
方法来计算当前字符串与当前最长公共前缀的公共前缀,并更新最长公共前缀 prefix。 如果最长公共前缀为空字符串,则无需继续遍历,跳出循环。
返回最长公共前缀 prefix。 lcp() 方法是一个类方法,用于找到两个字符串 str1 和 str2 的最长公共前缀。
获取两个字符串的最小长度 length。 初始化索引 index 为0。
遍历两个字符串,比较对应位置的字符是否相等,直到遇到不相等的字符或到达较短字符串的末尾。 返回前缀部分的字符串,即 str1 中的前
index 个字符。
复杂度分析
- 时间复杂度:O(mn),其中 m 是字符串数组中的字符串的平均长度,n 是字符串的数量。最坏情况下,字符串数组中的每个字符串的每个字符都会被比较一次。
- 空间复杂度:O(1)。使用的额外空间复杂度为常数。
方式二:纵向扫描
思路
方法一是横向扫描,依次遍历每个字符串,更新最长公共前缀。另一种方法是纵向扫描。纵向扫描时,从前往后遍历所有字符串的每一列,比较相同列上的字符是否相同,如果相同则继续对下一列进行比较,如果不相同则当前列不再属于公共前缀,当前列之前的部分为最长公共前缀。

代码实现
Java
class Solution {
public String longestCommonPrefix(String[] strs) {
// 如果字符串数组为空或者长度为0,直接返回空字符串
if (strs == null || strs.length == 0) {
return "";
}
// 获取第一个字符串的长度和数组的长度
int length = strs[0].length();
int count = strs.length;
// 遍历第一个字符串的每个字符
for (int i = 0; i < length; i++) {
char c = strs[0].charAt(i);
// 遍历剩余的字符串进行比较
for (int j = 1; j < count; j++) {
// 如果当前字符已经超过了某个字符串的长度,或者当前字符不等于其他字符串对应位置的字符,返回前缀部分
if (i == strs[j].length() || strs[j].charAt(i) != c) {
return strs[0].substring(0, i);
}
}
}
// 返回第一个字符串作为最长公共前缀
return strs[0];
}
}
说明:
longestCommonPrefix() 方法用于寻找字符串数组 strs 中的最长公共前缀。
如果字符串数组为空或长度为0,直接返回空字符串。 获取第一个字符串的长度和字符串数组的长度。 遍历第一个字符串的每个字符。 获取当前字符
c,用来与其他字符串的对应位置字符进行比较。 遍历剩余的字符串,依次比较当前字符和其他字符串对应位置的字符。
如果当前字符已经超过了某个字符串的长度,或者当前字符不等于其他字符串对应位置的字符,返回前缀部分,即第一个字符串的从索引0到当前位置的子串。
返回第一个字符串作为最长公共前缀,因为该字符串是其他字符串的公共前缀。
C语言版本
在这里插入代码片
Python
在这里插入代码片
复杂度分析
- 时间复杂度:O(mn),其中 m 是字符串数组中的字符串的平均长度,n 是字符串的数量。最坏情况下,字符串数组中的每个字符串的每个字符都会被比较一次。
- 空间复杂度:O(1)。使用的额外空间复杂度为常数。
方式三:纵向扫描
思路


代码实现
Java版本
class Solution {
public String longestCommonPrefix(String[] strs) {
// 如果字符串数组为空或者长度为0,直接返回空字符串
if (strs == null || strs.length == 0) {
return "";
} else {
return longestCommonPrefix(strs, 0, strs.length - 1);
}
}
// 递归函数,用于求取指定范围内字符串数组的最长公共前缀
public String longestCommonPrefix(String[] strs, int start, int end) {
// 如果范围内只有一个字符串,则直接返回该字符串作为最长公共前缀
if (start == end) {
return strs[start];
} else {
// 计算范围中间索引
int mid = (end - start) / 2 + start;
// 求取左半部分和右半部分的最长公共前缀
String lcpLeft = longestCommonPrefix(strs, start, mid);
String lcpRight = longestCommonPrefix(strs, mid + 1, end);
// 返回左半部分和右半部分的最长公共前缀的公共前缀
return commonPrefix(lcpLeft, lcpRight);
}
}
// 求取两个字符串的最长公共前缀的公共前缀
public String commonPrefix(String lcpLeft, String lcpRight) {
// 获取最小长度
int minLength = Math.min(lcpLeft.length(), lcpRight.length());
// 对比两个字符串的字符,找到不相等的位置,返回前缀部分
for (int i = 0; i < minLength; i++) {
if (lcpLeft.charAt(i) != lcpRight.charAt(i)) {
return lcpLeft.substring(0, i);
}
}
// 返回最小长度范围内的字符串,即最长公共前缀
return lcpLeft.substring(0, minLength);
}
}
说明:
longestCommonPrefix() 方法是递归函数,用于求取指定范围内字符串数组 strs 的最长公共前缀。
如果范围内只有一个字符串,则直接返回该字符串作为最长公共前缀。 否则,计算范围中间索引 mid。 调用递归函数
longestCommonPrefix() 分别求取左半部分和右半部分的最长公共前缀:lcpLeft 和 lcpRight。
返回左半部分和右半部分的最长公共前缀的公共前缀,即调用 commonPrefix() 函数。 commonPrefix()
方法用于求取两个字符串 lcpLeft 和 lcpRight 的最长公共前缀的公共前缀。 获取两个字符串的长度的最小值作为最小长度minLength。 逐个字符比较两个字符串的对应位置的字符,找到不相等的位置,返回当前位置前的子串作为最长公共前缀的公共前缀。
如果没有找到不相等的位置,返回最小长度范围内的字符串,即最长公共前缀。
C语言版本
#include <stdio.h>
#include <string.h>
// 函数声明
char* longestCommonPrefix(char** strs, int strsSize);
/*
* 获取两个字符串的最长公共前缀
* 参数: str1 - 字符串1, str2 - 字符串2
* 返回值: 最长公共前缀的指针
*/
char* commonPrefix(char* str1, char* str2);
/*
* 获取字符串数组中的最长公共前缀
* 参数: strs - 字符串数组, strsSize - 字符串数组的长度
* 返回值: 最长公共前缀的指针
*/
char* longestCommonPrefix(char** strs, int strsSize) {
// 如果字符串数组为空或者长度为0,直接返回空字符串
if (strs == NULL || strsSize == 0) {
return "";
}
// 将第一个字符串作为初始的最长公共前缀
char* prefix = strs[0];
// 遍历剩余的字符串
for (int i = 1; i < strsSize; i++) {
// 更新最长公共前缀为当前遍历的字符串与最长公共前缀的公共前缀
prefix = commonPrefix(prefix, strs[i]);
// 如果最长公共前缀为空,说明不存在公共前缀,直接跳出循环
if (strlen(prefix) == 0) {
break;
}
}
return prefix;
}
/*
* 获取两个字符串的最长公共前缀的公共前缀
* 参数: str1 - 字符串1, str2 - 字符串2
* 返回值: 最长公共前缀的指针
*/
char* commonPrefix(char* str1, char* str2) {
int length1 = strlen(str1);
int length2 = strlen(str2);
int index = 0;
while (index < length1 && index < length2 && str1[index] == str2[index]) {
index++;
}
// 创建新的字符串,存储公共前缀
char* result = (char*)malloc((index + 1) * sizeof(char));
strncpy(result, str1, index);
result[index] = '\0'; // 末尾添加结束符
return result;
}
说明:
longestCommonPrefix()函数用于找到字符串数组中的最长公共前缀。
在函数中,首先判断字符串数组是否为空或长度为0。如果是,则直接返回空字符串。 将字符串数组的第一个字符串作为初始的最长公共前缀prefix。
使用一个循环遍历剩余的字符串,分别与当前最长公共前缀进行比较,更新最长公共前缀。 如果最长公共前缀为空字符串,说明不存在公共前缀,跳出循环。
返回最长公共前缀prefix的指针。 commonPrefix()函数用于找到两个字符串的最长公共前缀的公共前缀。
在函数中,通过计算两个字符串的长度,初始化索引index为0。
使用一个循环比较两个字符串的对应位置字符,直到遇到不相等的字符或其中一个字符串的结尾。
创建一个新的字符数组result,用于存储公共前缀部分。 使用strncpy()函数将公共前缀部分复制到result中。
在result末尾添加结束符\0。 返回公共前缀result的指针。
请注意,使用malloc()动态分配了内存空间来存储结果字符串,因此在使用完毕后,记得使用free()函数释放它。
Python3版本
class Solution:
def longestCommonPrefix(self, strs: List[str]) -> str:
# 定义递归函数,用于求取字符串数组中指定范围内的最长公共前缀
def lcp(start, end):
# 如果范围中只有一个字符串,则直接返回该字符串作为最长公共前缀
if start == end:
return strs[start]
# 分治法,将范围划分为两部分,分别求取左右两部分的最长公共前缀
mid = (start + end) // 2
lcpLeft, lcpRight = lcp(start, mid), lcp(mid + 1, end)
# 找到左右两部分最长公共前缀的最小长度
minLength = min(len(lcpLeft), len(lcpRight))
# 在最小长度范围内逐个字符比较
for i in range(minLength):
if lcpLeft[i] != lcpRight[i]:
# 遇到第一个不相等的字符,返回前缀部分
return lcpLeft[:i]
# 返回最小长度范围内的最长公共前缀
return lcpLeft[:minLength]
# 如果字符串数组为空,则返回空字符串
return "" if not strs else lcp(0, len(strs) - 1)
说明:
使用分治法,将指定范围划分为左右两部分,分别求取它们的最长公共前缀。 计算中间索引 mid。 调用 lcp()
函数求取左半部分的最长公共前缀 lcpLeft。 调用 lcp() 函数求取右半部分的最长公共前缀 lcpRight。
找到左右两部分最长公共前缀的最小长度。 在最小长度范围内逐个字符比较左右两部分的对应位置字符。
如果遇到第一个不相等的字符,返回当前位置前的子串作为最长公共前缀。 返回最小长度范围内的最长公共前缀。 如果字符串数组为空,则返回空字符串。
否则,调用 lcp() 函数,传入起始索引0和结束索引 len(strs) - 1,求取整个字符串数组的最长公共前缀。
longestCommonPrefix() 方法是主函数,用于启动递归过程并处理边界情况。lcp() 函数是一个内部递归函数,用于求取字符串数组中指定范围内的最长公共前缀
复杂度分析
- 时间复杂度:O(mn),其中 m 是字符串数组中的字符串的平均长度,n 是字符串的数量。时间复杂度的递推式是 T(n)=2⋅T(2n )+O(m),通过计算可得 T(n)=O(mn)。
- 空间复杂度:O(mlogn),其中 m 是字符串数组中的字符串的平均长度,n 是字符串的数量。空间复杂度主要取决于递归调用的层数,层数最大为 logn,每层需要 m 的空间存储返回结果。
方式四:二分查找
显然,最长公共前缀的长度不会超过字符串数组中的最短字符串的长度。用 minLength 表示字符串数组中的最短字符串的长度,则可以在 [0,minLength] 的范围内通过二分查找得到最长公共前缀的长度。每次取查找范围的中间值 mid,判断每个字符串的长度为 mid 的前缀是否相同,如果相同则最长公共前缀的长度一定大于或等于 mid,如果不相同则最长公共前缀的长度一定小于 mid,通过上述方式将查找范围缩小一半,直到得到最长公共前缀的长度。

代码实现
Java版本
class Solution {
public String longestCommonPrefix(String[] strs) {
// 如果字符串数组为空或长度为0,直接返回空字符串
if (strs == null || strs.length == 0) {
return "";
}
// 获取字符串数组中最短字符串的长度
int minLength = Integer.MAX_VALUE;
for (String str : strs) {
minLength = Math.min(minLength, str.length());
}
// 使用二分查找的思路来查找最长公共前缀
int low = 0, high = minLength;
while (low < high) {
// 取中间位置
int mid = (high - low + 1) / 2 + low;
// 判断中间位置的前缀是否是公共前缀
if (isCommonPrefix(strs, mid)) {
// 如果是,更新 low,继续查找右半部分
low = mid;
} else {
// 如果不是,更新 high,继续查找左半部分
high = mid - 1;
}
}
// 返回最长公共前缀
return strs[0].substring(0, low);
}
// 判断指定长度前缀是否是字符串数组的公共前缀
public boolean isCommonPrefix(String[] strs, int length) {
// 获取第一个字符串的指定长度前缀
String str0 = strs[0].substring(0, length);
int count = strs.length;
// 遍历剩余的字符串,逐个比较前缀字符
for (int i = 1; i < count; i++) {
String str = strs[i];
for (int j = 0; j < length; j++) {
if (str0.charAt(j) != str.charAt(j)) {
return false;
}
}
}
// 返回是否是公共前缀的结果
return true;
}
}
说明:
longestCommonPrefix() 方法用于求取字符串数组 strs 中的最长公共前缀。
首先判断字符串数组是否为空或长度为0,如果是,则直接返回空字符串。 获取字符串数组中最短字符串的长度 minLength。
使用二分查找的思路来查找最长公共前缀。 维持一个区间 [low, high],初始为 [0, minLength]。
在每一次循环中,取区间的中间位置 mid。 判断以mid长度作为前缀是否是字符串数组的公共前缀,通过调用 isCommonPrefix()
方法实现。 如果是公共前缀,则更新 low = mid,继续查找右半部分。 如果不是公共前缀,则更新 high = mid -
1,继续查找左半部分。 当 low >= high 时,二分查找结束,得到最长公共前缀的长度。 返回最长公共前缀,使用
strs[0].substring(0, low) 来截取对应长度的前缀。 isCommonPrefix()
方法用于判断指定长度的前缀是否是字符串数组 strs 的公共前缀。 获取第一个字符串的指定长度前缀 str0。
遍历剩余的字符串,逐个比较前缀中的字符。 如果存在不相等的字符,说明不是公共前缀,返回 false。
如果所有字符串的前缀字符都相等,说明是公共前缀,返回 true。
C语言版本
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
// 函数声明
char* longestCommonPrefix(char** strs, int strsSize);
int isCommonPrefix(char** strs, int strsSize, int len);
/**
int main() {
// 测试数据
char* strs[] = {"flower", "flow", "flight"};
int strsSize = 3;
// 调用函数并打印结果
char* result = longestCommonPrefix(strs, strsSize);
printf("Longest Common Prefix: %s\n", result);
return 0;
}
**/
/*
* 获取字符串数组中的最长公共前缀
* 参数: strs - 字符串数组, strsSize - 字符串数组的长度
* 返回值: 最长公共前缀的指针
*/
char* longestCommonPrefix(char** strs, int strsSize) {
// 如果字符串数组为空或长度为0,直接返回空字符串
if (strs == NULL || strsSize == 0) {
return "";
}
// 找出最短字符串的长度
int minLength = INT_MAX;
for (int i = 0; i < strsSize; i++) {
int len = strlen(strs[i]);
if (len < minLength) {
minLength = len;
}
}
// 使用二分法查找最长公共前缀
int low = 1;
int high = minLength;
int mid = 0;
while (low <= high) {
mid = (low + high) / 2;
if (isCommonPrefix(strs, strsSize, mid)) {
low = mid + 1;
} else {
high = mid - 1;
}
}
// 根据最长公共前缀的长度,创建并返回结果字符串
char* result = (char*)malloc((mid + 1) * sizeof(char));
strncpy(result, strs[0], mid);
result[mid] = '\0';
return result;
}
/*
* 判断指定长度前缀是否是字符串数组的公共前缀
* 参数: strs - 字符串数组, strsSize - 字符串数组的长度, len - 前缀长度
* 返回值: 是否是公共前缀的整数值,1为是,0为否
*/
int isCommonPrefix(char** strs, int strsSize, int len) {
for (int i = 0; i < len; i++) {
char ch = strs[0][i];
for (int j = 1; j < strsSize; j++) {
if (strs[j][i] != ch) {
return 0;
}
}
}
return 1;
}
说明:
longestCommonPrefix()函数用于找到字符串数组中的最长公共前缀。
在函数中,首先判断字符串数组是否为空或长度为0。如果是,则直接返回空字符串。 找出字符串数组中最短字符串的长度minLength。
使用二分法来查找最长公共前缀。 初始化low为1,high为最短字符串的长度minLength。 循环遍历,直到找到最长公共前缀的长度。
设置mid为low和high的中间值。 如果前缀长度为mid的前缀是字符串数组的公共前缀,则在[mid+1, high]范围继续查找。
如果前缀长度为mid的前缀不是字符串数组的公共前缀,则在[low, mid-1]范围继续查找。
根据最长公共前缀的长度mid,动态分配内存创建结果字符串result。
使用strncpy()函数将字符串数组的第一个字符串的前mid个字符复制到结果字符串中。 在结果字符串的末尾添加结束符’\0’。
返回结果字符串的指针。 请注意,在使用完结果字符串后,不要忘记使用free()函数释放分配的内存。
Python3版本
def longestCommonPrefix(strs):
# 如果字符串数组为空或长度为0,直接返回空字符串
if not strs:
return ""
# 找出最短字符串的长度
minLength = min(len(s) for s in strs)
# 使用二分法查找最长公共前缀
low = 1
high = minLength
while low <= high:
mid = (low + high) // 2
if isCommonPrefix(strs, mid):
low = mid + 1
else:
high = mid - 1
# 根据最长公共前缀的长度,返回结果字符串
return strs[0][:low]
def isCommonPrefix(strs, length):
for i in range(length):
ch = strs[0][i]
for j in range(1, len(strs)):
if strs[j][i] != ch:
return False
return True
# 调用函数并打印结果
#strs = ["flower", "flow", "flight"]
#result = longestCommonPrefix(strs)
#print("Longest Common Prefix:", result)
说明:
longestCommonPrefix() 函数用于找到字符串数组中的最长公共前缀。
首先判断字符串数组是否为空。如果为空,则直接返回空字符串。 找出字符串数组中最短字符串的长度 minLength,使用 min()函数和生成器表达式来实现。 使用二分法来查找最长公共前缀。 初始化 low 为 1,high 为最短字符串的长度 minLength。
循环遍历,直到找到最长公共前缀的长度。 设置 mid 为 low 和 high 的中间值。 如果前缀长度为 mid
的前缀是字符串数组的公共前缀,则在 [mid+1, high] 范围继续查找。 如果前缀长度为 mid 的前缀不是字符串数组的公共前缀,则在[low, mid-1] 范围继续查找。 根据最长公共前缀的长度 low,返回结果字符串,使用切片操作实现。
isCommonPrefix() 函数用于判断指定长度的前缀是否是字符串数组的公共前缀。
使用嵌套循环遍历前缀的每个字符,逐个比较所有字符串的对应位置字符。 如果存在不相等的字符,说明不是公共前缀,返回 False。
如果所有字符串的前缀字符都相等,说明是公共前缀,返回 True。 调用函数并打印结果,使用示例字符串数组。
复杂度分析
- 时间复杂度:O(mnlogm),其中 m 是字符串数组中的字符串的最小长度,n 是字符串的数量。二分查找的迭代执行次数是 O(logm),每次迭代最多需要比较 mn 个字符,因此总时间复杂度是 O(mnlogm)。
- 空间复杂度:O(1)。使用的额外空间复杂度为常数。
克隆图(LeetCode 133,Medium)
- 标签:图的遍历、深拷贝
题目
在这里插入代码片
思路及实现
方式一:暴力解法(不推荐)
思路
代码实现
Java
在这里插入代码片
C
在这里插入代码片
Python
在这里插入代码片
复杂度分析
- 时间复杂度
- 空间复杂度
方式二:暴力解法(不推荐)
思路
代码实现
Java
在这里插入代码片
C
在这里插入代码片
Python
在这里插入代码片
复杂度分析
- 时间复杂度
- 空间复杂度
合并排序的数组(LeetCode 88,Easy)
- 标签:归并排序、数组操作
题目
在这里插入代码片
思路及实现
方式一:暴力解法(不推荐)
思路
代码实现
Java
在这里插入代码片
C
在这里插入代码片
Python
在这里插入代码片
复杂度分析
- 时间复杂度
- 空间复杂度
方式二:暴力解法(不推荐)
思路
代码实现
Java
在这里插入代码片
C
在这里插入代码片
Python
在这里插入代码片
复杂度分析
- 时间复杂度
- 空间复杂度
第 K 个数(LeetCode 215,Medium)
- 标签:快速选择、二分查找
题目
在这里插入代码片
思路及实现
方式一:暴力解法(不推荐)
思路
代码实现
Java
在这里插入代码片
C
在这里插入代码片
Python
在这里插入代码片
复杂度分析
- 时间复杂度
- 空间复杂度
方式二:暴力解法(不推荐)
思路
代码实现
Java
在这里插入代码片
C
在这里插入代码片
Python
在这里插入代码片
复杂度分析
- 时间复杂度
- 空间复杂度
结语
经典的数据结构与算法题目不仅考察我们的解题思路和编程能力,更重要的是让我们深入理解各种数据结构和算法的原理和应用。通过解题,我们可以不断提高自己的编程能力,锻炼思维的敏捷性。同时,也能够给我们带来一些乐趣和满足感。
希望这些有趣的题目能够给你带来启发和帮助,让你更加热爱并深入学习数据结构与算法。加油,继续挑战,我们一起做个优秀的开发者!


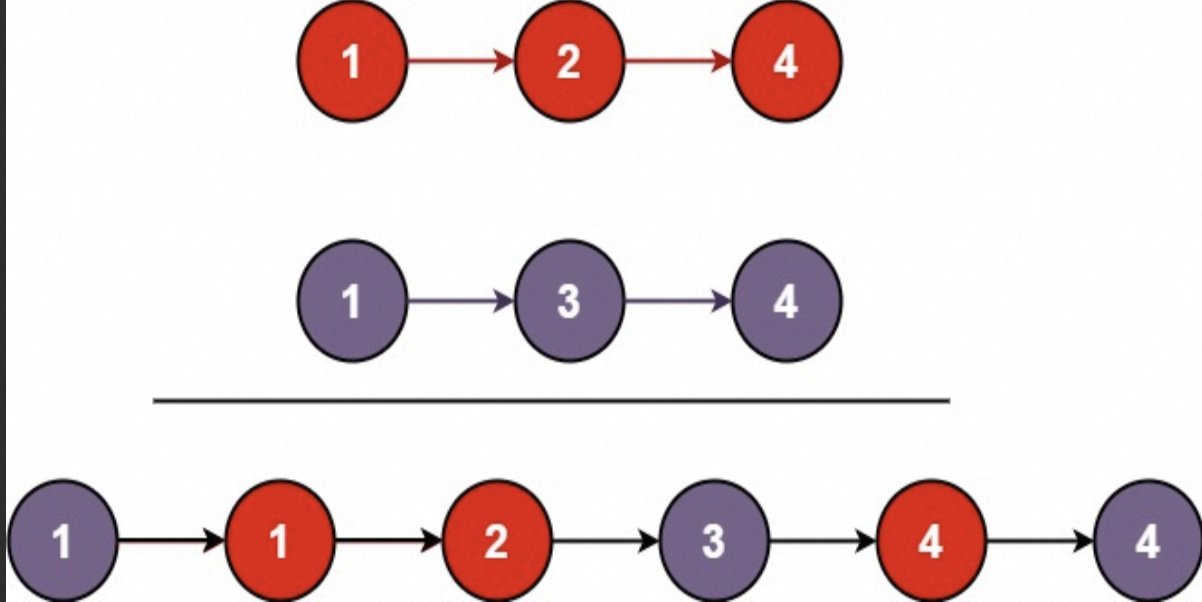 > 输入:l1 = [1,2,4], l2 = [1,3,4] 输出:[1,1,2,3,4,4]
> 输入:l1 = [1,2,4], l2 = [1,3,4] 输出:[1,1,2,3,4,4]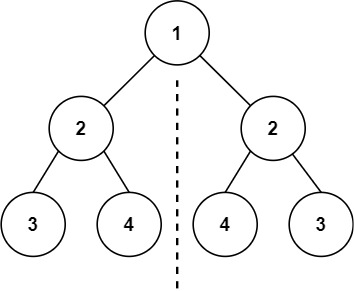


 浙公网安备 33010602011771号
浙公网安备 33010602011771号