机器学习:SVM(目标函数推导:Hard Margin SVM、Soft Margin SVM)
一、Hard Margin SVM
- SVM 的思想,最终用数学表达出来,就是在优化一个有条件的目标函数:
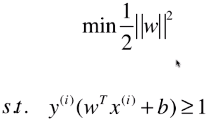
- 此为 Hard Margin SVM,一切的前提都是样本类型线性可分;
1)思想
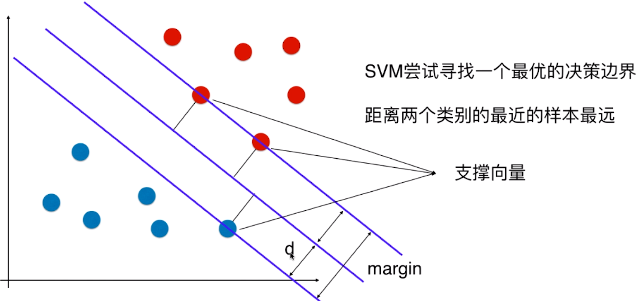
- SVM 算法的本质就是最大化 margin;
- margin = 2d,SVM 要最大化 margin,也就是要最大化 d,所以只要找到 d 的表达式,也能解决相应的问题;
2)特征空间中样本点到决策边界的距离
-
二维平面中:

-
n 维空间中:
- 此处 n 维空间并不是 3 维的立体空间,而是指 n 个方面,或 n 个特征,表示要从 n 个方面理解和分析样本;
- 此处所说的 n 维空间中的点到直线的距离,只是相对于 二维 特征平面的说法,
- 直线的表达式:
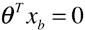 ,或者:
,或者: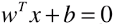 ;
; - 如果样本 x 中有 n 种特征,θ 和 xb 中都有 (n + 1) 个元素;w 向量中有 n 个元素;
- b 和 θ0 是截距;
- 点到直线的距离:
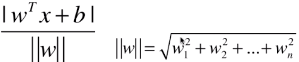 ;
;
3)样本在特征空间中药满足的条件
- 训练数据集中,所有的样本点到决策边界的距离都大于或等于 d;
- 此处样本的两种类型:1、-1;(不在称为 0 、1,是为了方便计算;其实称为什么都无所谓,只要能很好的区分开不同的类别)
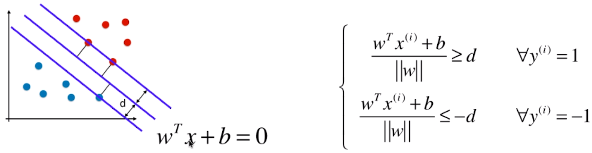
- i:表示第 i 个样本,其类型 y(i) 分两种情况:1、-1;
- ≤ -d:因为 -1 类型的样本点,带入模型时,decision_function() 方法求的结果都小于 0,此处将绝对值符号去掉后的状态;
- = d 时:表示支撑向量到决策边界的距离;
-
第一次变形:
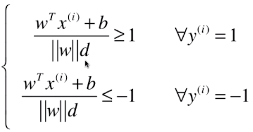
-
第二次变形:
- 由于 ||w||d 和 b 都是常量,公式进一步变形:分子、分母同时除以 ||w||d;
-
第三次变形:
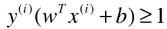
- 其中 y(i) 有1、-1 两种分类结果,也就是训练数据集的所有样本都要满足这个关系式;
- 如果 wT.x(i) + b ≥ 1,也就是
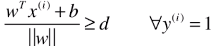 ,则:
,则: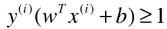
- 如果 wT.x(i) + b ≤ -1,也就是
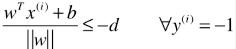 ,则:
,则: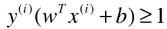
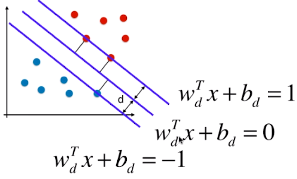
4)决策边界及由支撑向量觉得的直线的方程
-
3 条直线的方程(一):
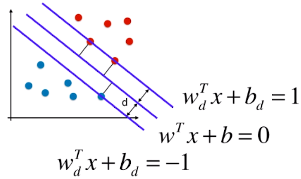
-
3 条直线方程(二):
- 由于 ||w||d 和 b 都是常量,直线方程进一步变形:分子、分母同时除以 ||w||d;
-
3 条直线方程(三)
- 更改 wd 和 bd 的名称:w、b;
- 此处的 w 向量 和 b 常量,
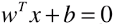 中的 w 向量和 b 常量不同,他们之间相差了一个系数 ||w||d;
中的 w 向量和 b 常量不同,他们之间相差了一个系数 ||w||d;
-
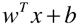 = 1 / -1 时,表示支撑向量到决策边界的距离;
= 1 / -1 时,表示支撑向量到决策边界的距离;
5)目标函数
-
d 表示支撑向量到决策边界的距离,则有 | wT.x + b | = 1,d = | wT.x + b | / ||w|| = 1 / ||w|| ,为了使 d 最大,就要使 ||w|| 尽可能的小;
- 目标函数:||w||,求目标函数最小值;
- 目标函数变形:
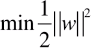 ;
;
- 变形原因:为了方便求导而改变目标函数;
- 前提条件:
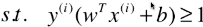 ,也就是优化该目标函数的时是有前提条件的;
,也就是优化该目标函数的时是有前提条件的;
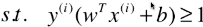 是由 ( | wT.x(i) + b | / ||w|| ) ≥ d 推导出来的;
是由 ( | wT.x(i) + b | / ||w|| ) ≥ d 推导出来的;- s.t.(such that):用在限定条件之前,表示该表达式为限定条件;
-
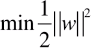 和
和 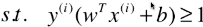 中的 w 向量并不是模型
中的 w 向量并不是模型 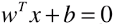 中的 w 向量,两者之间相差一个系数:||w||d,且系数中的 ||w|| 指模型
中的 w 向量,两者之间相差一个系数:||w||d,且系数中的 ||w|| 指模型 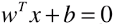 中的 w 向量;
中的 w 向量;
6)其它
- 没有前提条件的最优化,称为全局最优化;
- 全局最优化问题:直接对目标函数求导,让导数等于 0,相应的极值点就有可能是所要求的最大值或者最小值;
- 有条件的最优化问题,在最优化领域,解决该问题的方法与没有条件的最优化问题差异很大;
- 有条件的最优化问题:较复杂,需要使用拉布拉斯算子进行求解;
二、Soft Margin SVM
1)目标函数
- C 为超参数
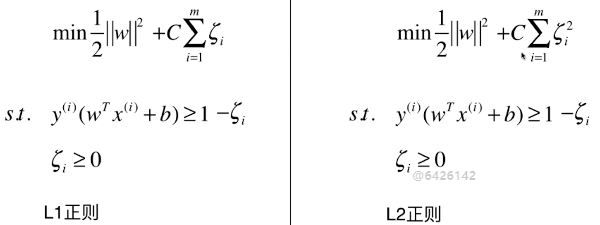
- C = 1:两者比重相同;
- C > 1:主要优化后半部分;
- C < 1:住哟啊优化前半部分;
- C 越大,容错空间越小;C 越小,容错空间越大;
2)Hard Margin SVM 算法面临的问题
- Hard Margin SVM:本质上就是求解如图的有条件的最优化问题,求出向量 w ,也就是求出模型的支撑向量机;
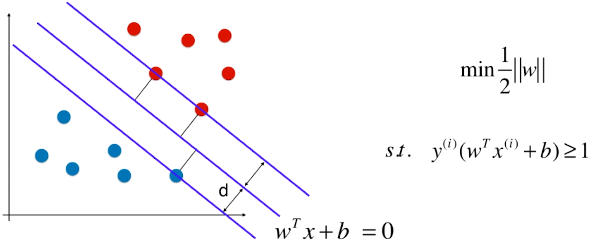
- 现象:有些样本比价特殊或者样本错误(如图1)、有些样本的分布不是线性可分的(如图2);
 、
、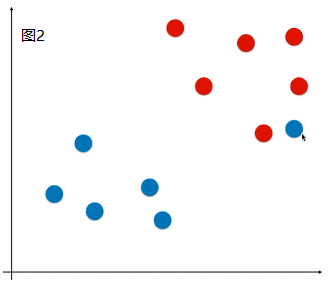
- 问题:针对这两种现象,使用 Hard Margin SVM,如图,得到的决策边界不准确;(如果是图 2 的情况,使用 Hard Margin SVM 根本得不到模型)
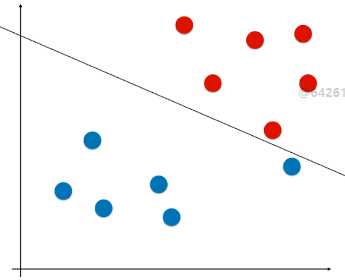
3)Soft Margin SVM 的思路
- 思路:人为的去除掉这些特殊的或者错误的样本点;
- Soft Margin SVM 要具有容一定的错能力;
- 这里的错,指数据或样本本身的异常或错误,而不是算法本身的错误;
- 思考一个机制:对于这个机制,SVM 算法得到的决策边界要有一定的容错能力,在一些情况下,该机制应该考虑,在一定情况下可以将一些样本进行错误分类,最终使得模型的泛化能力尽可能的高;
- 模型的目的或要求:实践应用中的泛化能力高,具体怎么得到这个模型则无关紧要;
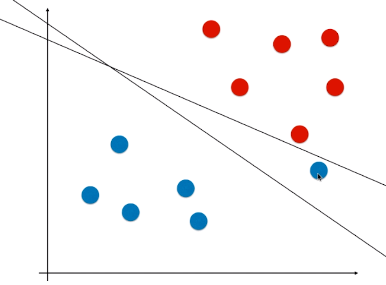
4)Soft Margin SVM 的损失函数推导
-
Hard Margin SVM 中:
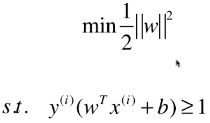
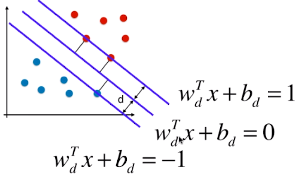
- 前提条件:所有的样本点都必须在 = 1/-1 这两天直线的外侧;
- Soft Margin SVM 去除异常样本的方法:扩大该限定条件,设定容错空间,允许个别极端的或者错误的样本点,分布在支撑向量所在直线与决策边界之间的区域;
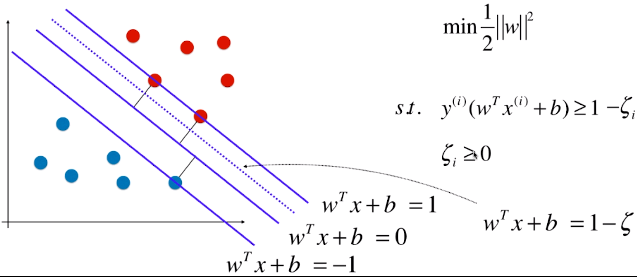
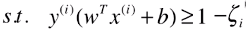 :模型允许模型犯一定的错误,允许一些样本分布在虚线与 =1 的直线之间;
:模型允许模型犯一定的错误,允许一些样本分布在虚线与 =1 的直线之间;- ζ 不是 一个固定的值,对任意一个样本 x(i) 都有一个 ζi 与其对应;如果有 m 个样本点,则有 m 个 ζ 值,每一个样本都有其容错空间;
- ζ 要做的是,希望模型有一定的容错空间,但范围不能太大;
-
怎么表示容错空间不能太大?
- 方案:更改目标函数,两部分之间取得平衡;
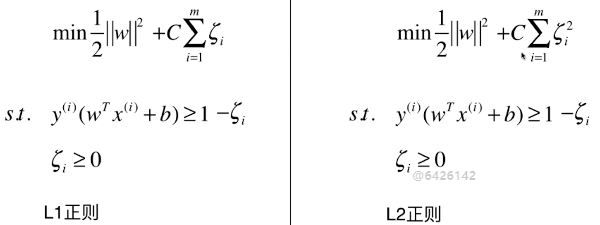
5)其它
- Hard Margin SVM 和 Soft Margin SVM 都是线性 SVM (也就是 Linear SVM),只是有些问题中的样本分布线性可分,有些问题中的样本不能完全线性可分(存在极端样本、或者错误的样本);
- 得到的决策边界都是一条直线,在高维空间中是一个平面;
- 正则化的目的:使模型针对训练数据集有更高的容错能力,使得模型对训练数据集中的极端样本点不那么敏感,进而提升模型的泛化能力;
- 思想:所谓的正则化,本质是一个概念,并不是对于所有的模型添加了正则项都是同样的 L1 范式、L2 范式;对于有些模型,需要改变正则化的策略;但是正则化所要实现的效果是一样的——提升模型的泛化能力。


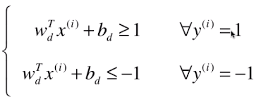
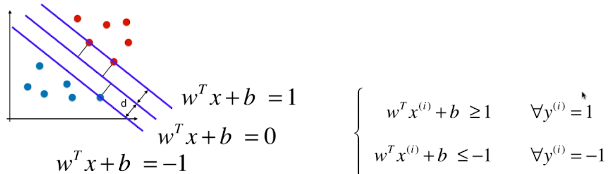


· 10年+ .NET Coder 心语,封装的思维:从隐藏、稳定开始理解其本质意义
· .NET Core 中如何实现缓存的预热?
· 从 HTTP 原因短语缺失研究 HTTP/2 和 HTTP/3 的设计差异
· AI与.NET技术实操系列:向量存储与相似性搜索在 .NET 中的实现
· 基于Microsoft.Extensions.AI核心库实现RAG应用
· 阿里巴巴 QwQ-32B真的超越了 DeepSeek R-1吗?
· 10年+ .NET Coder 心语 ── 封装的思维:从隐藏、稳定开始理解其本质意义
· 【译】Visual Studio 中新的强大生产力特性
· 【设计模式】告别冗长if-else语句:使用策略模式优化代码结构
· 字符编码:从基础到乱码解决