机器学习：逻辑回归（决策边界）

一、基础理解

• 决策边界：在特征空间内，根据不同特征对样本进行分类，不同类型间的分界就是模型针对该数据集的决策边界。

• 决策边界，用于分类问题中，通过决策边界可以更好的可视化分类结果；

• 在二维特征空间中，决策边界为一条直线，理论上，在该直线上 θ.T.x = 0，但实际上不一定存在这样的样本点；

• 通过决策边界可以直接根据样本在特征空间的位置对该样本的类型进行预测；

• 满足决策边界条件的样本点，分为哪一类都可以，但实际应用中很少发生；

• 作用：得到一个模型后，可以直接绘制该模型的决策边界，然后再绘制出需要预测的样本点，根据样本点相对于特征空间中的决策边界的分布，直接预测样本的类型；

1. 通过决策边界可以直接根据样本在特征空间的位置对该样本的类型进行预测；

• 决策：根据样本发生概率 p 的值，到底将该样本分为哪一类？
• 边界：
• 1）函数 σ(t) 的特点，t > 0 时σ(t) > 0.5（也就是 P > 0.5）；t < 0 时σ(t) < 0.5（也就是 P < 0.5）；　
•   　 　
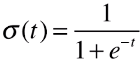
• 2）也就是 ý 的最终预测结果，由 θ^T.x_b 决定，决定的边界条件就是 θ^T.x_b = 0；
• 

 

 

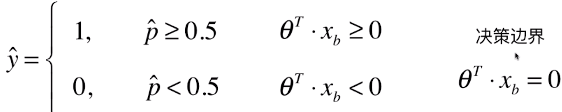
二、两种特征的数据集的决策边界（限线性回归、逻辑回归）

• 二维特征空间中，决策边界是一条理论上的直线，该直线是有线性模型的系数和截距决定的，并不一定有样本满足此条件；

• 如果样本只有两个特征，决策边界可以表示为：
• θ^T.x_b = θ₀ + θ₁.x₁ + θ₂.x₂ = 0，则该边界是一条直线，因为分类问题中特征空间的坐标轴都表示特征；

1. 则有：；

 

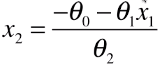　1）在二维特征空间中绘制决策边界

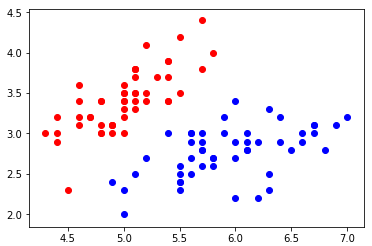
• 模拟数据集并绘制

  import numpy as np
  import matplotlib.pyplot as plt
  from sklearn import datasets
  
  iris = datasets.load_iris()
  
  X = iris.data
  y = iris.target
  X = X[y<2, :2]
  y = y[y<2]
  
  plt.scatter(X[y==0, 0], X[y==0, 1], color='red')
  plt.scatter(X[y==1, 0], X[y==1, 1], color='blue')
  plt.show()

  

   

• 用自己的逻辑回归算法训练模型并绘制模型针对模拟数据集的决策边界

  from playML.train_test_split import train_test_split
  
  X_train, X_test, y_train, y_test = train_test_split(X, y, seed=666)
  
  
  from playML.LogisticRegression import LogisticRegression
  
  log_reg = LogisticRegression()
  log_reg.fit(X_train, y_train)
  
  # x2()函数：求满足决策边界关系的直线的函数值；
  def x2(x1):
      return (-log_reg.coef_[0] * x1 - log_reg.intercept_) / log_reg.coef_[1]
  
  x1_plot = np.linspace(4, 8, 1000)
  x2_plot = x2(x1_plot)
  
  plt.scatter(X[y==0, 0], X[y==0, 1], color='red')
  plt.scatter(X[y==1, 0], X[y==1, 1], color='blue')
  plt.plot(x1_plot, x2_plot)
  plt.show()

  

 

 

三、不规则的决策边界的绘制方法

• 思路：特征空间中分布着无数的点，通过细分，将特征空间分割无数的点，对于每一个点都使用模型对其进行预测分类，将这些预测结果绘制出来，不同颜色的点的边界就是分类的决策边界；

• 分割方法：将特征空间的坐标轴等分为 n 份（可视化时只显示两种特征），则特征空间被分割为 n X n 个点（每个点相当于一个样本），用模型预测这 n² 个点的类型，经预测结果（样本点）显示在特征空间；

 

　1） 将绘制决策边界的代码封装起来

• # plot_decision_boundary()函数：绘制模型在二维特征空间的决策边界；
  def plot_decision_boundary(model, axis):
      # model：算法模型；
      # axis：区域坐标轴的范围，其中 0,1,2,3 分别对应 x 轴和 y 轴的范围；
      
      # 1）将坐标轴等分为无数的小点，将 x、y 轴分别等分 （坐标轴范围最大值 - 坐标轴范围最小值）*100 份，
      # np.meshgrid()：
      x0, x1 = np.meshgrid(
          np.linspace(axis[0], axis[1], int((axis[1]-axis[0])*100)).reshape(-1,1),
          np.linspace(axis[2], axis[3], int((axis[3]-axis[2])*100)).reshape(-1,1)
      )
      # np.c_()：
      X_new = np.c_[x0.ravel(), x1.ravel()]
      
      # 2）model.predict(X_new)：将分割出的所有的点，都使用模型预测
      y_predict = model.predict(X_new)
      zz = y_predict.reshape(x0.shape)
      
      # 3）绘制预测结果
      from matplotlib.colors import ListedColormap
      custom_cmap = ListedColormap(['#EF9A9A','#FFF59D','#90CAF9'])
      
      plt.contourf(x0, x1, zz, linewidth=5, cmap=custom_cmap)

   

 

四、绘制不同模型的决策边界（使用模拟的数据集训练模型）

　1）绘制逻辑回归算法的模型的决策边界

• plot_decision_boundary(log_reg, axis=[4, 7.5, 1.5, 4.5])
  plt.scatter(X[y==0, 0], X[y==0, 1], color='red')
  plt.scatter(X[y==1, 0], X[y==1, 1], color='blue')
  plt.show()

  

1. 两种色块就是将特征空间分割成 n² 个样本点的分类结果；两种色块的分界线就是该模型的决策边界；

 

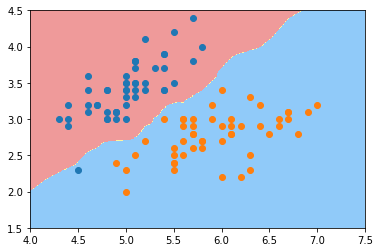
　2）绘制 kNN 算法的模型的决策边界（ 2 种样本）

• from sklearn.neighbors import KNeighborsClassifier
  
  knn_clf = KNeighborsClassifier()
  knn_clf.fit(X_train, y_train)
  
  plot_decision_boundary(knn_clf, axis=[4, 7.5, 1.5, 4.5])
  plt.scatter(X[y==0, 0], X[y==0, 1])
  plt.scatter(X[y==1, 0], X[y==1, 1])
  plt.show()

  

 

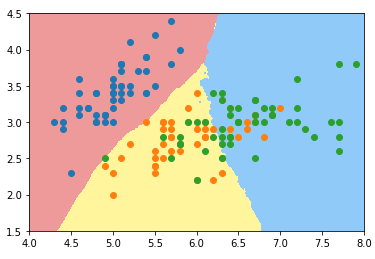
　3）绘制 kNN 算法的模型的决策边界（ 3 种样本）

• 代码

  knn_clf_all = KNeighborsClassifier()
  knn_clf_all.fit(iris.data[:,:2], iris.target)
  # 输出：KNeighborsClassifier(algorithm='auto', leaf_size=30, metric='minkowski',
             metric_params=None, n_jobs=1, n_neighbors=5, p=2,
             weights='uniform')
  
  plot_decision_boundary(knn_clf_all, axis=[4, 8, 1.5, 4.5])
  plt.scatter(iris.data[iris.target==0,0], iris.data[iris.target==0,1])
  plt.scatter(iris.data[iris.target==1,0], iris.data[iris.target==1,1])
  plt.scatter(iris.data[iris.target==2,0], iris.data[iris.target==2,1])
  plt.show()

  

• 问题

1. 决策边界不规则，图中黄色区域和蓝色区域的界限不明显；
2. 黄色区域存在绿色的点，蓝色区域存在橙色的点；

• 原因：模型可能过拟合；
• 方案：重新调整参数训练模型；

1. n_neighbors=5，模型的 k 参数选择了 5，太小，导致模型太复杂；（kNN 算法中，k 值越小模型越复杂）

 

• 更改 k 参数，重新绘制

  knn_clf_all = KNeighborsClassifier(n_neighbors=50)
  knn_clf_all.fit(iris.data[:,:2], iris.target)
  # 输出：KNeighborsClassifier(algorithm='auto', leaf_size=30, metric='minkowski',
             metric_params=None, n_jobs=1, n_neighbors=50, p=2,
             weights='uniform')
  
  plot_decision_boundary(knn_clf_all, axis=[4, 8, 1.5, 4.5])
  plt.scatter(iris.data[iris.target==0,0], iris.data[iris.target==0,1])
  plt.scatter(iris.data[iris.target==1,0], iris.data[iris.target==1,1])
  plt.scatter(iris.data[iris.target==2,0], iris.data[iris.target==2,1])
  plt.show()