机器学习：PCA（降噪）
一、噪音
- 噪音产生的因素：可能是测量仪器的误差、也可能是人为误差、或者测试方法有问题等；
- 降噪作用：方便数据的可视化，使用样本特征更清晰；便于算法操作数据；
- 具体操作：从 n 维降到 k 维，再讲降维后的数据集升到 n 维，得到的新的数据集为去燥后的数据集；
- 降维：X_reduction = pca.transform ( X )
- 升维：X_restore = pca.inverse_transform ( X_reduction )，数据集 X_restore 为去燥后的数据集；
二、实例
1）例一
-
模拟并绘制样本信息
import numpy as np import matplotlib.pyplot as plt X = np.empty((100, 2)) X[:, 0] = np.random.uniform(0., 100, size=100) X[:, 1] = 0.75 * X[:, 0] + 3. + np.random.normal(0, 5, size=100) plt.scatter(X[:, 0], X[:, 1]) plt.show()
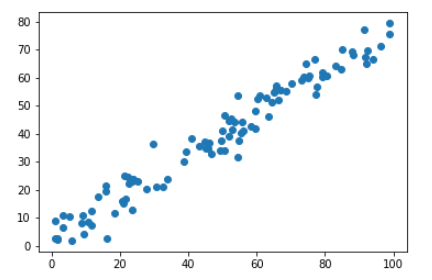
- 实际上，样本的状态看似在直线上下抖动式的分布，其实抖动的距离就是噪音；
-
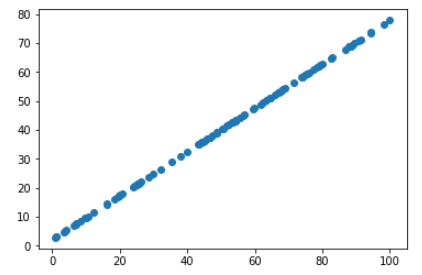
使用 PCA 降维，达到降噪的效果
- 操作：数据降维后，再升到原来维度；
- inverse_transform(低维数据)：将低维数据升为高维数据
-
from sklearn.decomposition import PCA pca = PCA(n_components=1) pca.fit(X) X_reduction = pca.transform(X) # inverse_transform(低维数据)：将低维数据升为高维数据 X_restore = pca.inverse_transform(X_reduction) plt.scatter(X_restore[:,0], X_restore[:,1]) plt.show()
2）例二（手写识别数字数据集）
-
加载数据集（人为加载噪音：noisy_digits）
from sklearn import datasets digits = datasets.load_digits() X = digits.data y = digits.target # 在数据集 X 的基础上创建一个带噪音的数据集 noisy_digits = X + np.random.normal(0, 4, size=X.shape)
-
从带有噪音的数据集 noisy_digits 中提出示例数据集 example_digits
example_digits = noisy_digits[y==0,:][:10] for num in range(1, 10): X_num = noisy_digits[y==num,:][:10] # np.vstack([array1, array2])：将两个矩阵在水平方向相加，增加列数； # np.hstack([array1, array2])：将两矩阵垂直相加，增加行数； example_digits = np.vstack([example_digits, X_num]) example_digits.shape # 输出：（100, 64）
-
绘制示例数据集 example_digits（带噪音）
def plot_digits(data): fig, axes = plt.subplots(10, 10, figsize=(10,10), subplot_kw = {'xticks':[], 'yticks':[]}, gridspec_kw=dict(hspace=0.1, wspace=0.1)) for i, ax in enumerate(axes.flat): ax.imshow(data[i].reshape(8, 8), cmap='binary', interpoltion='nearest', clim=(0, 16)) plt.show() plot_digits(example_digits)
-
降噪数据集 example_digits
# 如果噪音比较多，保留较少信息（此例中只保留 50% 的信息） pca = PCA(0.5) pca.fit(noisy_digits) # 查看最终的样本维度 pca.n_components_ # 输出：12 # 1）降维：将数据集 example_digits 降维，得到数据集 components components = pca.transform(example_digits) # 2）升维：将数据集升到原来维度（100, 64） filtered_digits = pca.inverse_transform(components) # 绘制去燥后的数据集 filtered_digits plot_digits(filtered_digits)
