机器学习：批量梯度下降法（线性回归中的使用）

一、推导目标函数

　1）基础概念

多元线性回归模型：
多元线性回归的损失函数：
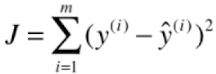
参数 theta：θ = (θ₀, θ₁, θ_{3, ...,}θ_n)
n：表示模型中有 n 个特征参数；
θ₁：表示
梯度：，对每一个 θ_i 求一次偏导数；
梯度代表方向：对应 J 增大最快的方向；
偏导数：函数 J 中含有 n 个未知数，每次知道其中的一个未知数求导，其它数看作常量，求得的数是函数 J 的偏导数；
学习率：η
theta每次变化量： | 学习率 X 梯度 | == -η * ▽J ；（带负号 “ - ” ，因为损失函数与参数负相关，其导数值为负，变化量要为正数）

　2）梯度下降原理

此图为有两个参数的梯度下降法的可视化：z = x² + 2y²；
一圈圈的红线为等高线，也就是每次参数x、y的变化后目标函数 z 的取值；
越外圈的 z 的取值越大，中心位置表示 z 的最小值；
z 的取值可以延不同的方向逐层下降，箭头表示梯度下降的方向，也是 z 的取值变化最快的方向；
圈与圈之间的间距为目标函数 z 的变化量；
最外圈的间距较大，也就是 z 的变化量较大；

　3）推导目标函数

线性回归算法中的目标函数的第一次变形

分析目标函数

▽J(θ) 中，θ 是未知数，X 是样本中的已知数；
公式变形思路：▽J(θ) 中的每一项都是 m 项的求和，因此梯度的大小跟样本数量有关，样本数量越大，梯度中的每一个元素值也就越大，因此所求得的梯度中的每一个元素的值，受到了 m 的影响，而在优化的过程中，梯度中的每一个元素的值最好和 m 无关；

确定最终的目标函数

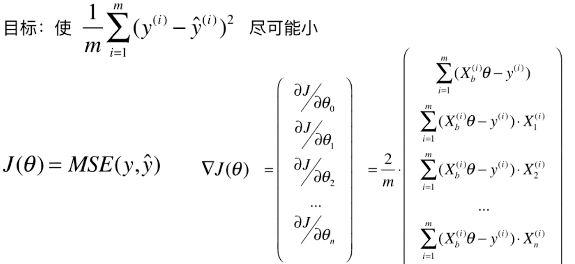
目标函数变形——确定使用梯度法所要优化的最终的目标函数：J(θ) = MSE (y, ý)
添加一个 1/m 是为了减小梯度的元素值；

　4）思考总结

当使用梯度下降法求解目标函数的最小值时，需要特殊设计目标函数，不见得所有的目标函数都非常合适此方法，虽然理论上即使梯度中的元素值很大，依然可以通过调整 η 得到想要的结果，但是这样可能会影响效率；

二、算法的实现（1）

　1）解决简单线性回归算法

模拟简单线性回归

import numpy as np

np.random.seed(666)
x = 2 * np.random.random(size=100)
y = x * 3. + 4. + np.random.normal(size=100)

X = x.reshape(-1, 1)

# np.random.normal(size=100)：噪音，用均值为0，方差为1的随机正态分布生成

计算损失函数值（损失函数：J(θ) = MSE(y, ý)）

# x_b：变形后的X_train中的Xb，增加了第一列全为1之后的矩阵
# y：y_train
def J(theta, x_b, y):
    try:
        return np.sum((y - x_b.dot(theta)) ** 2) / len(x_b)
    except:
        return float('inf')

# 计算损失函数的过程中要进行一场捕捉：正常运行时执行try，出现异常时执行except；

计算梯度值（梯度：▽J(θ)）

def gradient_descent(x_b, y, initial_theta, eta, n_iters = 10**4, epsilon=10**-8):
    
    theta = initial_theta
    i_iter = 0
    
    while i_iter < n_iters:
        gradient = dJ(theta, x_b, y)
        last_theta = theta
        theta = theta - eta * gradient
    
        if(abs(J(theta, x_b, y) - J(last_theta, x_b, y)) < epsilon):
            break
         
        i_iter += 1
        
    return theta

x_b：变形后的X_train数据集；
y：训练数据集y_train；
initial_theta：用于存储搜索过程中的theta值；
eta：xuexilv；
n_iters：搜索循环的次数；
epsilon：搜索精度；

初始化theta和eta

# 变形数据集X，得到x_b
x_b = np.hstack([np.ones((len(X), 1), dtype=float), X])

# 初始化theta向量：使用便利 initial_theta，大小为x_b.shape[1]，也就是数据集的特征种类数
initial_theta = np.zeros(x_b.shape[1])

# 初始化eta
eta = 0.01

theta = gradient_descent(x_b, y, initial_theta, eta)
theta
# 输出：array([4.02145786, 3.00706277])

# theta[0]为截距，theta[1:]表示系数，这里也可以理解为斜率（简单线性回归中）；

　2）封装即调用

封装在线性回归算法LinearRegression类中，作为一种拟合方法

    def fit_gd(self, X_train, y_train, eta=0.01, n_iters=1e4):
        """根据训练数据集X_train, y_train, 使用梯度下降法训练Linear Regression模型"""
        assert X_train.shape[0] == y_train.shape[0], \
            "the size of X_train must be equal to the size of y_train"

        def J(theta, X_b, y):
            try:
                return np.sum((y - X_b.dot(theta)) ** 2) / len(y)
            except:
                return float('inf')

        def dJ(theta, X_b, y):
            res = np.empty(len(theta))
            res[0] = np.sum(X_b.dot(theta) - y)
            for i in range(1, len(theta)):
                res[i] = (X_b.dot(theta) - y).dot(X_b[:, i])
            return res * 2 / len(X_b)
            # return X_b.T.dot(X_b.dot(theta) - y) * 2. / len(X_b)

        def gradient_descent(X_b, y, initial_theta, eta, n_iters=1e4, epsilon=1e-8):

            theta = initial_theta
            cur_iter = 0

            while cur_iter < n_iters:
                gradient = dJ(theta, X_b, y)
                last_theta = theta
                theta = theta - eta * gradient
                if (abs(J(theta, X_b, y) - J(last_theta, X_b, y)) < epsilon):
                    break

                cur_iter += 1

            return theta

        X_b = np.hstack([np.ones((len(X_train), 1)), X_train])
        initial_theta = np.zeros(X_b.shape[1])
        self._theta = gradient_descent(X_b, y_train, initial_theta, eta, n_iters)

        self.intercept_ = self._theta[0]
        self.coef_ = self._theta[1:]

        return self

# self._theta：为LinearRegression类的参数；

　3）在Jupyter NoteBook中调用封装的代码

from LR.LinearRegression import LinearRegression

lin_reg = LinearRegression()
lin_reg.fit_gd(X, y)

# 查看系数
lin_reg.coef_
# 输出：array([3.00706277])

# 查看截距
lin_reg.intercept_
# 输出：4.021457858204859

三、梯度下降法的向量化和数据的标准化

　1）对梯度多向量化处理

对计算公式向量化后，使计算更简单
向量化过程

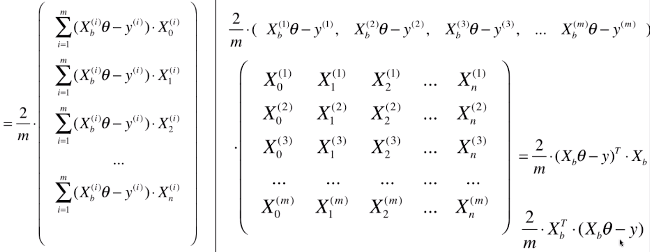
最终的向量化结果

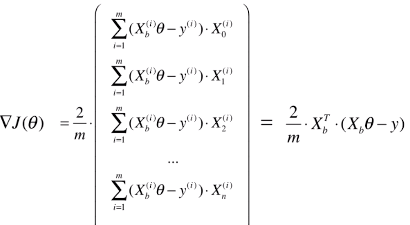
X_b^T == X_b . T：是 X_b 的转置矩阵;

改变梯度的计算方式（更改函数数 dJ():）

# res = np.empty(len(theta))
# res[0] = np.sum(X_b.dot(theta) - y)
# for i in range(1, len(theta)):
     # res[i] = (X_b.dot(theta) - y).dot(X_b[:, i])
# return res * 2 / len(X_b)

# 更换为：
return X_b.T.dot(X_b.dot(theta) - y) * 2. / len(X_b)

　2）实例

数据处理：分割

import numpy as np
from sklearn import datasets

boston = datasets.load_boston()
X = boston.data
y = boston.target

X = X[y < 50.0]
y = y[y < 50.0]

from ALG.data_split import train_test_split

X_train, X_test, y_train, y_test = train_test_split(X, y, seed=666)

使用正规方程优化损失函数

from LR.LinearRegression import LinearRegression

lin_reg1 = LinearRegression()

# %time 语句：返回该行代码执行所用的时间
%time lin_reg1.fit_normal(X_train, y_train)
lin_reg1.score(X_test, y_test)

# 输出：Wall time: 35.7 ms
       0.8129802602658466

使用梯度下降法优化损失函数

lin_reg2 = LinearRegression()
%time lin_reg2.fit_gd(X_train, y_train)
lin_reg2.score(X_test, y_test)

# 输出：Wall time: 478 ms
        nan

问题一：没有得到准确度，说明优化时损失函数没有收敛
分析：数据集中的数据值的大小差异较大，使用默认的 eta 求得的梯度非常大，使得梯度下降法的结果不收敛；
方案：修改 eata 值

修改 eta 值，再次优化

lin_reg2.fit_gd(X_train, y_train, eta=0.000001)

lin_reg2.score(X_test, y_test)
# 输出：0.2755663485338923

问题二：准确度太小（与正规方程优化结果比较而言）；
分析： eta 值太小，根据设定的循环次数没能找到损失函数的最小值；
方案：修改循环次数

修改循环次数（n_iters），再次优化

lin_reg2.fit_gd(X_train, y_train, eta=0.000001, n_iters=10**6)

lin_reg2.score(X_test, y_test)
# 输出：0.7541852353980764

问题三：准确度还是太小（与正规方程优化结果比较而言），没有到达损失函数的最小值；
分析：循环次数太小，或者 eta 值太小；
问题四：如果循环次数过大，或者 eta 太小，循环耗时比较大
分析（1）：之所以出现这种现象，因为整体的数据集的数值不在同一个规模上，也就是大小相差太大；
分析（2）：由于有 eta 这个变量，如果最终数据集的数据不在一个维度上（大小相差很大）将会影响梯度的结果，梯度的结果乘与 eta 是损失函数真正每次变化的步长，则步长有可能或者太大或者太小，如果步长太大会导致损结果不收敛，如果步长太小会导致搜索过程太慢；
方案：对数据集做归一化处理

用正规方程解线性回归的损失函数时，不需要对数据集归一化处理，因为正规方程中的模型的求解过程，整体变成了一个公式的计算，在公式计算过程中牵涉到的搜索的过程比较少

对数据做归一化处理，再次使用梯度下降法

from sklearn.preprocessing import StandardScaler

standardScaler = StandardScaler()
standardScaler.fit(X_train, y_train)


# 归一化处理数据
# X_train_standard：归一化后的训练数据集
# X_test_standard：归一化后的测试数据集
X_train_standard = standardScaler.transform(X_train)
X_test_standard = standardScaler.transform(X_test)


# 再次使用梯度下降法
lin_reg3 = LinearRegression()
%time lin_reg3.fit_gd(X_train_standard, y_train)
# 输出：Wall time: 233 ms
# 优点：没有更改默认的 eta 和循环次数 n_iters，fit 速度很快：269ms

lin_reg3.score(X_test_standard, y_test)
# 输出：0.8129880620122235
# 与正规化方程所得结果相近

　3）梯度下降法比正规化方程优化法的优势

实例

import numpy as np
from LR.LinearRegression import LinearRegression

m = 1000
n = 5000

big_x = np.random.normal(size=(m, n))
true_theta = np.random.uniform(0.0, 100.0, size=n+1)
big_y = big_x.dot(true_theta[1:]) + true_theta[0] + np.random.normal(0., 10, size=m)


# 正规方程法优化
big_reg1 = LinearRegression()
%time big_reg1.fit_normal(big_x, big_y)
# 输出：Wall time: 8.94 s


# 梯度下降法优化
big_reg2 = LinearRegression()
% time big_reg2.fit_gd(big_x, big_y)
# 输出：Wall time: 4.62 s

优点：使用梯度下降法优化，耗时更少
原因：正规方程处理的是 m 行 n 列的矩阵，对矩阵进行非常多的乘法运算，如果矩阵比较大时，用正规方程法优化耗时较多

问题：本次举例中，样本数量（m）小于特征量（n），目前在使用梯度下降法计算梯度时，要让每一个样本都参与计算，如果样本量比较大时，计算梯度也比较慢；
方案：使用随机梯度下降法

posted @ 2018-05-31 15:13 何永灿阅读(1560) 评论(0) 编辑收藏举报

刷新页面返回顶部

机器学习：批量梯度下降法（线性回归中的使用）

一、推导目标函数

1）基础概念

2）梯度下降原理

3）推导目标函数

4）思考总结

二、算法的实现（1）

1）解决简单线性回归算法

2）封装即调用

三、梯度下降法的向量化和数据的标准化

1）对梯度多向量化处理

2）实例

3）梯度下降法比正规化方程优化法的优势

公告

　1）基础概念

　2）梯度下降原理

　3）推导目标函数

　4）思考总结

　1）解决简单线性回归算法

　2）封装即调用

　1）对梯度多向量化处理

　2）实例

　3）梯度下降法比正规化方程优化法的优势