机器学习:调整kNN的超参数
一、评测标准
- 模型的测评标准:分类的准确度(accuracy);
- 预测准确度 = 预测成功的样本个数/预测数据集样本总数;
二、超参数
- 超参数:运行机器学习算法前需要指定的参数;
- kNN算法中的超参数:k、weights、P;
- 一般超参数之间也相互影响;
- 调参,就是调超参数;
1)问题
# 以kNN算法为例
- 平票:如果k个点中,不同类型的样本数相等,怎么选取?
- 如果选取的k个点中,数量多的一类样本点距离测试样本较远,数量少的一类样本点距离测试样本较近,此时选取数量较多的类型作为输出结果,不具说服力;
2)kNN算法中,除了K值外的另一个超参数:距离的权重(1/距离)
- k个点中,将不同类的点的权重相加,最大的那一类为目标标签
- scikit-learn库中的KNeighborsClassifier类中,还有一个weights()函数;
- 在__init__()中默认两个参数值:__init__(n_neighbors = 5, weights = 'uniform');
- weights = 'uniform',表示不考虑距离权重这个超参数;
- weights= 'distance',表示考虑距离权重这个超参数;
3)kNN算法的第三个超参数:P,距离参数
- P是有“明科夫斯基距离”得来的(详见“四、距离推导”),
- 只有当kNN算法考虑距离权重超参数(weights)时,才会考虑是否输入距离参数(P);
4)调参的方法
- 调参目的,找到最优的超参数;
- 机器学习算法应用在不同的领域中,不同领域内有其特有的知识
1、通过领域知识得到
# 不同领域内,遇到不同的问题,产参数一般不同;
# 领域:如自然语言处理、视觉搜索等;
2、经验数值
# 一般机器学习算法库中,会封装一些默认的超参数,这些默认的超参数一般都是经验数值;
# kNN算法这scikit-learn库中,k值默认为5,5就是在经验上比较好的数值;
3、通过试验搜索得到
- 思路:将不同的超参数输入模型,选取准确度最高的超参数;
- 试验搜索也称为网格搜索:对不同的超参数,使用对个for语句,逐层搜索;
- 试验搜索过程:以kNN算法为例;
# 在Jupyter NoteBook中实现的代码 import numpy as np from sklearn import datasets digits = datasets.load_digits() X = digits.data y = digits.target from ALG.train_test_split import train_test_split X_train, X_test, y_train, y_test = train_test_split(X, y, test_train = 0.2) # 1)按经验选定超参数k = 5 from sklearn.neighbors import KNeighborsClassifier knn_clf = KNeighborsClassifier(n_neighbors = 5) knn_clf.fit(X_train, y_train) knn_clf.score(X_test, y_test) # 2)按试验搜索,获取最优的超参数K,不考虑weights best_score = 0.0 best_k = -1 for k in range(1, 11): knn_clf = KNeighborsClassifier(n_neighbors = k) knn_clf.fit(X_train, y_train) knn_score = knn_clf.score(X_test, y_test) if knn_score > best_score: best_score = knn_score best_k = k print("best_k = ", best_k) print("best_score = ", best_score) # 3)按试验搜索,获取最优的超参数k、weight best_method = "" best_score = 0.0 best_k = -1 for method in ["uniform", "distance"]: for k in range(1, 11): knn_clf = KNeighborsClassifier(n_neighbors = k) knn_clf.fit(X_train, y_train) knn_score = knn_clf.score(X_test, y_test) if knn_score > best_score: best_score = knn_score best_k = k best_method = method print("best_mrthod = ", best_method) print("best_k = ", best_k) print("best_score = ", best_score) # 4)试验搜索,获取最优产参数k、P(weights必须为distance) %%time best_p = -1 best_score = 0.0 best_k = -1 for k in range(1, 11): for p in range(1, 6): knn_clf = KNeighborsClassifier(n_neighbors = k, weights = "distance", p = p) knn_clf.fit(X_train, y_train) knn_score = knn_clf.score(X_test, y_test) if knn_score > best_score: best_score = knn_score best_k = k best_p = p print("best_p = ", best_p) print("best_k = ", best_k) print("best_score = ", best_score)
5)其它
- ** 一般不同的超参数决定了不同的分类的准确率,它们之间呈连续变化;如果最终找到的最优的超参数为范围的边界值,意味着可能有更优的取值在边界的外面,所以要拓展搜索范围重新查询最优的超参数;
- 以上代码包含了调用scikit-learn库内的算法:导入模块、实例化、fit、调参(选取最优超参数)、预测
三、模型参数
# 模型参数:算法过程中学习的参数;
# kNN算法中没有模型参数,因为它没有模型;
# 线性回归算法和逻辑回归算法,包含有大量的模型参数;
# 什么是模型选择?
四、距离推导
- 欧拉距离:math.sqrt(np.sum((X1 - X2) ** 2)),向量X1与向量X2的欧拉距离;
- 曼哈顿距离:np.sum(|X1 - X2|),向量X1与向量X2的曼哈顿距离;
- 明科夫斯基距离:由欧拉距离和曼哈顿距离推到出;
- 下图从上至下:曼哈顿距离、欧拉距离、明科夫斯基距离;
- 在明科夫斯基距离中:
- 当P = 1,明科夫斯基距离 == 曼哈顿距离;
- 当P = 2,明科夫斯基距离 == 欧拉距离;
- 当P >= 3,对应的明科夫斯基距离为其它距离;
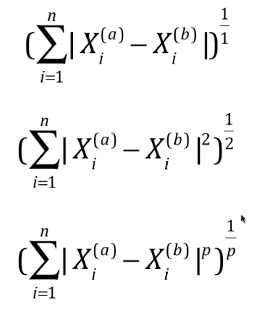





· 10年+ .NET Coder 心语,封装的思维:从隐藏、稳定开始理解其本质意义
· .NET Core 中如何实现缓存的预热?
· 从 HTTP 原因短语缺失研究 HTTP/2 和 HTTP/3 的设计差异
· AI与.NET技术实操系列:向量存储与相似性搜索在 .NET 中的实现
· 基于Microsoft.Extensions.AI核心库实现RAG应用
· 阿里巴巴 QwQ-32B真的超越了 DeepSeek R-1吗?
· 10年+ .NET Coder 心语 ── 封装的思维:从隐藏、稳定开始理解其本质意义
· 【译】Visual Studio 中新的强大生产力特性
· 【设计模式】告别冗长if-else语句:使用策略模式优化代码结构
· 字符编码:从基础到乱码解决