数据挖掘：数据（数据的基本统计描述）

一、概述

1. 对应成功的数据预处理而言，把握数据的全貌至关重要。
2. 基本统计描述可以用来识别数据的性质，凸显哪些数据值应该视为噪声或离群点。

 

二、中心趋势度量：均值、中位数、众数、中列数

• 也就是度量数据分布的中部或中心位置。（给定一种属性，它的值大部分落在何处）
• 频率：区间内数值的个数。

　1）均值（mean）

• 数据集“中心”的最常用、最有效的数值度量是均值。
• 均值对应于关系数据库系统提供的内置聚集函数 average（SQL 的 avg() ）。

• 加权平均值或加权平均

1. 加权（ω）：即权重，反应它们所依附的对应值的意义、重要性或出现的频率。
2. 计算：x_mean = ( ω₁x₁ + ω₂x₂ + ... +ω_Nx_N ) / ( ω₁ + ω₂ + ... + ω_N )

• 缺点
• 对极端值（例如：离群点）很敏感。（例如，公司的平均薪水会被少数几个高收入的经理显著推高）

• 方法
• 使用截尾均值：丢弃高低极端值后的均值。

　2）中位数（median）

• 定义：有序数据值的中间值。

• 计算：N 个数值，若 N 是奇数，第 (N + 1) / 2 个数据为中位数，若 N 是偶数，则中位数不唯一，它是最中间的两个值和它们之间的任意值（在数值属性的情况下，中位数取最中间连个值的平均值）。

• 特点

1. 主要度量倾斜（非对称）数据。
2. 把数据较高的一半与较低的一半分开的值。

•  当数据集中值的数量很大时，中位数的计算：
• 思路：用插值计算整个数据集的中位数的近似值；（将数据集划分为多个区间（如，1~1000、1001~2000、2001~3000））
• median = L₁ + (( N/2 - (Σfreq)_l ) / freq_median ) width

1. median：整个数据集的中，该种属性的中位数；
2. L₁ ：中位数区间（包含中位数频率的区间，也就是包含中位数所在位置的区间）的下限（最小值）；
3. N：整个数据集中数值的个数；
4. (Σfreq)_l：低于中位数区间的的所有区间的频率的和；（也就是在中位数区间以后的所有区间中数值的数量的总和）
5. freq_median：中位数区间的频率；（中位数所在区间的数值的个数）
6. width：中位数区间的宽度（区间的最大值与最小值的差）；

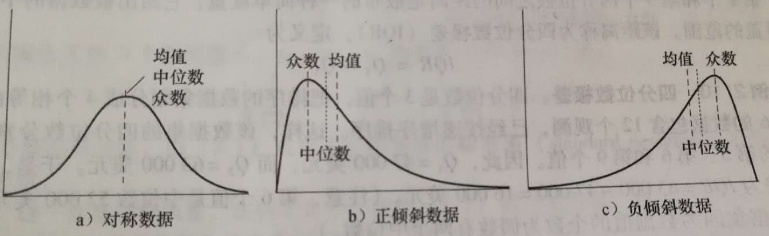
　3）众数（mode）

• 众数：数据集中出现频率最多的值；
• 最高频率对应多个值时，会有多个众数；
• 具有一个、两个、三个众数的数据集合，分别称为单峰的（unimodal）、双峰的（bimodal）、三峰的（trimodal）。
• 一般具有两个或更多众数的数据集是多峰的（multimodal）。
• 如果数据集中每个数值只出现一次，该数据集没有众数。
• 对于适度倾斜（非对称）的单峰数值数据，经验关系：mean - mode ≈ 3 X ( mean - median ) ；（也就是，如果均值和中位数已知，则适度倾斜的单峰频率曲线的众数容易近似计算）

　4）中列数（midrange）

• 中列数：数据集中最大值和最小值的平均值，也可以用来评估数值数据的中性趋势。（中列数容易使用 SQL 的聚集函数 max() 和 min() 计算）

　5）其它

•  

 

三、度量数据散布：极差（range）、四分位数（quartile）、方差（variance）、标准差（standard  deviation）、四分位极差（IQR）

• 作用：有助于找出离群点。
• 观测值：指被分析的数据集中的数值；

　1）极差、四分位数、四分位数极差

• 极差：数据集中最大值和最小值的差。
• 分位数：取至数据分布的每隔一定间隔上的点，把数据划分成基本上大小相等的连贯集合。（说是基本上，因为可能不存在把数据划分成恰好大小相等的诸子集的X的数据值）
• 四分位数：第 N/4（Q₁）、第 N/2（Q₂，也即是中位数）、第3N/4（Q₃） 的数，将数据划分为4份。（N表示数据集的数值的总个数）
• 四分位数极差：IQR = Q₃ - Q_1；

　2）五数概括（five-number summary）、盒图、离群点

• 对于描述倾斜分布，不能使用单个散布数值度量。
• 识别离群点的方法：挑选落在 Q₃ 以上或 Q₁ 以下至少 1.5IQR处的值。
• 五数概括：不仅使用 Q₁、中位数、Q₃，同时提供最高和最低数据值。（共5个数）

• 盒图（boxplot）
• 盒图可以用来比较若干个可比较的数据集。
• 描述数据分布的直观表示，体现了五数概括：

1. Q₁、Q₃、IQR：盒（实线长方形）的端点一般在四分位数上，使得盒图长度是四分位数的极差 IQR；
2. 中位数：中位数用盒图的线表示；
3. 胡须：盒外的两条线（与虚线相连的两条线，称作胡须）延伸到最小（Minimum）和最大（Maximum）观测值（观测值：被分析的数据集中的所有数值）；（胡须延伸处的最大为 Q₃ + 1.5IQR，最小为Q₁ - 1.5IQR，超出范围的视为离群点）、（胡须的末端必须是观测值，也就是说，胡须的末端不一定等于 Q₃+1.5IQR 或 Q₁-1.5IQR）
4. 离群点：处于胡须外的观测值；（仅当最高和最低观测值超过四分位数不到 1.5IQR 时，胡须扩展到它们（离群点），否则，胡须在出现在四分位数的 1.5IQR 之内的最极端的观测值处终止，剩下的情况个别的绘出）

　3）方差、标准差

• 作用：方差和标准差都是数据分布度量，指出数据分布的散布程度；
• 低标准差意味着数据观测趋向于非靠近均值，高标准差表示数据分布在一个大的值域内；
• 

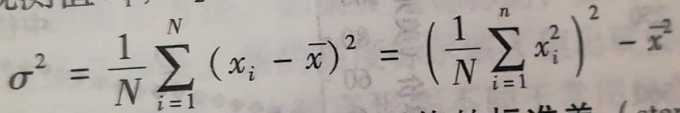
1. σ²：方差；
2. σ：标准差；

• 标准差的性质：

1. σ 度量关于均值的发散，仅当选择均值作为中心度量时使用；
2. 仅当不存在发散时，即当所有的观察值都均有相同值时，σ = 0；否则，σ > 0；
3. 一般，一个观测值远离均值不会超过数倍个标准差。（也就是说： X_观察值 - mean ≠ nσ）

• 大型数据库中，方差和标准差的计算是可伸缩的。

 

四、数据的基本统计描述的图形显示

•  描述方法：分位数图（quatile plot）、分位数-分位数图（quantile-quantile  plot）、直方图、散点图。
• 作用：有助于可视化的审视数据，并有助于数据预处理。
• 显示一元分布（一个属性的数据）：分位数图、分位数-分位数图、直方图。
• 显示二元分布（涉及两个属性）：散点图。

　1）分位数图

• 作用：观察一组数据，不同分位数时的分布状态。（一个分位数反应 f_i X 100% 比例的数据的分布状态）
• 特点：

1. 观察单变量数据分布。
2. 显示给定属性的全部数据。
3. 绘出了分位数信息。（根据不同的分位数  f_i 观察数据的分布）

• 绘制方法

1. 在分位数图中，一个 x_i 对应一个分位数 f_i 。
2. f_i = (i - 0.5) / N；
3. 

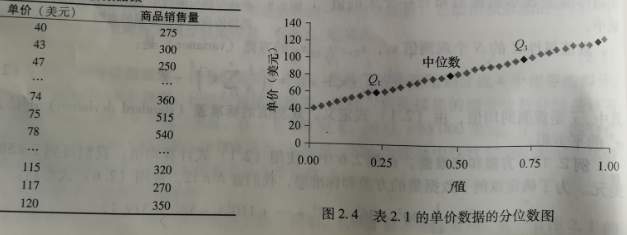
 　2）分位数-分位数图