牛客寒假算法基础训练营1

牛客寒假集训营一

Easy

A-DFS搜索

#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 10;
#define int long long

void solve()
{
    int n ;
    cin >> n;
    
    string s;
    cin >> s;
    
    map<char , bool>mp1;
    map<char , bool>mp2;
    bool st_d = false;
    bool st_D = false;
    
    for(int i = 0 ; i < s.size() ; i ++)
    {
        if(s[i] == 'd') st_d = true;
        if(s[i] == 'D') st_D = true;
        
        if(s[i] == 'f' && st_d) mp1[s[i]] = true;
        if(s[i] == 'F' && st_D) mp2[s[i]] = true;
        
        if(s[i] == 's' && mp1['f']) mp1[s[i]] = true;
        if(s[i] == 'S' && mp2['F']) mp2[s[i]] = true;
        
        if(mp1['s'] && mp2['S']) break;
    }
    
    if(mp2['S']) cout << 1 << " ";
    else cout << 0 << " ";
    
    if(mp1['s']) cout << 1 << endl;
    else cout << 0 << endl;
    
}

signed main()
{
    int xiao_p;
    cin >> xiao_p;

    while(xiao_p --)
    {
        solve();
    }

    return 0;
}

M-牛客老粉才知道的秘密

#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 10;
#define int long long

void solve()
{
    int n;
    cin >> n;
    
    while(n --)
    {
        int x;
        cin >> x;
        
        int ans = 0;
        int res = x - 6;
        ans += (res + 5) / 6; //向右
        if(x % 6 == 0) cout << x /6 << endl;
        else
        cout << ans * 2 << endl;
    }
}

signed main()
{
    int xiao_p;
    xiao_p = 1;

    while(xiao_p --)
    {
        solve();
    }

    return 0;
}

Mid-easy

C-按闹分配

当鸡插队的时候 ，鸡后面每个人完成任务的时间都会推迟 tc 分钟，所以 总的不满意度增加的就是 tc*(鸡后面的人数)，

我们给出了 最大不满意度为M，所以我们可以求出来 排在鸡后面的人数就是为 M / tc (下取整)

我们要求 最快鸡能多久完成他的任务，只需要算鸡前面的人的总是间 再加上鸡的就是答案

#include <bits/stdc++.h>
using namespace std;
const int N = 1e8 + 10;
typedef long long LL;
LL pre[N];

int main()
{
    LL n , q , t;
    cin >> n >> q >> t;
    
    for(int i = 1 ; i <= n ; i ++) cin >> pre[i];
    
    sort(pre + 1 , pre + 1 + n);
    
    for(int i = 1 ; i <= n ; i ++) pre[i] += pre[i - 1];
    
    while(q --)
    {
        LL x;
        cin >> x;
        
        LL pos = x / t;
        
        cout << pre[max((LL)0 , n-pos)] + t << endl;
    }

    return 0;
}

B-关鸡

要将情况讨论完整

#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 10;
#define int long long

void solve()
{
    int n;
    cin >> n;

    unordered_map<int , int>mp1 , mp2;

    //左边是否堵住 右边是否堵住 ， 左边有火 ， 右边有火
    bool l_blocked , r_blocked , l_fire , r_fire;
    l_blocked = r_blocked = l_fire = r_fire = false;

    for(int i = 1 ; i <= n ; i ++)
    {
        int r , c;
        cin >> r >> c;

        if(r == 1) mp1[c] = 1;
        else if(r == 2) mp2[c] = 1;
    }

    //遍历第一行
    for(auto u : mp1)
    {
        int t = u.first;
        if(t > 0) r_fire = true;
        else if(t < 0) l_fire = true;

        if(t < 0)
        {
            if(mp2[t] || mp2[t - 1] || mp2[t + 1]) l_blocked = true; //判断左边是否被堵住;
        }
        else if(t > 0)
        {
            if(mp2[t] || mp2[t - 1] || mp2[t + 1]) r_blocked = true;//判断右边是否被堵住
        }
    }

    //单独判断一下第二行 左右两边是否有火;
    for(auto u : mp2)
    {
        int t = u.first;
        if(t > 0) r_fire = true;
        else if(t < 0) l_fire = true;
    }

    int ans;

    //鸡下面有火
    if(mp2[0])
    {
        if(l_blocked && r_blocked) ans = 0; //左右堵住
        else if(mp1[1] && mp1[-1]) ans = 0;//鸡相邻两边堵住
        else if(mp1[1] && l_blocked) ans = 0;//鸡相邻右边堵住，左边堵住
        else if(mp1[-1] && r_blocked) ans = 0;//鸡相邻左边堵住，右边堵住
        else if(mp1[1] || mp1[-1] || l_blocked || r_blocked) ans = 1;
        //鸡相邻左边 或 相邻右边 或 左边堵住 或 右边堵住
        else  ans = 2; //其余情况 都是2
    }
    //鸡下面 无火
    else 
    {
        if(l_blocked && r_blocked) ans = 0; //左右堵住；
        else if(l_blocked && r_fire) ans = 1; //左边堵住, 右边有火
        else if(r_blocked && l_fire) ans = 1;//右边堵住，左边有火
        else if(mp1[1] && mp1[-1]) ans = 1; //鸡相邻左右堵住 ；
        else if(mp1[1] || mp1[-1]) ans = 2; //鸡相邻 左边 或 右边 堵住;
        else if(l_blocked && !r_fire) ans = 2; //左边堵住，右边无火
        else if(r_blocked && !l_fire) ans = 2; //右边堵住，左边无火；
        else if(r_fire && l_fire) ans = 2; //左边有火 ， 右边有火
        else ans = 3;
    }

    cout << ans << endl;
    
}

signed main()
{
    int xiao_p;
    cin >> xiao_p;

    while(xiao_p --)
    {
        solve();
    }

    return 0;
}

E-本题又主要考察了贪心

数据量很小，可以用dfs直接 暴力搜索

#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 10;
#define int long long
typedef pair<int, int>PII;
int point[N];
PII test[N];
int n , m;
int res = 2e9;

void dfs(int u, int num)
{
    if(num > m)
    {
        int pos = 1;
        for(int i = 1 ; i <= n ; i ++)
        {
            if(point[i] > point[1]) pos ++;
        }
        
        res  = min(res , pos); 
        return;
    }
    
    int a = test[u].first;
    int b = test[u].second;
    
    if(a == 1)
    {
        point[a] += 3;
        dfs(u + 1 , num + 1);
        point[a] -= 3;
    }
    else
    {
        point[a] += 3;
        dfs(u + 1 , num ++);
        point[a] -= 3;
    
        point[a] ++;
        point[b] ++;
        dfs(u + 1 , num ++);
        point[a] --;
        point[b] --;
    
        point[b] += 3;
        dfs(u + 1 , num ++);
        point[b] -= 3;
    }
}

void solve()
{
    cin >> n >> m;
    
    for(int i = 1 ; i <= n ; i ++) cin >> point[i];
    
    for(int i = 1 ; i <= m ; i ++)
    {
        int a , b;
        cin >> a >> b;
        if(a > b) swap(a , b);
        test[i] = {a , b};
    }
    
    dfs(1 , 1);
    
    cout << res << endl;
}

signed main()
{
    int xiao_p;
    cin >> xiao_p;

    while(xiao_p --)
    {
        solve();
    }

    return 0;
}

G-why买外卖

\[每次将优惠的价格 算一遍 前缀和，我们索要支付的价格就是 a_i - pre_i(前面优惠的价格的总和)\\ 只要这个索要支付价格小于我们有的钱m就说明 可以使用到这张优惠卷，那我们原价能买的东西，所耗费钱最大 为m + pre_i\\ 购买东西最大成本=手里的钱 \ +优惠的钱 \\ ans = m + pre_i \]

#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 10;
#define int long long
#define f first
#define s second
typedef pair<int , int>PII;
typedef long long LL;
int n , m;
int pre[N];

void solve()
{
    cin >> n >> m;
    vector<PII>p(n + 1);
    for(int i = 1 ; i <= n ; i ++)
    {
        cin >> p[i].f >> p[i].s;
    }
    
    sort(p.begin() , p.end());
    
    
    
    for(int i = 1 ; i <= n ; i ++) pre[i] = pre[i - 1] + p[i].s;

    int ans = m;

    for(int i = 1 ; i <= n ; i ++)
    {
        if(p[i].f - pre[i] <= m) ans = max(ans , m + pre[i]);
    }

    cout << ans << endl;
}

signed main()
{
    int xiao_p;
    cin >> xiao_p;

    while(xiao_p --)
    {
        solve();
    }

    return 0;
}

Mid

L-要有光

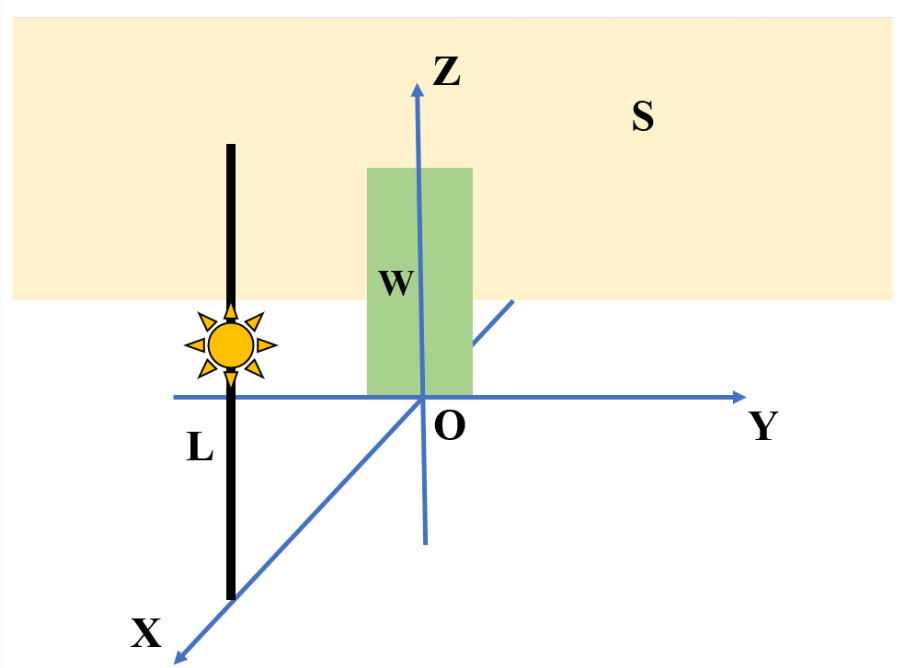
只需要让 光源 沿着绿墙 照到白墙 上面， 使得绿墙的长度为 三角形的中位线，然后算出 梯形的面积 即可；（找特殊）

#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 10;
#define int long long
int n , m;
void solve()
{
    int c , d, h , w;
    cin >> c >> d >> h >> w;
    
    cout << (long long)3 * w * c<< endl;

}

signed main()
{
    int xiao_p;
    cin >> xiao_p;

    while(xiao_p --)
    {
        solve();
    }

    return 0;
}

D-数组成鸡

这个要判断的数 x 范围是在1e9 以内的，所以我们 只需要预处理 出来 乘积大于1e9 那么一定不可能；

我们知道2^30次方 大于1e9 ， 也就是说 ，绝对值大于1的数 如果大于30个 那么乘积 一定大于了 1e9，一定不可能；

但我们可以通过加减操作 来进行 变大或者变小，在判断 是否能 得出 x；

所以我们进行分类；

#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 10;
#define int long long
#define f first
#define s second
#define endl '\n'

void solve()
{    
    int n , m;
    cin >> n >> m;
    map<int,int>cnt; //存每个数出现的次数
    set<int>ans; //将合法数字存进去,最后判断；
    ans.insert(0);
    vector<int> a(n);
    
    for(int i = 0 ; i < n ; i ++)
    {
        cin >> a[i];
        cnt[a[i]] += 1; //存一个数 出现的次数
    }
    //分类讨论
    if(n >= 30)
    {
        for(auto [x , y] : cnt)
        {
            if(n - cnt[x] - cnt[x - 2] > 30) continue;  
            //我们将这个数变为绝对值变为1，同时需要考虑比他小2的数会变成-1，绝对值也为1，所以要将这两个的总数都要减去；
            //如果数量还是大于30那么就不可能凑成，直接continue；
            
            
            //如果小于30才有可能不超过1e9
            //进行判断；
            int mul = 1;
            bool ok = true;
            
            for(int i = 0 ; i < n ; i ++)
            {
                mul = mul * (a[i] - (x - 1)); //减去变为1 //因为 要将那个数变为1，就需要让每个数减去这个数 - 1；
                if(abs(mul) > 1e9) //如果绝对值大于1e9就break; //如果大于1额就break
                {
                    ok = false;
                    break;
                }
            }
            if(ok) ans.insert(mul); //如果不大于1e9，就把答案放进ans里面;

            mul = 1;
            ok = true;

            for(int i = 0 ; i < n ; i ++)
            {
                mul = mul * (a[i] - (x + 1)); //这是将某个数变为-1的情况，也就是减去这个数+1；
                if(abs(mul) > 1e9)
                {
                    ok = false;
                    break;
                }
            }
            if(ok) ans.insert(mul);
        }
    }
    //n小于30的情况
    else
    {
        //我们知道如果两个数同时大于1e4.5 那么乘积就会超过1e9
        //所以我们枚举从-1e5 到 1e5
        //进行枚举；
        //排序后，将最小的数变为0，也就是让所有数，减去最小的数，在进行枚举；
        sort(a.begin() , a.end());
        int temp = a[0];
        
        for(int i = 0 ; i < n ; i ++) a[i] -= temp;
        
        //当最小的那个数为1e5的时候，可以保证 后面的所有数都大于1e5，乘积一定超过1e9，
        //在枚举过程中，他的所有情况都已经算过了；
        //但当最小的数为-1e5的时候，没法保证，所以这一段只能保证上线，
        for(int i = -1e5 ; i <= 1e5 ; i ++)
        {
            int mul = 1;
            bool ok = true;
            for(int j = 0 ; j < n ; j ++)
            {
                mul = mul * (a[j] + i);
                if(abs(mul) > 1e9)
                {
                    ok = false;
                    break;
                }
            }
            
            if(ok) ans.insert(mul);
        }
        
        //这一段 就是枚举的下线；
        //我们将数组从大到小排序，让所有的数减去最大的数
        //那么当最大的数为-1e5的时候 后面所有的数都小于-1e5， 乘积绝对值肯定 大于1e9，
        //其余同理上面
        reverse(a.begin() , a.end());
        
        temp = a[0];
        
        for(int i = 0 ; i < n ; i ++) a[i] -= temp;
        
        for(int i = -1e5; i <= 1e5 ; i ++)
        {
            int mul = 1;
            bool ok = true;
            for(int j = 0 ; j < n ; j ++)
            {
                mul = mul * (a[j] + i);
                if(abs(mul) > 1e9)
                {
                    ok = false;
                    break;
                }
            }
            
            if(ok) ans.insert(mul);
        }
    }

    while(m --)
    {
        int x;
        cin >> x;

        if(ans.count(x))
        cout << "Yes" << endl;
        else cout << "No" << endl;
    }
}

signed main()
{
    int xiao_p;
    xiao_p = 1;
    ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
    while(xiao_p --)
    {
        solve();
    }

    return 0;
}

I-It's bertrand paradox. Again!_

很离谱的一道题，这个方法正确的原因在于，两种方法的概率是不一样的，均值是不同的；我们需要自己生成数据然后判断这个均值的大小，然后再进行判断：

（参考up主Turing_Sheep）

#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 10;
#define int long long
#define endl '\n'
#define pair<int,int>PII
//随机数引擎来进行生成随机数
uniform_int_distribution<int> u1(-99,99);//生成圆心
uniform_int_distribution<int> u2(1,100);//生成半径
default_random_engine e;

void solve()
{
    int n = 100;
	double r1 = 0;
    //模拟第一个过程，当r不满足时，我们重新生成r
	for(int i = 1; i <= n; i ++){

		int x = u1(e), y = u1(e);
		while(1){
			int r = u2(e);
			if(x + r > 100 || x - r < -100 || y + r > 100 || y - r < -100){
				continue;
			}else{
				r1 += (abs(x) + abs(y));
				break;
			}
		} 
		
	}
    
    //模拟第二个过程，当r不满足时候，重新生成x, y, r；
	double r2 = 0;
	for(int i = 1; i <= n; i ++){
		while(1){
			int x = u1(e), y = u1(e);
			int r = u2(e);
			if(x + r > 100 || x - r < -100 || y + r > 100 || y - r < -100){
				continue;
			}else{
				r2 += (abs(x) + abs(y));
				break;
			}
		} 
	}
	r1 = r1 / n;
	r2 = r2	/ n;
	cout << r1 << " " << r2 << endl;
}

signed main()
{
    e.seed(time(NULL)); //随机数种子
    int xiao_p;
    cin >> xiao_p;
    ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);

    while(xiao_p --)
    {
        solve();
    }

    return 0;
}

#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 10;
#define int long long
typedef pair<int,int> PII;

void solve()
{
    int n;
    cin >> n;

    int sum = 0;

    for(int i = 1 ; i <= n ; i ++)
    {
        int x , y , r;
        cin >> x >> y >> r;

        sum += (abs(x) + abs(y));
    }

    if((sum / n) > 90) cout << "bit-noob" << endl;
    else cout << "buaa-noob" << endl;
}

signed main()
{
    int xiao_p;
    xiao_p = 1;
    ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);

    while(xiao_p --)
    {
        solve();
    }

    return 0;
}

F-鸡数题

\[根据3条件 :2^n - 1这个二进制的数 我们可以知道 一共有n个1，\\ 根据4条件 :当i \not= j时，a_i \& a_j = 0,代表着二进制的这些数里面的每一位 只能存在一个1\\ 并且在排序过后，是单调递增的情况\\ 所以这个问题我们就可以转化成将每个不同位置上，共有n个1 分到 m个数里面，并且这些数二进制里面的每一位，只能存在一个1\\ 再换句话将，就是将n个不同小球，分到m个相同盒子里面的方案数，也就是第二类斯特林数； \]

\[S(n,m) = \frac{1}{m!}\ *\ \sum_{k=0}^{m}(-1)^kC(m,k)(m-k)^n\\ 化简得到\\ \sum_{k=0}^{m}\frac{(-1)^k\ *\ (m-k)^n}{(m-k)!\ *\ k!}mod\ (1e9 + 7)\\ 根据费马小定理和快速幂求逆元\\ \sum_{k=0}^{m}\ (-1)^k\ *\ (m-k)^n\ *\ ((m-k)!)^{-1}\ *\ (k!)^{-1} \]

#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 10 , mod = 1e9 + 7;
#define int long long
typedef pair<int,int> PII;
#define end '\n'
int f[N] , nf[N]; //求阶乘;
int qmi(int a , int b) //快速幂求逆元
{
    int res = 1;

    while(b)
    {
        if(b & 1) res = res * a % mod;

        a = a * a % mod;

        b >>= 1;
    }

    return res;
}
//根据逆元 求组合数；
void solve()
{
    int n , m;
    cin >> n >> m;
    f[0] = nf[0] = 1;

    for(int i = 1 ; i < N ; i ++) //预处理阶乘逆元
    {
        f[i] = f[i - 1] * i % mod;
        nf[i] = nf[i - 1] * qmi(i , mod - 2) % mod;
    }

    int ans = 0;

    for(int k = 0 ; k <= m ; k ++)
    {
        if(k % 2 == 0)
        {
            ans = (ans + qmi(m - k , n) * nf[m - k] % mod * nf[k] % mod + mod) % mod;
            
        } 
        else 
        {
            ans = (ans - (qmi(m - k , n) * nf[m - k] % mod * nf[k] % mod)) % mod;
        }
    }

    cout << ans << endl;

}

signed main()
{
    int xiao_p;
    xiao_p = 1;
    ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);

    while(xiao_p --)
    {
        solve();
    }

    return 0;
}