[CodeForces940E]Cashback(set+DP)
Description
Since you are the best Wraith King, Nizhniy Magazin «Mir» at the centre of Vinnytsia is offering you a discount.
You are given an array a of length n and an integer c.
The value of some array b of length k is the sum of its elements except for the 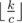 smallest. For example, the value of the array [3, 1, 6, 5, 2] with c = 2 is 3 + 6 + 5 = 14.
smallest. For example, the value of the array [3, 1, 6, 5, 2] with c = 2 is 3 + 6 + 5 = 14.
Among all possible partitions of a into contiguous subarrays output the smallest possible sum of the values of these subarrays.
Solution
这里有一个贪心的思想,就是只需要划分长度为1或者长度为c的区间,其他的不会比这两种更优
首先裸的DP,\(dp[i]=min\{dp[j]+Cost_{j+1,i}\}\)
然后只要对长度为c的区间进行更新,可以用multiset进行存储数据
(STL中的multiset与set的区别在于可以存储相同的元素)
具体见代码
Code
#include <cstdio>
#include <algorithm>
#include <set>
#define ll long long
#define N 100010
using namespace std;
int n,c;
ll A[N],dp[N],sum;
multiset<ll> q;//默认升序排列
int main(){
scanf("%d%d",&n,&c);
for(int i=1;i<=n;i++)scanf("%I64d",&A[i]);
for(int i=1;i<=n;i++){
sum+=A[i];
dp[i]=dp[i-1]+A[i];
q.insert(A[i]);
if(i>c){q.erase(q.find(A[i-c]));sum-=A[i-c];}//删除最小的元素
if(i>=c){dp[i]=min(dp[i],dp[i-c]+sum-*q.begin());}//转移
}
printf("%I64d\n",dp[n]);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号