HDU1255——覆盖的面积（线段树+离散+扫描线）

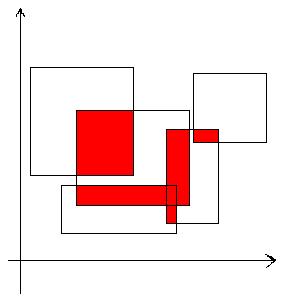
给定平面上若干矩形,求出被这些矩形覆盖过至少两次的区域的面积.

Input

输入数据的第一行是一个正整数T(1<=T<=100),代表测试数据的数量.每个测试数据的第一行是一个正整数N(1<=N<=1000),代表矩形的数量,然后是N行数据,每一行包含四个浮点数,代表平面上的一个矩形的左上角坐标和右下角坐标,矩形的上下边和X轴平行,左右边和Y轴平行.坐标的范围从0到100000.

注意:本题的输入数据较多,推荐使用scanf读入数据.

Output

对于每组测试数据,请计算出被这些矩形覆盖过至少两次的区域的面积.结果保留两位小数.

Sample Input

2
5
1 1 4 2
1 3 3 7
2 1.5 5 4.5
3.5 1.25 7.5 4
6 3 10 7
3
0 0 1 1
1 0 2 1
2 0 3 1

Sample Output

7.63
0.00

题解：

与这一题类似，建议先搞懂这一题：海克斯传送门

如果搞懂了上面那道题，这道题就很简单了，基本一模一样，只需要把条件

if（Tree[temp].cnt)改成if(Tree[temp].cnt>1)就行了。

代码：

#include <bits/stdc++.h>

using namespace std;

const int MAXN = 2005;

struct Node{
	double l,r,h;
	int flag;
	Node(){}
	Node(double a,double b,double c,int d): l(a),r(b),h(c),flag(d){}  
	bool operator < (const struct Node &b)const{ 
		return h < b.h;
	}
}node[MAXN];

struct D{
	double value;
	int cnt;
	bool lazy;
}Tree[MAXN*4];

double X[MAXN];

int Bin(double key , int Num){
	int l = 1,r = Num,mid;
	while(l<=r){
		mid = l + (r-l)/2;
		if(X[mid] == key)return mid;
		else if(X[mid] > key)r = mid-1;
		else if(X[mid] < key)l = mid+1;
	}
	return -1;
}

void Build(int temp , int left , int right){
	Tree[temp].cnt = 0;
	Tree[temp].value = 0.0;
	Tree[temp].lazy = false;
	if(left == right)return;
	int mid = left + (right-left)/2;
	Build(temp<<1,left,mid);
	Build(temp<<1|1,mid+1,right);
}

void PushDown(int temp , int left , int right){
	if(Tree[temp].lazy){
		Tree[temp<<1].cnt = Tree[temp<<1|1].cnt = Tree[temp].cnt;
		Tree[temp<<1].lazy = Tree[temp<<1|1].lazy = true;
		int mid = left + (right-left)/2;
		if(Tree[temp].cnt>1){
			Tree[temp<<1].value = X[mid+1]-X[left];
			Tree[temp<<1|1].value = X[right+1]-X[mid+1];
		}
		else Tree[temp<<1].value = Tree[temp<<1|1].value = 0;
		Tree[temp].lazy = false;
	}
}

void Up(int temp){
	if(Tree[temp<<1].cnt==-1 || Tree[temp<<1|1].cnt==-1 || Tree[temp<<1].cnt!=Tree[temp<<1|1].cnt)Tree[temp].cnt = -1;
	else Tree[temp].cnt = Tree[temp<<1].cnt;
	Tree[temp].value = Tree[temp<<1].value + Tree[temp<<1|1].value;
}

void Updata(int temp , int left , int right , int ql , int qr ,int flag){
	if(ql>right || qr<left)return ;
	if(ql<=left && qr>=right){
		if(Tree[temp].cnt != -1){
			Tree[temp].cnt += flag;
			Tree[temp].lazy = true;
			if(Tree[temp].cnt>1)Tree[temp].value = X[right+1]-X[left];
			else Tree[temp].value = 0;
			return ;
		}
	}
	PushDown(temp,left,right);
	int mid = left + (right-left)/2;
	if(ql<=mid)Updata(temp<<1,left,mid,ql,qr,flag);
	if(qr>mid)Updata(temp<<1|1,mid+1,right,ql,qr,flag);
	Up(temp);
}

int main(){
	int N,T;
	scanf("%d",&T);
	double x1,x2,y1,y2;
	double ans;
	while(T--){
		scanf("%d",&N);
		ans = 0.0;//最终面积 
		int n = 0,m = 0;
		for(int _=0 ; _<N ; _++){
			scanf("%lf %lf %lf %lf",&x1,&y1,&x2,&y2);
			X[++n] = x1;
			node[++m] = Node(x1,x2,y1,1);
			X[++n] = x2;
			node[++m] = Node(x1,x2,y2,-1);
		}
		sort(X+1,X+1+n);
		sort(node+1,node+1+m);
		int sum = 1;
		for(int i=2 ; i<=n ; i++)if(X[i]!=X[i-1])X[++sum] = X[i];
		Build(1,1,sum-1);
		for(int i=1 ; i<=m ; i++){
			int l = Bin(node[i].l,sum);
			int r = Bin(node[i].r,sum)-1;
			Updata(1,1,sum-1,l,r,node[i].flag);
			ans += Tree[1].value*(node[i+1].h-node[i].h);
		}
		printf("%.2lf\n",ans);  
	}
	
	return 0;
}