hdu1828 Picture(线段树+离散化+扫描线+基础周长并模板)两种方法
A number of rectangular posters, photographs and other pictures of the same shape are pasted on a wall. Their sides are all vertical or horizontal. Each rectangle can be partially or totally covered by the others. The length of the boundary of the union of all rectangles is called the perimeter.
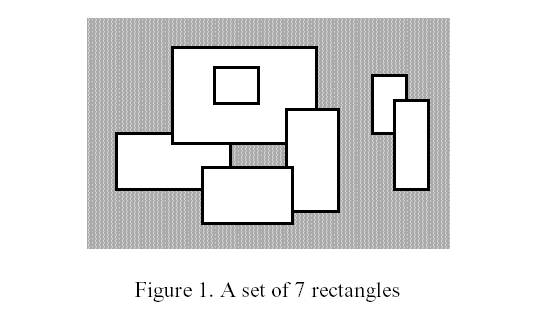
Write a program to calculate the perimeter. An example with 7 rectangles is shown in Figure 1.
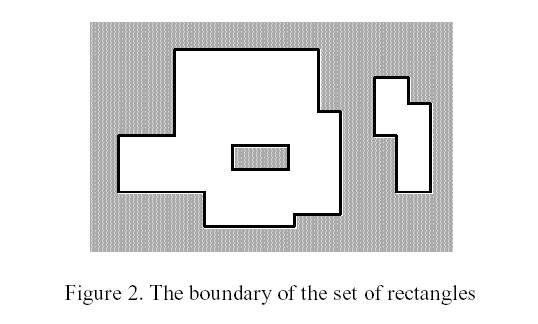
The corresponding boundary is the whole set of line segments drawn in Figure 2.
The vertices of all rectangles have integer coordinates.
Input
Your program is to read from standard input. The first line contains the number of rectangles pasted on the wall. In each of the subsequent lines, one can find the integer coordinates of the lower left vertex and the upper right vertex of each rectangle. The values of those coordinates are given as ordered pairs consisting of an x-coordinate followed by a y-coordinate.
0 <= number of rectangles < 5000
All coordinates are in the range [-10000,10000] and any existing rectangle has a positive area.
Output
Your program is to write to standard output. The output must contain a single line with a non-negative integer which corresponds to the perimeter for the input rectangles.
Sample Input
7 -15 0 5 10 -5 8 20 25 15 -4 24 14 0 -6 16 4 2 15 10 22 30 10 36 20 34 0 40 16
Sample Output
228
方法一：
做两次扫描线。第一次是从下向上，第二次是从左向右，这样就能得到四周的周长
其次每次增加线段后，把新得到的长度与之前的做比较，两者之差的绝对值就是这次增加线段后的长度
所以每次都这样更新，最后得到的就是周长了。
代码：
PS：这个代码用编译器用c++能过，用G++就WA了，不知道为啥。。。
这种涉及编译器内部优化方式和命名的问题我也是一点法没有。。。
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
const int MAXN = 5005;
struct Line{
int l,r,h,v;
Line(){}
Line(int a,int b,int c,int d):l(a),r(b),h(c),v(d){}
bool operator < (const Line &b)const{
return h < b.h;
}
}LineX[MAXN*2],LineY[MAXN*2];
int X[MAXN*2];
int Y[MAXN*2];
struct D{
int value,cnt;
bool lazy;
}Tree[MAXN*4];
void Build(int temp,int left,int right){
Tree[temp].value = Tree[temp].cnt = 0;
Tree[temp].lazy = false;
if(left == right)return ;
int mid = left + (right-left)/2;
Build(temp<<1,left,mid);
Build(temp<<1|1,mid+1,right);
}
void Up(int temp){
if(Tree[temp<<1].cnt == -1 || Tree[temp<<1|1].cnt == -1)Tree[temp].cnt = -1;
else if(Tree[temp<<1].cnt != Tree[temp<<1|1].cnt)Tree[temp].cnt = -1;
else Tree[temp].cnt = Tree[temp<<1].cnt;
Tree[temp].value = Tree[temp<<1].value + Tree[temp<<1|1].value;
}
void PushDown(int temp,int left,int right,int T[]){
if(Tree[temp].lazy){
Tree[temp<<1].cnt = Tree[temp<<1|1].cnt = Tree[temp].cnt;
Tree[temp<<1].lazy = Tree[temp<<1|1].lazy = true;
if(Tree[temp].cnt>0){
int mid = left + (right-left)/2;
Tree[temp<<1].value = T[mid+1]-T[left];
Tree[temp<<1|1].value = T[right+1]-T[mid+1];
}
else Tree[temp<<1].value = Tree[temp<<1|1].value = 0;
Tree[temp].lazy = false;
}
}
void Updata(int temp,int left,int right,int ql,int qr,int flag,int T[]){
if(ql>right || qr<left)return;
if(ql<=left && qr>=right && Tree[temp].cnt!=-1){
Tree[temp].cnt += flag;
Tree[temp].lazy = true;
if(Tree[temp].cnt>0)Tree[temp].value = T[right+1]-T[left];
else Tree[temp].value = 0;
return ;
}
PushDown(temp,left,right,T);
int mid = left + (right-left)/2;
if(ql<=mid)Updata(temp<<1,left,mid,ql,qr,flag,T);
if(qr>mid)Updata(temp<<1|1,mid+1,right,ql,qr,flag,T);
Up(temp);
}
int Bin(int key,int right,int T[]){
int left,mid;
left = 0;
while(left<=right){
mid = left + (right-left)/2;
if(T[mid] == key)return mid;
else if(T[mid]>key)right = mid-1;
else left = mid+1;
}
return -1;
}
int main(){
int N;
int x1,x2,y1,y2;
long long sum;
while(scanf("%d",&N)!=EOF){
if(N==0){
printf("0\n");
continue;
}
int m = 0, n = 0;
sum = 0;
for(int i=0 ; i<N ; i++){
scanf("%d %d %d %d",&x1,&y1,&x2,&y2);
LineX[++n] = Line(y1,y2,x1,1);
Y[++m] = y1;
LineY[n] = Line(x1,x2,y1,1);
X[m] = x1;
LineX[++n] = Line(y1,y2,x2,-1);
Y[++m] = y2;
LineY[n] = Line(x1,x2,y2,-1);
X[m] = x2;
}
sort(X+1,X+m+1);
sort(Y+1,Y+m+1);
sort(LineX+1,LineX+1+n);
sort(LineY+1,LineY+1+n);
int t1 = unique(X+1,X+m+1)-X-1;
int t2 = unique(Y+1,Y+m+1)-Y-1;
Build(1,1,t1-1);
int last = 0,now = 0;
for(int i=1 ; i<=n ; i++){
int left = Bin(LineY[i].l,t1,X);
int right = Bin(LineY[i].r,t1,X)-1;
Updata(1,1,t1-1,left,right,LineY[i].v,X);
now = Tree[1].value;
sum += abs(now-last);
last = now;
}
Build(1,1,t2-1);
last = now = 0;
for(int i=1 ; i<=n ; i++){
int left = Bin(LineX[i].l,t2,Y);
int right = Bin(LineX[i].r,t2,Y)-1;
Updata(1,1,t2-1,left,right,LineX[i].v,Y);
now = Tree[1].value;
sum += abs(now-last);
last = now;
}
printf("%lld\n",sum);
}
return 0;
} 方法二：
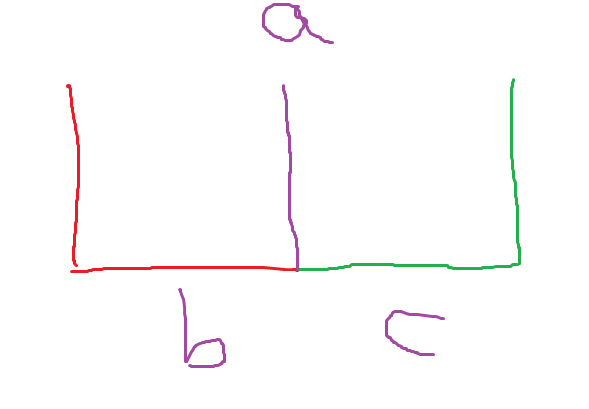
从左往右在每一次插入一条边后，周长并的累加值=新增的横边+新增的竖边。做过面积并题的人应该都知道如果只扫描一个方向的话写起来很简单，那么其实我们可以从下向上扫描一次，与方法一一样通过绝对值之差来求得新增的横边的长，而新增的竖边可以通过计算当前有几条横边来求。假如num条横线就能向上跳num*h*2（因为一条竖线两个端点）长度的竖线。因为我们在Up（返回子区间的值来更新父区间）时横线的数量可能会出现重复，如图：
图中b,c更新到a后其实只有一条横线。
所以为了解决这个问题我们需要用到线段树区间合并问题中的技巧，每个树节点再多加两个值表示区间的左右端点是否被覆盖。
代码：
ps：这种方法编译器用g++或c++都行，还快，所以如果能理解的话更推荐这一种。
#include <cstdio>
#include <algorithm>
using namespace std;
const int MAXN = 5005;
struct Line{
int l,r,h,flag;
Line(){}
Line(int a,int b,int c,int d):l(a),r(b),h(c),flag(d){}
bool operator < (const struct Line &e)const{
return h < e.h;
}
}L[MAXN*2];
struct T{
int value,len,flag,num;
bool rflag,lflag;//表示区间的左右端点是否被覆盖
bool lazy;
}Tree[MAXN*8];
int X[MAXN*2];
int Bin(int key,int right){
int left = 1,mid;
while(left <= right){
mid = left + (right-left)/2;
if(X[mid] == key)return mid;
else if(X[mid] > key)right = mid-1;
else left = mid+1;
}
return -1;
}
void Build(int temp,int left,int right){
Tree[temp].flag = Tree[temp].value = Tree[temp].num = 0;
Tree[temp].lazy = Tree[temp].lflag = Tree[temp].rflag = false;
Tree[temp].len = X[right+1]-X[left];
if(left == right)return ;
int mid = left + (right-left)/2;
Build(temp<<1,left,mid);
Build(temp<<1|1,mid+1,right);
}
void Up(int temp){
if(Tree[temp<<1].flag == -1 || Tree[temp<<1|1].flag == -1)Tree[temp].flag = -1;
else if(Tree[temp<<1].flag != Tree[temp<<1|1].flag)Tree[temp].flag = -1;
else Tree[temp].flag = Tree[temp<<1|1].flag;
Tree[temp].lflag = Tree[temp<<1].lflag;
Tree[temp].rflag = Tree[temp<<1|1].rflag;
Tree[temp].value = Tree[temp<<1].value + Tree[temp<<1|1].value;
Tree[temp].num = Tree[temp<<1].num + Tree[temp<<1|1].num - (Tree[temp<<1].rflag && Tree[temp<<1|1].lflag);
}
void PushDown(int temp){
if(Tree[temp].lazy){
Tree[temp<<1].lazy = Tree[temp<<1|1].lazy = true;
Tree[temp].lazy = false;
Tree[temp<<1].flag = Tree[temp<<1|1].flag = Tree[temp].flag;
if(Tree[temp].flag>0){
Tree[temp<<1].value = Tree[temp<<1].len;
Tree[temp<<1|1].value = Tree[temp<<1|1].len;
Tree[temp<<1].num = Tree[temp<<1|1].num = 1;
Tree[temp<<1].lflag = Tree[temp<<1].rflag = true;
Tree[temp<<1|1].lflag = Tree[temp<<1|1].rflag = true;
}
else {
Tree[temp<<1].value = Tree[temp<<1|1].value = 0;
Tree[temp<<1].num = Tree[temp<<1|1].num = 0;
Tree[temp<<1].lflag = Tree[temp<<1].rflag = false;
Tree[temp<<1|1].lflag = Tree[temp<<1|1].rflag = false;
}
}
}
void Updata(int temp,int left,int right,int ql,int qr,int flag){
if(ql>right || qr<left)return;
if(ql<=left && qr>=right && Tree[temp].flag!=-1){
Tree[temp].lazy = true;
Tree[temp].flag += flag;
if(Tree[temp].flag > 0){
Tree[temp].value = Tree[temp].len;
Tree[temp].num = 1;
Tree[temp].lflag = Tree[temp].rflag = true;
}
else Tree[temp].value = Tree[temp].num = Tree[temp].lflag = Tree[temp].rflag = false;
return;
}
PushDown(temp);
int mid = left + (right-left)/2;
if(ql<=mid)Updata(temp<<1,left,mid,ql,qr,flag);
if(qr>mid)Updata(temp<<1|1,mid+1,right,ql,qr,flag);
Up(temp);
}
int main(){
int N;
int x1,x2,y1,y2;
long long sum;
while(scanf("%d",&N)!=EOF){
if(N==0){
printf("0\n");
continue;
}
int m = 0, n = 0;
sum = 0;
for(int i=0 ; i<N ; i++){
scanf("%d %d %d %d",&x1,&y1,&x2,&y2);
L[++m] = Line(x1,x2,y1,1);
L[++m] = Line(x1,x2,y2,-1);
X[++n] = x1;
X[++n] = x2;
}
sort(X+1,X+n+1);
sort(L+1,L+1+m);
int t1 = unique(X+1,X+n+1)-X-1;
Build(1,1,t1-1);
int last = 0,now = 0;
L[m+1].h = L[m].h;
for(int i=1 ; i<=m ; i++){
int left = Bin(L[i].l,t1);
int right = Bin(L[i].r,t1)-1;
Updata(1,1,t1-1,left,right,L[i].flag);
now = Tree[1].value;
sum += abs(now-last);
sum += Tree[1].num*(L[i+1].h-L[i].h)*2;
last = now;
}
printf("%lld\n",sum);
}
return 0;
}
