2018 CCPC-Wannafly Camp #5 Problem F 平衡二叉树(打表找规律）

题目描述

平衡二叉树，顾名思义就是一棵“平衡”的二叉树。在这道题中，“平衡”的定义为，对于树中任意一个节点，都满足左右子树的高度差不超过 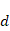. 空树的高度定义为0，单个节点的高度为1，其他情况下树的高度定义为根节点左右子树高度最大值 + 1。 一棵在高度上平衡的树，节点数可能不平衡。再定义一棵树的不平衡度为这棵树中所有节点的左右子树的节点数之差的最大值。

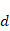
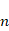
给定平衡的定义参数, 你需要求出所有高度为  的平衡树中不平衡度的最大值。

输入

两个整数，.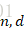

输出

一个整数：所有高度为 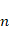 的平衡树中不平衡度的最大值。

样例输入

4 1

样例输出

5

提示

数据范围：
0 <= n, d <= 60

题解：

这道题应该是DP题，不过我DP极菜，只能使用最原始的办法——打表找规律。

首先我们固定让结果树的左子树节点数大于右子树，那么易知左子树的节点只需要按二叉树填满就可以达到最大，也就是

2^(N-1)-1个节点。那么要让结果最大只需要让右子树的节点数最少，随便写几个当D = 1，N为2,3,4....的数发现右子树最少节点数为0,1,2,4,7,12.......，容易发现从N=5开始，右子树最少节点数为前两个的和+1。由此就想着会不会有什么规律。

打表代码：

#include <cstdio>

using namespace std;

typedef struct Node* node;

int N,D;

struct Node{
	int num;
	node l,r;
	Node(){
		l = r = NULL;
		num = 1;
	}
};

int re;

int DFS(int t,node root){
	if(t <= 0)return 0;
	root->l = new Node();
	root->num += DFS(t-1,root->l);
	re++;
	if(root->num-1 > D){
		root->r = new Node();
		DFS(root->num-1-D,root->r);
	}
	return root->num;
}

long long Mypow(long long a,long long b){
	long long t = 1;
	while(b){
		if(b&1)t *= a;
		a *= a;
		b /= 2;
	}
	return t;
}

void Del(node root){
	if(!root)return;
	Del(root->l);
	Del(root->r);
	delete(root);
}

int main(){

	for(N=1 ; N<=20 ; ++N){ 
		printf("N %d:",N);
		re = 0;
		D = 1;//D在这手动修改 
		if(N < 2)printf("0\n");
		node root = new Node();
		int t = DFS(N-1-D,root);
		//long long tt = Mypow(2,N-1)-1;
		printf("---%lld\n",re);
		Del(root);
	}
	
	return 0;
}

打了D=1,2,3,4的表后果然发现个规律（太难描述，自己打表观察吧，很容易的。_(:з」∠)_）

最后AC代码：

#include <cstdio>
 
using namespace std;
 
long long board[100][100];
 
long long Mypow(long long a,long long b){
    long long t = 1;
    while(b){
        if(b&1)t *= a;
        a *= a;
        b /= 2;
    }
    return t;
}
 
int main(){
     
    for(int i=1 ; i<=60 ; ++i){
        for(int j=1 ; j<=i+1 ; ++j){
            board[i][j] = j;
        }
        for(int j=i+2 ; j<=60 ; ++j){
            board[i][j] = board[i][j-1] + board[i][j-1-i] + 1; 
        }
    }
    int N,D;
    while(scanf("%d %d",&N,&D) == 2){
        if(N < 2 || D == 0){
            printf("0\n");
            continue;
        }
        long long t = Mypow(2,N-1)-1;
        printf("%lld\n",t-board[D][N-1-D]);
    }
     
    return 0;
}
/**************************************************************
    Problem: 1087
    User: 2016203524
    Language: C++
    Result: 正确
    Time:0 ms
    Memory:1036 kb
****************************************************************/