摘要: 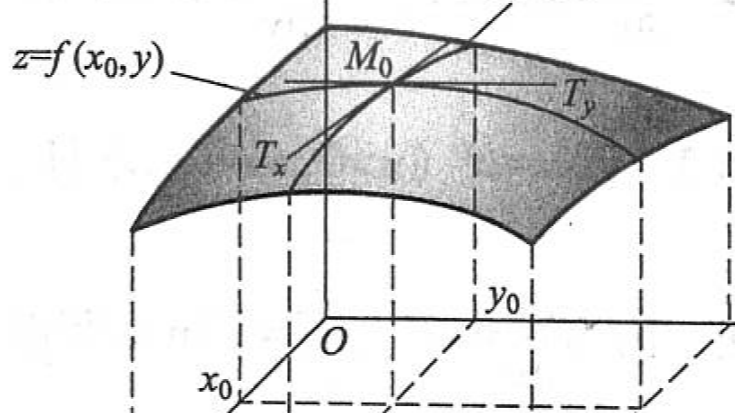 目录一、偏导数的定义及其计算法二、高阶偏导数 一、偏导数的定义及其计算法 定义 设函数 \(z=f(x, y)\) 在点 \(\left(x_{0}, y_{0}\right)\) 的某一邻域内有定义,当 \(y\) 固定在 \(y_{0}\) 而 \(x\) 在 \(x_{0}\) 处有增量 \( 阅读全文
目录一、偏导数的定义及其计算法二、高阶偏导数 一、偏导数的定义及其计算法 定义 设函数 \(z=f(x, y)\) 在点 \(\left(x_{0}, y_{0}\right)\) 的某一邻域内有定义,当 \(y\) 固定在 \(y_{0}\) 而 \(x\) 在 \(x_{0}\) 处有增量 \( 阅读全文
 目录一、偏导数的定义及其计算法二、高阶偏导数 一、偏导数的定义及其计算法 定义 设函数 \(z=f(x, y)\) 在点 \(\left(x_{0}, y_{0}\right)\) 的某一邻域内有定义,当 \(y\) 固定在 \(y_{0}\) 而 \(x\) 在 \(x_{0}\) 处有增量 \( 阅读全文
目录一、偏导数的定义及其计算法二、高阶偏导数 一、偏导数的定义及其计算法 定义 设函数 \(z=f(x, y)\) 在点 \(\left(x_{0}, y_{0}\right)\) 的某一邻域内有定义,当 \(y\) 固定在 \(y_{0}\) 而 \(x\) 在 \(x_{0}\) 处有增量 \( 阅读全文
posted @ 2025-08-25 19:56
暮颜
阅读(280)
评论(0)
推荐(0)

 目录一、空间曲线的一般方程二、空间曲线的参数方程*曲面的参数方程三、空间曲线在坐标平面上的投影 一、空间曲线的一般方程 我们已经知道空间曲线可以看做两个曲面的交线。设 \[F(x, y, z) = 0 \quad 和 \quad G(x, y, z) = 0 \]是两个曲面的方程,则方程组 \[\b
目录一、空间曲线的一般方程二、空间曲线的参数方程*曲面的参数方程三、空间曲线在坐标平面上的投影 一、空间曲线的一般方程 我们已经知道空间曲线可以看做两个曲面的交线。设 \[F(x, y, z) = 0 \quad 和 \quad G(x, y, z) = 0 \]是两个曲面的方程,则方程组 \[\b  在空间解析几何中,关于曲面的研究有下列两个基本问题:
(1)已知一曲面作为点的几何轨迹时,建立这曲面的方程;
(2)已知坐标 $x, y, z$ 间的一个方程时,研究这方程所表示的曲面的形状。
在空间解析几何中,关于曲面的研究有下列两个基本问题:
(1)已知一曲面作为点的几何轨迹时,建立这曲面的方程;
(2)已知坐标 $x, y, z$ 间的一个方程时,研究这方程所表示的曲面的形状。  浙公网安备 33010602011771号
浙公网安备 33010602011771号