Codeforces Round #686 (Div. 3)E题求简单路径的个数

Codeforces Round #686 (Div. 3) E题求简单路径的个数

大意：给一个n个节点n条边的无向图，求简单路径的个数。

思路：先拓扑排序，我们从度为1的叶节点开始，把除环上的节点全部标记成已访问（环上的节点的度>=2，不会变成1），然后依次从环上的每一点，dfs它的子树，得到每一部分子树的节点数。

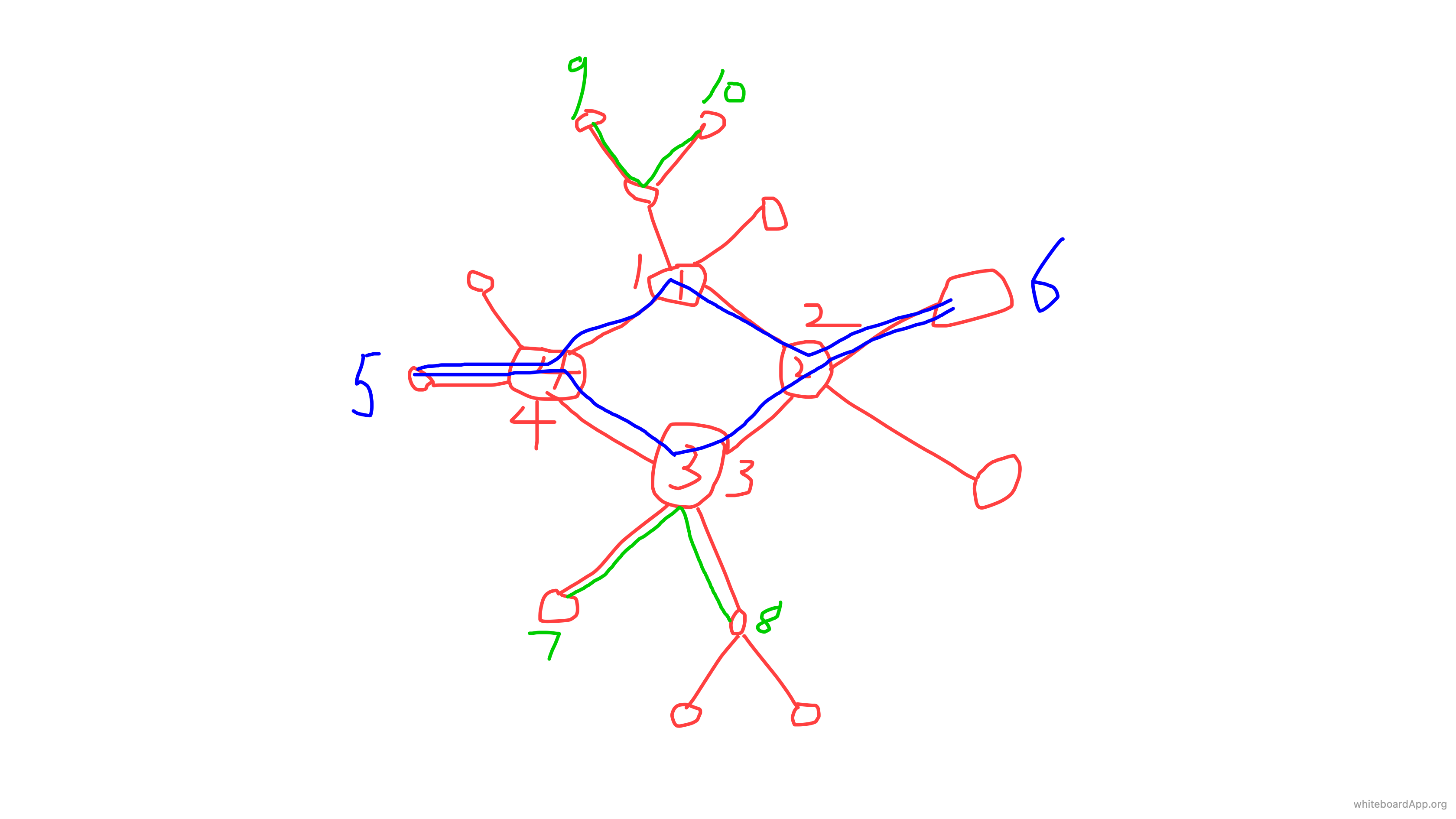
如图，1，2，3，4是环上的点，共有4棵树。简单路径个数如下：

• 简单路径不通过环上的边：两个节点在同一棵树内，树的节点数为m，那么就是m * (m - 1) / 2。（图中绿色的路径，9、10两个点之间有一条路径）
• 简单路径通过环上的边：两个节点在不同的树内，树的节点数为m1、m2，那么就是m1 * m2。（图中蓝色的路径，5、6两个点之间有两条路径）

但我们不需要这么麻烦去计算每个树的节点个数。只需要计算n * (n - 1)，这个结果多计算了第一种情况，就是两个节点在同一棵树内，我们只需要减去每棵树的内部路径个数就行了。

代码

#include <iostream>
#include <vector>
#include <queue>

using namespace std;

long long dfs(int v, int father, vector<vector<int>>& g, vector<int>& vis)
{
    long long nodes = 1;
    for(int u : g[v])
    {
        if(u == father || !vis[u]) continue;	// 判断father是去掉自环的情况。
        nodes += dfs(u, v, g, vis);
    }
    return nodes;
}

int main()
{
    cin.tie(nullptr);
    int t, n;
    cin >> t;
    while(t--)
    {
        cin >> n;
        vector<vector<int>> g(n, vector<int>());
        vector<int> vis(n, 0);
        vector<int> deg(n, 0);
        // read edges
        for(int i = 0; i < n; i++)
        {
            int x, y;
            cin >> x >> y;
            x--, y--;
            g[x].push_back(y);
            g[y].push_back(x);
            deg[x]++;
            deg[y]++;
        }
        // topsort
        queue<int> Q;
        for(int i = 0; i < n; i++)
            if(deg[i] == 1) Q.push(i);	// 从叶子节点开始，他们的度都为1。
        long long noCycles = 0;
        while(!Q.empty())
        {
            int v = Q.front(); Q.pop();
            vis[v] = 1;
            noCycles++;
            for(int u : g[v])
            {
                deg[u]--;
                if(deg[u] == 1) Q.push(u);
            }
        }
        // 到这里所有非环上节点已被标记成vis，环上的节点的度是 >= 2 的，所以不会被标记
        long long res = n * (n - 1);
        for(int i = 0; i < n; i++)
        {		// 环上节点，去计算以它为根的树的节点个数
            if(!vis[i])
            {
                long long treeI = dfs(i, i, g, vis);
                res -= (treeI) * (treeI - 1) / 2;
            }
        }
        cout << res << "\n";
    }
}