Ceres学习-1.CostFunction

CostFunction的概念参考 https://www.cnblogs.com/vivian187/p/15398068.html

Ceres求解器，像所有基于梯度的优化算法一样，依赖于能够评估目标函数及其在其域内任意点的导数。实际上，定义目标函数及其雅可比矩阵是用户在使用Ceres求解器求解优化问题时需要执行的主要任务。正确、高效的雅可比矩阵计算是获得良好性能的关键

非线性优化涉及到对目标函数进行求导，从而迭代优化。

Ceres Solver提供了三种求导方式：

• 自动求导: 自动求导是通过定义一个仿函数，然后传给AutoDiffCostFunction/...，就可以让Ceres自己去求导。

• 数值求导: 有时，无法定义自动求导的模板仿函数，比如参数的估计调用了无法控制的库函数或外部函数。这种情况无法使用自动求导了，数值求导便可以派上用场了。
           数值求导用法类似，先定义仿函数，然后传递给NumericDiffCostFunction/...，然后去构造问题求解。

• 解析求导: 有些情况，自己写求导解析式，计算效率会更高一些。
           如果使用解析求导的方式，就要自行计算残差和雅克比。

1.自动求导

1.1 定义仿函数

仿函数，其实是一个类，只不过这个类的作用像函数，所以叫仿函数。原理就是类实现了operator()函数。
仿函数参考: https://www.cnblogs.com/vivian187/p/15329482.html

// 来自ceres-solver-1.14.0/examples/helloworld.cc
struct CostFunctor {
  template <typename T> bool operator()(const T* const x, T* residual) const {
    residual[0] = 10.0 - x[0];
    return true;
  }
};

要获得自动求导代价函数，必须定义一个带有模板化operator()(仿函数)的类，该操作符根据模板形参T计算代价函数。
operator()函数必须在最后一个实参(唯一的非const实参，即残差)中写入计算值，并返回true表示成功。

1.2 构造代价函数

// 来自ceres-solver-1.14.0/examples/helloworld.cc
CostFunction* cost_function = new AutoDiffCostFunction<CostFunctor, 1, 1>(new CostFunctor);

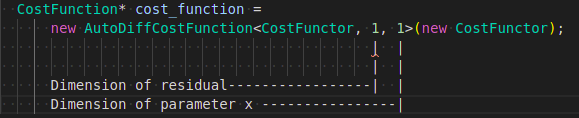
AutoDiffCostFunction的模板参数说明：

第1个模板参数是仿函数CostFunctor
第2个模板参数是残差块中残差的数量
第3个模板参数是第一个参数块中参数的数量
如果有多个参数块，则第4/5...个模板参数: 依次写出各个参数块中参数的数量

1.3 Ceres提供的类

Ceres提供的自动求导仿函数：

AutoDiffCostFunction类（上面的例子）
DynamicAutoDiffCostFunction类

参考：
https://www.cnblogs.com/vivian187/p/15349110.html#3autodiffcostfunction

2.数值求导

2.1 定义仿函数

// 来自ceres-solver-1.14.0/examples/helloworld_numeric_diff.cc
struct CostFunctor {
  bool operator()(const double* const x, double* residual) const {
    residual[0] = 10.0 - x[0];
    return true;
  }
};

与自动求导的仿函数不同的是，数值求导的operator()函数不是模板函数，而是直接使用了double

2.2 构造代价函数

// 来自ceres-solver-1.14.0/examples/helloworld_numeric_diff.cc
  CostFunction* cost_function =
      new NumericDiffCostFunction<CostFunctor, CENTRAL, 1, 1> (new CostFunctor);

和自动求导方法相比，在用数值求导时需要额外给定一个参数ceres::CENTRAL 。这个参数告诉计算机如何计算导数。

NumericDiffCostFunction的模板参数说明：

第1个模板参数是仿函数CostFunctor
第2个模板参数是数值求导的方式。这里选用了CENTRAL，还有FORWARD、RIDDERS等
第3个模板参数是残差块中残差的数量
第4个模板参数是第一个参数块中参数的数量
如果有多个参数块，则第4/5...个模板参数: 依次写出各个参数块中参数的数量

2.3 Ceres提供的类

Ceres提供的数值求导仿函数：

NumericDiffCostFunction类（上面的例子）
DynamicNumericDiffCostFunction类

参考：
https://www.cnblogs.com/vivian187/p/15349110.html#3autodiffcostfunction

3.解析求导

3.1 定义代价函数类

// 来自ceres-solver-1.14.0/examples/helloworld_analytic_diff.cc
// A CostFunction implementing analytically derivatives for the
// function f(x) = 10 - x.
class QuadraticCostFunction
  : public SizedCostFunction<1 /* number of residuals */,
                             1 /* size of first parameter */> {
 public:
  virtual ~QuadraticCostFunction() {}

  virtual bool Evaluate(double const* const* parameters,
                        double* residuals,
                        double** jacobians) const {
    double x = parameters[0][0];

    // f(x) = 10 - x.
    residuals[0] = 10 - x;

    // f'(x) = -1. Since there's only 1 parameter and that parameter
    // has 1 dimension, there is only 1 element to fill in the
    // jacobians.
    //
    // Since the Evaluate function can be called with the jacobians
    // pointer equal to NULL, the Evaluate function must check to see
    // if jacobians need to be computed.
    //
    // For this simple problem it is overkill to check if jacobians[0]
    // is NULL, but in general when writing more complex
    // CostFunctions, it is possible that Ceres may only demand the
    // derivatives w.r.t. a subset of the parameter blocks.
    if (jacobians != NULL && jacobians[0] != NULL) {
      jacobians[0][0] = -1;
    }

    return true;
  }
};

自定义的代价函数类要继承自CostFunction或者SizedCostFunction。其实SizedCostFunction是继承自CostFunction的，只是确定了size(各个参数块的数量)。
Evaluate()函数中计算了残差和雅克比。

3.2 构造代价函数

// 来自ceres-solver-1.14.0/examples/helloworld_analytic_diff.cc
CostFunction* cost_function = new QuadraticCostFunction;

3.3 Ceres提供的类

Ceres提供的解析求导代价函数类：

CostFunction类
SizedCostFunction类（上面的例子）

参考：
https://www.cnblogs.com/vivian187/p/15349110.html#3autodiffcostfunction

3.4 什么情况下使用解析求导

按照官方说明，以下情况可以使用解析求导

函数式简单，便于求出导数解析式
能使用Matlab Maple Mathmatic SymPy等数学软件求出了导数的解析式
性能极致要求
没有其他好的方法去求导
喜欢手算导数

综上所述，建议优先使用自动求导和数值求导的方式，对雅克比计算擅长者和极致性能追求者可考虑使用解析求导的方式。

参考
https://www.jianshu.com/p/39d8e0f31bbf
https://blog.csdn.net/ktigerhero3/article/details/85062092