17.Ceres官方教程-Modeling Non-linear Least Squares (5) LocalParameterization
1.LocalParameterization
在许多优化问题中，特别是传感器融合问题中，我们必须对流形空间中的数量进行建模，例如由四元数表示的传感器的旋转/方向。
流形是空间，其局部看起来像欧几里得空间。更准确地说，在流形上的每一点上，都有一个与流形相切的线性空间。它的维数等于流形本身的内在维数，而内在维数小于或等于流形所嵌入的环境空间。
例如，在三维空间中，球面上一点的切空间就是二维平面，在这一点上与球面相切。切线空间之所以有趣有两个原因:
- 它们是欧几里得空间，所以通常的向量空间运算适用于这里，这使得数值运算很容易。
- 切线空间中的运动转化为沿流形的运动。垂直于切线空间的运动不会转化为流形上的运动。
Returning to our sphere example, moving in the 2 dimensional plane tangent to the sphere and projecting back onto the sphere will move you away from the point you started from but moving
along the normal at the same point and the projecting back onto the sphere brings you back to the point.
除了数学上的精细，正确地建模流形数值并注意其几何形状也有实际的好处:
- 通过优化，它自然地将数量约束在流形上。将用户从四元数规范化中解放出来。
- 它将优化问题的维数降低到其natural size。例如，一个限制在一条线上的量，是一个一维的物体，与这条线所在的环境空间的维度无关。
在切线空间中工作不仅降低了优化算法的计算复杂度，而且还改善了算法的数值行为。
在流形上可以执行的一个基本操作是
操作，它计算在x处沿切空间移动的结果，然后投影回x所属的流形上。
是欧几里得空间中向量加法的一种推广。形式上，是从一个流形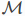
及其切空间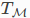
到服从恒等式的流形
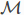的光滑映射。
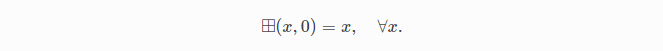
That is, it ensures that the tangent space is centered at and the zero vector is the identity element.
让我们考虑两个例子:
欧几里得空间
是流形的最简单的例子。
它的维数是n(它的切空间也是)，
是我们熟悉的向量和运算。
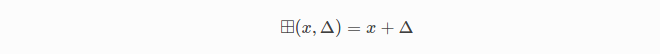
一个更有趣的例子是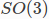
，它是三维空间中特殊的正交群——3 × 3旋转矩阵的空间。
是嵌入在
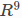或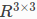
中的三维流形。
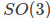上的
是用指数映射定义的，从切空间(
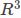)到流形。指数映射定义为:
class LocalParameterization {
public:
virtual ~LocalParameterization() {}
virtual bool Plus(const double* x,
const double* delta,
double* x_plus_delta) const = 0;
virtual bool ComputeJacobian(const double* x, double* jacobian) const = 0;
virtual bool MultiplyByJacobian(const double* x,
const int num_rows,
const double* global_matrix,
double* local_matrix) const;
virtual int GlobalSize() const = 0;
virtual int LocalSize() const = 0;
};
参数块x所在的环境空间的维数。
所在的切线空间的大小。
LocalParameterization::Plus()实现了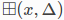
。
计算雅可比矩阵
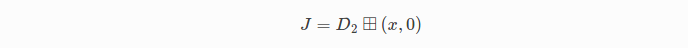
in row major form.
local_matrix = global_matrix * jacobian
global_matrix是一个num_rows x GlobalSize行主矩阵。local_matrix是一个num_rows x LocalSize行主矩阵。jacobian是LocalParameterization::ComputeJacobian()在x处返回的矩阵。
这只在GradientProblem中使用。对于大多数正常使用，使用默认实现是可以的。
Ceres求解器附带了一些常用的LocalParameterization实例。在各种流形上找到
运算的高质量实现的另一个好地方是Hauke Strasdat和他的合作者开发的Sophus库。
IdentityParameterization
TODO...
QuaternionParameterization
TODO...
EigenQuaternionParameterization
TODO...
SubsetParameterization
TODO...
HomogeneousVectorParameterization
TODO...
LineParameterization
TODO...
ProductParameterization
TODO...
2.AutoDiffLocalParameterization
AutoDiffLocalParameterization相对于LocalParameterization做的事就像AutoDiffCostFunction相对于CostFunction的一样。
它允许用户定义一个模板化的仿函数来实现LocalParameterization::Plus()操作，并使用自动微分来实现雅可比矩阵的计算。
要获得自动微分的局部参数化，必须定义一个具有模板化operator()(仿函数)的类来进行计算。
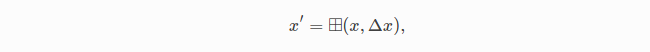
例如，四元数具有三维局部参数化。它的加操作可以实现为(来自于internal/ceres/autodiff_local_parameterization_test.cc)
struct QuaternionPlus {
template<typename T>
bool operator()(const T* x, const T* delta, T* x_plus_delta) const {
const T squared_norm_delta =
delta[0] * delta[0] + delta[1] * delta[1] + delta[2] * delta[2];
T q_delta[4];
if (squared_norm_delta > 0.0) {
T norm_delta = sqrt(squared_norm_delta);
const T sin_delta_by_delta = sin(norm_delta) / norm_delta;
q_delta[0] = cos(norm_delta);
q_delta[1] = sin_delta_by_delta * delta[0];
q_delta[2] = sin_delta_by_delta * delta[1];
q_delta[3] = sin_delta_by_delta * delta[2];
} else {
// We do not just use q_delta = [1,0,0,0] here because that is a
// constant and when used for automatic differentiation will
// lead to a zero derivative. Instead we take a first order
// approximation and evaluate it at zero.
q_delta[0] = T(1.0);
q_delta[1] = delta[0];
q_delta[2] = delta[1];
q_delta[3] = delta[2];
}
Quaternionproduct(q_delta, x, x_plus_delta);
return true;
}
};
对于这个结构，自动微分局部参数化现在可以构造为
