15.Ceres官方教程-Modeling Non-linear Least Squares (3)

目录

• 1.GradientChecker
• 2.NormalPrior

1.GradientChecker

这个类比较由代价函数返回的雅可比矩阵与用有限微分估计的导数。它是一种用于单元测试的工具，比求解器选项中的check_gradients选项提供更fine-grained的控制。

强制执行的条件是

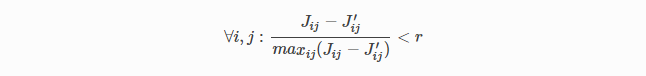
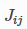由用户提供的成本函数乘以局部参数雅可比矩阵计算出来的雅可比矩阵, 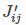是由有限微分乘以局部参数雅可比矩阵，计算出来的雅可比矩阵。r是相对精度。
用法:

//  my_cost_function takes two parameter blocks. The first has a local
//  parameterization associated with it.
CostFunction* my_cost_function = ...
LocalParameterization* my_parameterization = ...
NumericDiffOptions numeric_diff_options;

std::vector<LocalParameterization*> local_parameterizations;
local_parameterizations.push_back(my_parameterization);
local_parameterizations.push_back(nullptr);

std::vector parameter1;
std::vector parameter2;
// Fill parameter 1 & 2 with test data...

std::vector<double*> parameter_blocks;
parameter_blocks.push_back(parameter1.data());
parameter_blocks.push_back(parameter2.data());

GradientChecker gradient_checker(my_cost_function,
    local_parameterizations, numeric_diff_options);
GradientCheckResults results;
if (!gradient_checker.Probe(parameter_blocks.data(), 1e-9, &results) {
  LOG(ERROR) << "An error has occurred:\n" << results.error_log;
}

2.NormalPrior

class NormalPrior: public CostFunction {
 public:
  // Check that the number of rows in the vector b are the same as the
  // number of columns in the matrix A, crash otherwise.
  NormalPrior(const Matrix& A, const Vector& b);

  virtual bool Evaluate(double const* const* parameters,
                        double* residuals,
                        double** jacobians) const;
 };

实现公式的代价函数

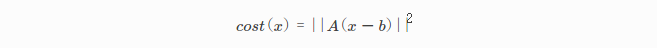
矩阵A和向量b是常量，x是变量。如果用户对实现公式的代价函数感兴趣。

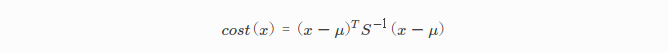
式中，μ是向量，S是协方差矩阵，则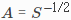，即矩阵A是协方差逆的平方根，也称为刚度矩阵。

但是对A的形状没有限制，它可以是矩形的，如果协方差矩阵S缺秩，就可以是矩形。