14.Ceres官方教程-Modeling Non-linear Least Squares (2) 多种CostFunction

目录

1.CostFunction

对于目标函数中的每一项，CostFunction负责计算残差向量和雅可比矩阵。具体地，考虑一个依赖于参数块的函数。

然后，对于一个给定的，CostFunction负责计算向量和雅克比矩阵

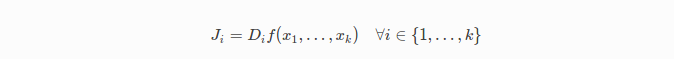
class CostFunction {
 public:
  virtual bool Evaluate(double const* const* parameters,
                        double* residuals,
                        double** jacobians) = 0;
  const vector<int32>& parameter_block_sizes();
  int num_residuals() const;

 protected:
  vector<int32>* mutable_parameter_block_sizes();
  void set_num_residuals(int num_residuals);
};
// PS:这只是CostFunction类的主要成员，代码在ceres-solver-1.14.0(或其他版本)/include/ceres/cost_function.h中

CostFunction类输入参数块的数量和大小被记录在CostFunction::parameter_block_sizes_，输出残差的个数被记录在CostFunction::num_residuals_。
从这个类继承的用户代码应该使用相应的访问器设置这两个成员。当添加到Problem::AddResidualBlock()时，该信息将由Problem验证。

功能：计算残差向量和雅可比矩阵。

  • parameters: parameters是一个大小为CostFunction::parameter_block_sizes_.size()的数组，parameters[i]是一个大小为parameter_block_sizes_[i]的数组，其中包含CostFunction所依赖的第i个参数块。parameters不会为nullptr。
  • residuals: 是一个大小为num_residuals_的数组。residuals也不会为nullptr。
  • jacobians: 是一个大小为CostFunction::parameter_block_sizes_.size()的数组。
    1. 如果jacobians是nullptr，用户只需要计算残差。
  • jacobians[i]: 是一个大小为 num_residuals x parameter_block_sizes_[i] 的行数组
    1. 如果jacobians[i]不为nullptr，用户需要计算关于parameters[i]的残差向量的雅可比矩阵，并将其存储在这个数组中，即
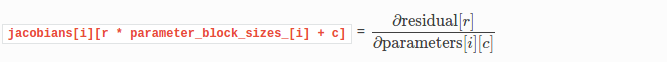
    2. 如果jacobians[i]是nullptr，然后可以跳过这个计算。这是当相应的参数块被标记为常量时的情况。

返回值表明残差和/或雅可比矩阵的计算是否成功。例如，这可以用于传达雅可比矩阵计算中的数值失败。

2.SizedCostFunction


如果在编译时知道参数块的大小和残差向量的大小(这是常见的情况)，则可以使用SizedCostFunction，这些值可以被指定为模板参数，用户只需要实现CostFunction::Evaluate()。

template<int kNumResiduals, int... Ns>
class SizedCostFunction : public CostFunction {
 public:
  virtual bool Evaluate(double const* const* parameters,
                        double* residuals,
                        double** jacobians) const = 0;
};

3.AutoDiffCostFunction


定义一个CostFunction或SizedCostFunction是一件乏味且容易出错的事情，尤其是在计算导数时。为此，Ceres提供了自动差分。

template <typename CostFunctor,
       int kNumResiduals,  // Number of residuals, or ceres::DYNAMIC.
       int... Ns>          // Size of each parameter block
class AutoDiffCostFunction : public
SizedCostFunction<kNumResiduals, Ns> {
 public:
  AutoDiffCostFunction(CostFunctor* functor, ownership = TAKE_OWNERSHIP);
  // Ignore the template parameter kNumResiduals and use
  // num_residuals instead.
  AutoDiffCostFunction(CostFunctor* functor,
                       int num_residuals,
                       ownership = TAKE_OWNERSHIP);
};

要获得自动微分代价函数(cost function)，必须定义一个带有模板化operator()(仿函数)的类，该操作符根据模板形参T计算代价函数。
自动微分框架将适当的用Jet对象替换为T，以便在必要时计算导数，但这是隐藏的，您应该将函数写成T是一个标量类型(例如，一个双精度浮点数)。
operator()函数必须在最后一个实参(唯一的非const实参，即残差)中写入计算值，并返回true表示成功。

例如，考虑一个标量误差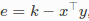，其中x和y都是二维矢量参数，k是常数。
这种误差的形式，即常数和表达式之间的差异，是最小二乘问题中的一种常见模式。例如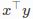，值可能是一系列测量的模型期望值，每一次测量k都对应了一个代价函数类的实例。

实际代价函数添加到problem中是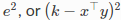，然而，平方是由优化框架隐式完成的。
要为上述模型编写一个自动可微分的成本函数，首先定义对象

class MyScalarCostFunctor {
  MyScalarCostFunctor(double k): k_(k) {}

  template <typename T>
  bool operator()(const T* const x , const T* const y, T* e) const {
    e[0] = k_ - x[0] * y[0] - x[1] * y[1];
    return true;
  }

 private:
  double k_;
};

注意，在operator()的声明中，输入形参x和y在前面，并作为指向数组T的const指针传递。如果有三个输入参数，那么第三个输入参数将出现在y后面。
输出总是最后一个参数，也是一个指向数组的指针。在上面的例子中，e是一个标量，所以只有e[0]被设置。

给出该类定义，可构造其自动微分代价函数:

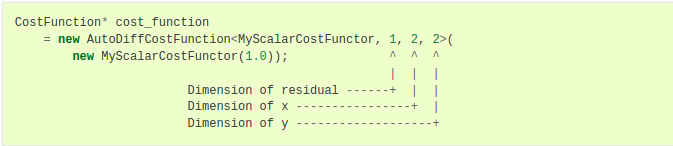
在这个例子中，通常对于k的每一个测量值都有一个实例。

在上面的实例化中，MyScalarCostFunction后面的模板参数， < 1,2,2 >将仿函数描述为从两个二维参数计算一维输出。

默认情况下AutoDiffCostFunction将获得传递给它的代价函数指针的所有权。当AutoDiffCostFunction本身被删除时，将对代价函式函数调用delete。然而，在某些情况下这可能是不可取的，
因此也可以在构造函数中指定DO_NOT_TAKE_OWNERSHIP作为第二个参数，同时传递一个不需要被AutoDiffCostFunction删除的cost functor指针。例如:

MyScalarCostFunctor functor(1.0)
CostFunction* cost_function
    = new AutoDiffCostFunction<MyScalarCostFunctor, 1, 2, 2>(
        &functor, DO_NOT_TAKE_OWNERSHIP);

AutoDiffCostFunction还支持具有运行时才确定残差数量的代价函数。例如:

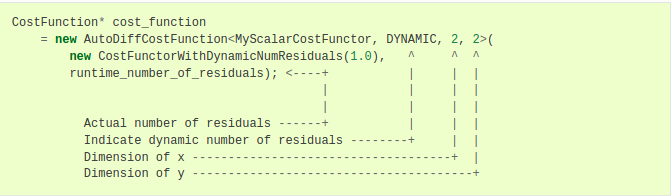
注意，新用户常常犯的一个错误就是把模板参数中的数字理解成参数的个数。但事实上，模板参数中数字的含义是每个参数的维度。这两个概念不能混淆。比如在这个例子中x y都是二维变量，所以模板参数中有两个2。

4.DynamicAutoDiffCostFunction


AutoDiffCostFunction要求在编译时知道参数块的数量和大小。在许多应用中，这是不够的，例如，贝塞尔曲线拟合，神经网络训练等。

template <typename CostFunctor, int Stride = 4>
class DynamicAutoDiffCostFunction : public CostFunction {
};

在这种情况下，可以使用DynamicAutoDiffCostFunction。与AutoDiffCostFunction一样，用户必须定义一个模板化的仿函数，但是仿函数的声明略有不同。cost functors的预期接口是:

struct MyCostFunctor {
  template<typename T>
  bool operator()(T const* const* parameters, T* residuals) const {
  }
}

由于参数的大小是在运行时完成的，因此还必须在创建DynamicAutoDiffCostFunction之后指定大小。例如:

DynamicAutoDiffCostFunction<MyCostFunctor, 4>* cost_function =
  new DynamicAutoDiffCostFunction<MyCostFunctor, 4>(
    new MyCostFunctor());
cost_function->AddParameterBlock(5);
cost_function->AddParameterBlock(10);
cost_function->SetNumResiduals(21);

在底层，对代价函数的计算分多次进行，每次计算一小组微分(默认情况下4个，由Stride模板参数控制)。分组更小计算更高效，但会导致更多次的运算。而更大分组虽然可以同时减少计算次数，但是有时候会造成缓存数据损失。必须对此做出权衡。最优值取决于各种参数块的数量和大小。建议在使用DynamicAutoDiffCostFunction之前，先试着用AutoDiffCostFunction。

5.NumericDiffCostFunction

在某些情况下，不能定义模板化的cost仿函数，例如，当残差的求值涉及调用您无法控制的库函数时。在这种情况下，可以使用数值微分法。

template <typename CostFunctor,
          NumericDiffMethodType method = CENTRAL,
          int kNumResiduals,  // Number of residuals, or ceres::DYNAMIC.
          int... Ns>          // Size of each parameter block.
class NumericDiffCostFunction : public
SizedCostFunction<kNumResiduals, Ns> {
};

要获得数值微分的CostFunction，必须定义一个带有operator()(仿函数)的类来计算残差。
仿函数必须在最后一个实参(唯一的非const实参，即残差)中写入计算值，并返回true以表示成功。
有关如何使用返回值对参数块施加简单约束的详细信息，请参阅CostFunction。例如，一个例子

struct ScalarFunctor {
 public:
  bool operator()(const double* const x1,
                  const double* const x2,
                  double* residuals) const;
}

例如，考虑一个标量误差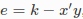，其中x和y都是二维列向量参数，’表示转置，k是常数。这种误差的形式，即常数和表达式之间的差异，是最小二乘问题中的一种常见模式。
例如，值x'y可能是一系列测量的模型期望值，其中每个测量k都有一个成本函数实例。
为上面的模型编写一个数值微分的类:CostFunction，首先定义对象

class MyScalarCostFunctor {
  MyScalarCostFunctor(double k): k_(k) {}

  bool operator()(const double* const x,
                  const double* const y,
                  double* residuals) const {
    residuals[0] = k_ - x[0] * y[0] + x[1] * y[1];
    return true;
  }

 private:
  double k_;
};

注意: 在operator()函数中，输入参数x，y在前面，作为常量指针double数组传递。如果有3个输入参数，第三个输入参数在参数y后面。输出是最后一个参数，并且也是一个数组的指针。
在上面的例子中，残差是一个标量，因此仅设置residuals[0]。

然后给出该类定义，可构造出用于计算导数的具有中心微分的数值微分CostFunction，如下图所示。

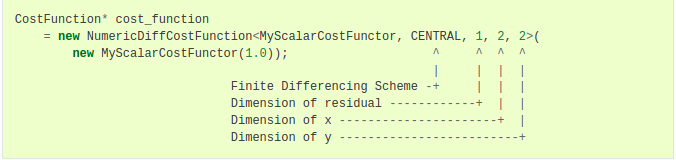
在这个例子中，通常对于每次测量k都有一个实例。

在上面的实例化中，MyScalarCostFunctor后面的模板参数, 1,2,2 将仿函数描述为从两个二维的参数计算一维输出。
NumericDiffCostFunction还支持在运行时才确定残差数量的成本函数。例如:

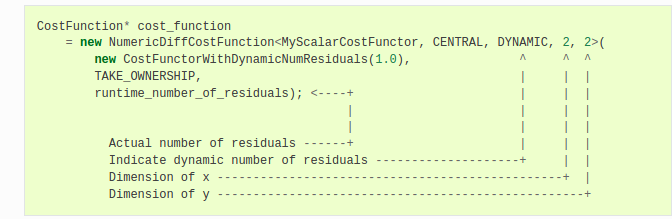
在ceres-solver中有三种可用的数值微分方案:

  • FORWARD微分方法: 通过计算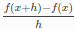近似估计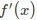，在x+h处额外计算一次代价函数。这是最快但不精确的方法。
  • CENTRAL微分方法: 更精确，但代价是前向微分的两倍，通过近似估计。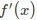
  • RIDDERS微分方法: 是一种自适应方案，通过在不同尺度(scales)上执行多个中心微分来估计导数。具体来说，算法从一个特定的h开始，随着导数的估计，步长减小。为了保持函数值和估计导数误差，该方法在测试步长之间进行Richardson extrapolations。该算法显示了相当高的精度，但通过额外的代价函数的评估来实现。

首先考虑使用CENTRAL微分。根据结果，要么尝试forward微分来提高性能，要么Ridders的方法来提高精度。

Numeric Differentiation & LocalParameterization

如果你的代价函数依赖于一个必须位于流形上的参数块，而仿函数不能计算不在流形上的参数块的值来计算，那么你可能会遇到数值微分这些仿函数的问题。

PS： 流形，也就是 Manifold。https://www.cnblogs.com/icmzn/p/11082509.html

这是因为Ceres中的数值微分是通过扰动代价仿函数所依赖的参数块的单个坐标来实现的。在此过程中，我们假设参数块存在于欧几里德空间中，而忽略了它们所处的流形结构。因此，一些扰动可能不在与参数块对应的流形上。

例如，考虑一个被解释为单位四元数的四维参数块。扰动这个参数块的坐标将违反参数块的单位范数属性。

解决这个问题需要NumericDiffCostFunction知道与每个参数块相关的LocalParameterization，并且只在每个参数块的局部切空间中生成扰动。

目前，这还不是一个严重到需要更改NumericDiffCostFunction API的问题。此外，在大多数情况下，在仿函数中使用流形之前，将流形上的一个点投影回流形是相对直接的。例如在四元数的情况下，在使用它之前对4向量进行归一化。

Alternate Interface备用接口

出于各种原因，包括与遗留代码的兼容性，NumericDiffCostFunction也可以将CostFunction对象作为输入。下面描述如何做到这一点。

要获得数值微分的代价函数，定义CostFunction的子类，这样CostFunction::Evaluate()函数就会忽略雅可比矩阵参数。
数值微分封装将在必要时通过反复调用CostFunction::Evaluate()来填充雅可比矩阵参数，并对适当的参数进行微小的更改，并计算斜率。
为了提高性能，数值差异封装类是在具体的成本函数上模板化的，尽管它只能根据CostFunction接口实现。

代价函数的数值微分形式可以构造为:

CostFunction* cost_function
    = new NumericDiffCostFunction<MyCostFunction, CENTRAL, 1, 4, 8>(
        new MyCostFunction(...), TAKE_OWNERSHIP);

其中MyCostFunction有1个残差和2个大小分别为4和8的参数块。查看测试以获得更详细的示例。

6.DynamicNumericDiffCostFunction


与AutoDiffCostFunction一样，NumericDiffCostFunction要求在编译时知道参数块的数量和大小。在许多应用中，这是不够的。

template <typename CostFunctor, NumericDiffMethodType method = CENTRAL>
class DynamicNumericDiffCostFunction : public CostFunction {
};

在需要数值微分的情况下，可以使用DynamicNumericDiffCostFunction。
与NumericDiffCostFunction一样，用户必须定义一个仿函数，但是仿函数的声明略有不同。cost functors的预期接口是:

struct MyCostFunctor {
  bool operator()(double const* const* parameters, double* residuals) const {
  }
}

由于参数的大小在运行时是已知的，因此必须在创建动态数值微分成本函数之后指定大小。例如:

DynamicNumericDiffCostFunction<MyCostFunctor>* cost_function =
  new DynamicNumericDiffCostFunction<MyCostFunctor>(new MyCostFunctor);
cost_function->AddParameterBlock(5);
cost_function->AddParameterBlock(10);
cost_function->SetNumResiduals(21);

作为一条经验法则，在使用DynamicNumericDiffCostFunction之前尝试使用NumericDiffCostFunction。
与NumericDiffCostFunction一样，在混合局部参数与数值微分时也要小心。

7.CostFunctionToFunctor


CostFunctionToFunctor是一个适配器类，允许用户在模板化的仿函数中使用CostFunction对象，用于自动微分。这允许用户无缝地混合解析，数值和自动微分。

例如，让我们假设

class IntrinsicProjection : public SizedCostFunction<2, 5, 3> {
  public:
    IntrinsicProjection(const double* observation);
    virtual bool Evaluate(double const* const* parameters,
                          double* residuals,
                          double** jacobians) const;
};

是一个CostFunction，它实现局部坐标系中的一个点投影到它的图像平面上，并从观测到的点投影中减去它。它可以计算残差并且通过解析微分或数值微分计算雅可比矩阵。

现在我们想将这个CostFunction的行为与摄像机外参的行为组合起来，即旋转和平移。假设我们有一个模板化的函数

template<typename T>
void RotateAndTranslatePoint(const T* rotation,
                             const T* translation,
                             const T* point,
                             T* result);

然后我们可以这样做，

struct CameraProjection {
  CameraProjection(double* observation)
  : intrinsic_projection_(new IntrinsicProjection(observation)) {
  }

  template <typename T>
  bool operator()(const T* rotation,
                  const T* translation,
                  const T* intrinsics,
                  const T* point,
                  T* residual) const {
    T transformed_point[3];
    RotateAndTranslatePoint(rotation, translation, point, transformed_point);

    // Note that we call intrinsic_projection_, just like it was
    // any other templated functor.
    return intrinsic_projection_(intrinsics, transformed_point, residual);
  }

 private:
  CostFunctionToFunctor<2,5,3> intrinsic_projection_;
};

注意，CostFunctionToFunctor接受传递给构造函数的CostFunction的所有权。

在上面的例子中，我们假设IntrinsicProjection是一个能够计算其值和导数的成本函数。如果不是这样，则定义IntrinsicProjection如下:

struct IntrinsicProjection {
  IntrinsicProjection(const double* observation) {
    observation_[0] = observation[0];
    observation_[1] = observation[1];
  }

  bool operator()(const double* calibration,
                  const double* point,
                  double* residuals) const {
    double projection[2];
    ThirdPartyProjectionFunction(calibration, point, projection);
    residuals[0] = observation_[0] - projection[0];
    residuals[1] = observation_[1] - projection[1];
    return true;
  }
  double observation_[2];
};

这里的ThirdPartyProjectionFunction是我们无法控制的第三方库函数。这个函数可以计算它的值，并且我们想用数值微分来计算它的导数。
在本例中，我们可以使用NumericDiffCostFunction和CostFunctionToFunctor的组合来完成工作。

struct CameraProjection {
  CameraProjection(double* observation)
     : intrinsic_projection_(
           new NumericDiffCostFunction<IntrinsicProjection, CENTRAL, 2, 5, 3>(
               new IntrinsicProjection(observation))) {}

  template <typename T>
  bool operator()(const T* rotation,
                  const T* translation,
                  const T* intrinsics,
                  const T* point,
                  T* residuals) const {
    T transformed_point[3];
    RotateAndTranslatePoint(rotation, translation, point, transformed_point);
    return intrinsic_projection_(intrinsics, transformed_point, residuals);
  }

 private:
  CostFunctionToFunctor<2, 5, 3> intrinsic_projection_;
};

8.DynamicCostFunctionToFunctor

DynamicCostFunctionToFunctor提供了与CostFunctionToFunctor相同的功能，用于在编译时不知道参数向量和残差的数量和大小的情况。DynamicCostFunctionToFunctor提供的API与DynamicAutoDiffCostFunction所期望的匹配，即它提供了一个模板化的仿函数:

template<typename T>
bool operator()(T const* const* parameters, T* residuals) const;

类似于CostFunctionToFunctor的例子，让我们假设

class IntrinsicProjection : public CostFunction {
  public:
    IntrinsicProjection(const double* observation);
    virtual bool Evaluate(double const* const* parameters,
                          double* residuals,
                          double** jacobians) const;
};

是一个CostFunction，它将其局部坐标系中的一个点投影到图像平面上，并从观测到的点投影中减去该点。

在模板化的仿函数中使用这个CostFunction会是这样的:

struct CameraProjection {
  CameraProjection(double* observation)
      : intrinsic_projection_(new IntrinsicProjection(observation)) {
  }

  template <typename T>
  bool operator()(T const* const* parameters,
                  T* residual) const {
    const T* rotation = parameters[0];
    const T* translation = parameters[1];
    const T* intrinsics = parameters[2];
    const T* point = parameters[3];

    T transformed_point[3];
    RotateAndTranslatePoint(rotation, translation, point, transformed_point);

    const T* projection_parameters[2];
    projection_parameters[0] = intrinsics;
    projection_parameters[1] = transformed_point;
    return intrinsic_projection_(projection_parameters, residual);
  }

 private:
  DynamicCostFunctionToFunctor intrinsic_projection_;
};

像CostFunctionToFunctor一样，DynamicCostFunctionToFunctor获得传递给构造函数的CostFunction的所有权。

9.ConditionedCostFunction

这个类允许对封装的成本函数的残差值应用不同的条件。一个例子,这是有用的是,您有一个现有的成本函数产生N值,但你想要的总成本是除了这些平方值的总和,也许你想要应用不同的缩放值,改变他们对成本的贡献。

//  my_cost_function produces N residuals
CostFunction* my_cost_function = ...
CHECK_EQ(N, my_cost_function->num_residuals());
vector<CostFunction*> conditioners;

//  Make N 1x1 cost functions (1 parameter, 1 residual)
CostFunction* f_1 = ...
conditioners.push_back(f_1);

CostFunction* f_N = ...
conditioners.push_back(f_N);
ConditionedCostFunction* ccf =
  new ConditionedCostFunction(my_cost_function, conditioners);


ccf_residual[i] = f_i(my_cost_function_residual[i])

雅可比矩阵会受到适当的影响。

posted on 2021-09-28 17:41  JJ_S  阅读(1213)  评论(0)  编辑  收藏  举报

Powered by: 博客园 Copyright © 2024 JJ_S
Powered by .NET 9.0 on Kubernetes