12.Ceres官方教程-On Derivatives~Interfacing with Automatic Differentiation
在成本函数的显式表达式可用的情况下,自动微分很容易使用。通常程序都需要与外部的程序或数据进行交互。在本章中,我们将考虑几种不同的方法。
为此,我们将考虑寻找参数θ和t的问题,以解决以下形式的优化问题:
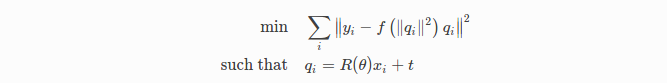
这里,R是一个用角度θ参数化的二维旋转矩阵,t是一个二维向量。f是一个外部畸变函数。
我们首先考虑这种情况,我们有一个模板化的函数TemplatedComputeDistortion,它可以计算函数f。然后,相应残差仿函数的实现就很简单了,如下所示:
template <typename T> T TemplatedComputeDistortion(const T r2) {
const double k1 = 0.0082;
const double k2 = 0.000023;
return 1.0 + k1 * r2 + k2 * r2 * r2;
}
struct Affine2DWithDistortion {
Affine2DWithDistortion(const double x_in[2], const double y_in[2]) {
x[0] = x_in[0];
x[1] = x_in[1];
y[0] = y_in[0];
y[1] = y_in[1];
}
template <typename T>
bool operator()(const T* theta,
const T* t,
T* residuals) const {
const T q_0 = cos(theta[0]) * x[0] - sin(theta[0]) * x[1] + t[0];
const T q_1 = sin(theta[0]) * x[0] + cos(theta[0]) * x[1] + t[1];
const T f = TemplatedComputeDistortion(q_0 * q_0 + q_1 * q_1);
residuals[0] = y[0] - f * q_0;
residuals[1] = y[1] - f * q_1;
return true;
}
double x[2];
double y[2];
};
到目前为止还不错,但现在让我们考虑三种定义f的方法,它们不能直接用于自动微分:
1.计算其值的非模板函数。
2.求其值和导数的函数。
3.定义为要内插的值表的函数。
我们将在下面依次考虑它们。
1.A function that returns its value
假设我们给定一个函数ComputeDistortionValue,声明如下:
double ComputeDistortionValue(double r2);
计算f的值。函数的实际实现并不重要。将这个函数与Affine2DWithDistortion对接起来有三个步骤:
1.把ComputeDistortionValue封装成函数ComputeDistortionValueFunctor。
2.对ComputeDistortionValueFunctor使用NumericDiffCostFunction进行数值微分,从而创建CostFunction
3.使用CostFunctionToFunctor封装CostFunction。封装后得到一个带有模板化操作符operator()的函数。这个操作符operator()方法可以将NumericDiffCostFunction计算出的雅可比矩阵变成Jet对象。
上述三个步骤的实现如下所示:
struct ComputeDistortionValueFunctor {
bool operator()(const double* r2, double* value) const {
*value = ComputeDistortionValue(r2[0]);
return true;
}
};
struct Affine2DWithDistortion {
Affine2DWithDistortion(const double x_in[2], const double y_in[2]) {
x[0] = x_in[0];
x[1] = x_in[1];
y[0] = y_in[0];
y[1] = y_in[1];
compute_distortion.reset(new ceres::CostFunctionToFunctor<1, 1>(
new ceres::NumericDiffCostFunction<ComputeDistortionValueFunctor,
ceres::CENTRAL,
1,
1>(
new ComputeDistortionValueFunctor)));
}
template <typename T>
bool operator()(const T* theta, const T* t, T* residuals) const {
const T q_0 = cos(theta[0]) * x[0] - sin(theta[0]) * x[1] + t[0];
const T q_1 = sin(theta[0]) * x[0] + cos(theta[0]) * x[1] + t[1];
const T r2 = q_0 * q_0 + q_1 * q_1;
T f;
(*compute_distortion)(&r2, &f);
residuals[0] = y[0] - f * q_0;
residuals[1] = y[1] - f * q_1;
return true;
}
double x[2];
double y[2];
std::unique_ptr<ceres::CostFunctionToFunctor<1, 1> > compute_distortion;
};
2.A function that returns its value and derivative
现在假设我们有一个函数ComputeDistortionValue,可以得到它的值,并且可以根据需要获取其雅可比矩阵。其函数声明如下:
void ComputeDistortionValueAndJacobian(double r2,
double* value,
double* jacobian);
同样,函数的实际实现并不重要。将这个函数与Affine2DWithDistortion对接起来需要两个步骤:
1.把ComputeDistortionValueAndJacobian封装到一个CostFunction对象内。这个CostFunction对象我们称为ComputeDistortionFunction。
2.用CostFunctionToFunctor封装刚刚得到的ComputeDistortionFunction对象。得到一个带有模板操作符operator()方法的Functor,它将由NumericDiffCostFunction计算出的雅可比矩阵变成适合Jet对象。
代码如下:
class ComputeDistortionFunction : public ceres::SizedCostFunction<1, 1> {
public:
virtual bool Evaluate(double const* const* parameters,
double* residuals,
double** jacobians) const {
if (!jacobians) {
ComputeDistortionValueAndJacobian(parameters[0][0], residuals, nullptr);
} else {
ComputeDistortionValueAndJacobian(parameters[0][0], residuals, jacobians[0]);
}
return true;
}
};
struct Affine2DWithDistortion {
Affine2DWithDistortion(const double x_in[2], const double y_in[2]) {
x[0] = x_in[0];
x[1] = x_in[1];
y[0] = y_in[0];
y[1] = y_in[1];
compute_distortion.reset(
new ceres::CostFunctionToFunctor<1, 1>(new ComputeDistortionFunction));
}
template <typename T>
bool operator()(const T* theta,
const T* t,
T* residuals) const {
const T q_0 = cos(theta[0]) * x[0] - sin(theta[0]) * x[1] + t[0];
const T q_1 = sin(theta[0]) * x[0] + cos(theta[0]) * x[1] + t[1];
const T r2 = q_0 * q_0 + q_1 * q_1;
T f;
(*compute_distortion)(&r2, &f);
residuals[0] = y[0] - f * q_0;
residuals[1] = y[1] - f * q_1;
return true;
}
double x[2];
double y[2];
std::unique_ptr<ceres::CostFunctionToFunctor<1, 1> > compute_distortion;
};
3.A function that is defined as a table of values
我们将考虑的第三种也是最后一种情况是,函数f定义为区间[0,100]上的值表,每个整数都有一个值。
vector<double> distortion_values;
有许多方法可以插入值表。也许最简单和最常见的方法是线性插值。但是使用线性插值并不是一个好主意,因为插值函数在采样点是不可微的。
另一个简单但是性能优异的可微插值方法是 Cubic Hermite Spline(中文埃尔米特插值) Ceres提供Cubic和Bi-Cubic插值的整个流程,并且可以很方便的应用自动微分算法。
使用Cubic插值需要首先构造一个Grid1D对象来封装值表,然后使用它构造一个CubicInterpolator对象。
结果代码如下所示:
struct Affine2DWithDistortion {
Affine2DWithDistortion(const double x_in[2],
const double y_in[2],
const std::vector<double>& distortion_values) {
x[0] = x_in[0];
x[1] = x_in[1];
y[0] = y_in[0];
y[1] = y_in[1];
grid.reset(new ceres::Grid1D<double, 1>(
&distortion_values[0], 0, distortion_values.size()));
compute_distortion.reset(
new ceres::CubicInterpolator<ceres::Grid1D<double, 1> >(*grid));
}
template <typename T>
bool operator()(const T* theta,
const T* t,
T* residuals) const {
const T q_0 = cos(theta[0]) * x[0] - sin(theta[0]) * x[1] + t[0];
const T q_1 = sin(theta[0]) * x[0] + cos(theta[0]) * x[1] + t[1];
const T r2 = q_0 * q_0 + q_1 * q_1;
T f;
compute_distortion->Evaluate(r2, &f);
residuals[0] = y[0] - f * q_0;
residuals[1] = y[1] - f * q_1;
return true;
}
double x[2];
double y[2];
std::unique_ptr<ceres::Grid1D<double, 1> > grid;
std::unique_ptr<ceres::CubicInterpolator<ceres::Grid1D<double, 1> > > compute_distortion;
};
在上面的例子中,我们使用Grid1D和CubicInterpolator来插值一个一维的值表。Grid2D与CubicInterpolator结合使用,用户可以插入二维的值表。注意,Grid1D或Grid2D都不限于标量值函数,它们还可以使用向量值函数。





