3.Ceres官方教程-非线性最小二乘～Powell’s Function(鲍威尔方程)
考虑一个稍微复杂一点的例子 – 求解鲍威尔方程的最小值。我们定义参数块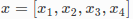
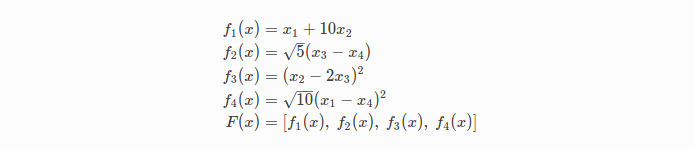
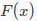是关于上面四个残差值的方程。我们希望寻找到一组x，使
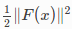最小。
同样，第一步是定义目标函数中的每一项需评估的仿函数，以评估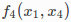
的代码为例
struct F4 {
template <typename T>
bool operator()(const T* const x1, const T* const x4, T* residual) const {
residual[0] = sqrt(10.0) * (x1[0] - x4[0]) * (x1[0] - x4[0]);
return true;
}
};
类似地，我们也可以分别地定义类F1，F2，F3取评估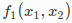
，
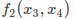和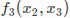
使用这些，问题可以构造如下:
double x1 = 3.0; double x2 = -1.0; double x3 = 0.0; double x4 = 1.0;
Problem problem;
// Add residual terms to the problem using the using the autodiff
// wrapper to get the derivatives automatically.
problem.AddResidualBlock(
new AutoDiffCostFunction<F1, 1, 1, 1>(new F1), nullptr, &x1, &x2);
problem.AddResidualBlock(
new AutoDiffCostFunction<F2, 1, 1, 1>(new F2), nullptr, &x3, &x4);
problem.AddResidualBlock(
new AutoDiffCostFunction<F3, 1, 1, 1>(new F3), nullptr, &x2, &x3)
problem.AddResidualBlock(
new AutoDiffCostFunction<F4, 1, 1, 1>(new F4), nullptr, &x1, &x4);
注意，每个ResidualBlock只依赖于对应残差对象所依赖的两个参数，而不是所有四个参数
实例代码在ceres-solver-1.14.0/examples/powell.cc中
#include <vector>
#include "ceres/ceres.h"
#include "gflags/gflags.h"
#include "glog/logging.h"
using ceres::AutoDiffCostFunction;
using ceres::CostFunction;
using ceres::Problem;
using ceres::Solver;
using ceres::Solve;
struct F1 {
template <typename T> bool operator()(const T* const x1,
const T* const x2,
T* residual) const {
// f1 = x1 + 10 * x2;
residual[0] = x1[0] + 10.0 * x2[0];
return true;
}
};
struct F2 {
template <typename T> bool operator()(const T* const x3,
const T* const x4,
T* residual) const {
// f2 = sqrt(5) (x3 - x4)
residual[0] = sqrt(5.0) * (x3[0] - x4[0]);
return true;
}
};
struct F3 {
template <typename T> bool operator()(const T* const x2,
const T* const x3,
T* residual) const {
// f3 = (x2 - 2 x3)^2
residual[0] = (x2[0] - 2.0 * x3[0]) * (x2[0] - 2.0 * x3[0]);
return true;
}
};
struct F4 {
template <typename T> bool operator()(const T* const x1,
const T* const x4,
T* residual) const {
// f4 = sqrt(10) (x1 - x4)^2
residual[0] = sqrt(10.0) * (x1[0] - x4[0]) * (x1[0] - x4[0]);
return true;
}
};
// DEFINE_string(minimizer, "trust_region",
// "Minimizer type to use, choices are: line_search & trust_region");
int main(int argc, char** argv) {
// CERES_GFLAGS_NAMESPACE::ParseCommandLineFlags(&argc, &argv, true);
// google::InitGoogleLogging(argv[0]);
double x1 = 3.0;
double x2 = -1.0;
double x3 = 0.0;
double x4 = 1.0;
Problem problem;
// Add residual terms to the problem using the using the autodiff
// wrapper to get the derivatives automatically. The parameters, x1 through
// x4, are modified in place.
problem.AddResidualBlock(new AutoDiffCostFunction<F1, 1, 1, 1>(new F1),
NULL,
&x1, &x2);
problem.AddResidualBlock(new AutoDiffCostFunction<F2, 1, 1, 1>(new F2),
NULL,
&x3, &x4);
problem.AddResidualBlock(new AutoDiffCostFunction<F3, 1, 1, 1>(new F3),
NULL,
&x2, &x3);
problem.AddResidualBlock(new AutoDiffCostFunction<F4, 1, 1, 1>(new F4),
NULL,
&x1, &x4);
Solver::Options options;
// LOG_IF(FATAL, !ceres::StringToMinimizerType(FLAGS_minimizer,
// &options.minimizer_type))
// << "Invalid minimizer: " << FLAGS_minimizer
// << ", valid options are: trust_region and line_search.";
options.max_num_iterations = 100;
options.linear_solver_type = ceres::DENSE_QR;
options.minimizer_progress_to_stdout = true;
std::cout << "Initial x1 = " << x1
<< ", x2 = " << x2
<< ", x3 = " << x3
<< ", x4 = " << x4
<< "\n";
// Run the solver!
Solver::Summary summary;
Solve(options, &problem, &summary);
std::cout << summary.FullReport() << "\n";
std::cout << "Final x1 = " << x1
<< ", x2 = " << x2
<< ", x3 = " << x3
<< ", x4 = " << x4
<< "\n";
return 0;
}
结果
Initial x1 = 3, x2 = -1, x3 = 0, x4 = 1
iter cost cost_change |gradient| |step| tr_ratio tr_radius ls_iter iter_time total_time
0 1.075000e+02 0.00e+00 1.55e+02 0.00e+00 0.00e+00 1.00e+04 0 4.00e-05 2.61e-04
1 5.036190e+00 1.02e+02 2.00e+01 2.16e+00 9.53e-01 3.00e+04 1 9.81e-05 3.78e-04
2 3.148168e-01 4.72e+00 2.50e+00 6.23e-01 9.37e-01 9.00e+04 1 2.29e-05 4.08e-04
3 1.967760e-02 2.95e-01 3.13e-01 3.08e-01 9.37e-01 2.70e+05 1 3.73e-05 4.71e-04
4 1.229900e-03 1.84e-02 3.91e-02 1.54e-01 9.37e-01 8.10e+05 1 7.39e-05 5.51e-04
5 7.687123e-05 1.15e-03 4.89e-03 7.69e-02 9.37e-01 2.43e+06 1 7.08e-05 6.27e-04
6 4.804625e-06 7.21e-05 6.11e-04 3.85e-02 9.37e-01 7.29e+06 1 5.50e-05 6.87e-04
7 3.003028e-07 4.50e-06 7.64e-05 1.92e-02 9.37e-01 2.19e+07 1 5.54e-05 7.47e-04
8 1.877006e-08 2.82e-07 9.54e-06 9.62e-03 9.37e-01 6.56e+07 1 2.07e-05 7.92e-04
9 1.173223e-09 1.76e-08 1.19e-06 4.81e-03 9.37e-01 1.97e+08 1 2.31e-05 8.20e-04
10 7.333425e-11 1.10e-09 1.49e-07 2.40e-03 9.37e-01 5.90e+08 1 5.54e-05 8.81e-04
11 4.584044e-12 6.88e-11 1.86e-08 1.20e-03 9.37e-01 1.77e+09 1 2.08e-05 9.08e-04
12 2.865573e-13 4.30e-12 2.33e-09 6.02e-04 9.37e-01 5.31e+09 1 2.06e-05 9.33e-04
13 1.791438e-14 2.69e-13 2.91e-10 3.01e-04 9.37e-01 1.59e+10 1 2.07e-05 9.59e-04
14 1.120029e-15 1.68e-14 3.64e-11 1.51e-04 9.37e-01 4.78e+10 1 2.06e-05 9.85e-04
trust_region_minimizer.cc:649 Terminating: Gradient tolerance reached. Gradient max norm: 3.642190e-11 <= 1.000000e-10
Solver Summary (v 1.14.0-eigen-(3.3.7)-no_lapack-eigensparse-openmp-no_tbb-no_custom_blas)
Original Reduced
Parameter blocks 4 4
Parameters 4 4
Residual blocks 4 4
Residuals 4 4
Minimizer TRUST_REGION
Dense linear algebra library EIGEN
Trust region strategy LEVENBERG_MARQUARDT
Given Used
Linear solver DENSE_QR DENSE_QR
Threads 1 1
Linear solver ordering AUTOMATIC 4
Cost:
Initial 1.075000e+02
Final 1.120029e-15
Change 1.075000e+02
Minimizer iterations 15
Successful steps 15
Unsuccessful steps 0
Time (in seconds):
Preprocessor 0.000221
Residual only evaluation 0.000062 (14)
Jacobian & residual evaluation 0.000403 (15)
Linear solver 0.000057 (14)
Minimizer 0.000823
Postprocessor 0.000004
Total 0.001048
Termination: CONVERGENCE (Gradient tolerance reached. Gradient max norm: 3.642190e-11 <= 1.000000e-10)
Final x1 = 0.000146222, x2 = -1.46222e-05, x3 = 2.40957e-05, x4 = 2.40957e-05
很容易看出，这个问题的最优解是在x1=0,x2=0,x3=0,x4=0时，目标函数值为0。
