齐次坐标 ---向量叉乘, 无穷远点
1.背景
笛卡尔坐标系: 就是直角坐标系和斜坐标系的统称。
欧氏空间:
在欧氏(几何)空间,同一平面的两条平行线永远不能相交,这是我们都熟悉的一种场景。 然而,在透视空间里面,两条平行线可以相交,例如:火车轨道随着我们的视线越来越窄,最后两条平行线在无穷远处交于一点。

欧氏空间(或者笛卡尔空间)描述2D/3D几何非常适合,但是这种方法却不适合处理透视空间的问题(实际上,欧氏几何是透视几何的一个子集合),2D笛卡尔坐标可以表示为(x,y) 。
如果一个点在无穷远处,这个点的坐标将会(∞,∞),在欧氏空间中,这就变得没有意义。平行线在透视空间的无穷远处交于一点,但是在欧氏空间却不能表示,数学家发现了一种方式来解决这个问题(那就是齐次坐标)。
2.齐次坐标的定义
“齐次坐标表示是计算机图形学的重要手段之一,它既能够用来明确区分向量和点,同时也更易用于进行仿射(线性)几何变换。”—— F.S. Hill, JR
简单的说:齐次坐标就是在原有坐标上加上一个维度:
我们可以在一个2D笛卡尔坐标末尾加上一个额外的变量w来形成2D齐次坐标。因此,一个在笛卡尔坐标系下的点(X, Y)在齐次坐标里面变成了(x, y,w),并且有
X = x/w
Y = y/w
例如,笛卡尔坐标系下(1,2)齐次坐标可以表示为(1,2,1),如果点(1,2)移动到无限远处,在笛卡尔坐标下它变为(∞,∞),然后它的齐次坐标表示为(1,2,0),因为(1/0,2/0)=(∞,∞)。
注意这样的话,我们可以不用 ” ∞ " 来表示一个无穷远处的点了
3.点和向量
点是三维空间中的某个坐标,是绝对的,它的值是参照原点的。
向量用于表示力和速度等具有方向和大小的量, 通常用具有长度和方向的线段来表示。
他们都具有三个分量,但对于向量,如果将向量放在坐标系中的任何位置(平移),都不会改变其性质,因为向量表示的是方向和大小,与位置距离无关,它的值是相对与基准点的。下图是三维顶点和向量的数学符号或称为列矩阵。
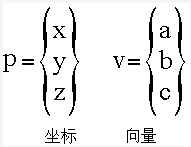
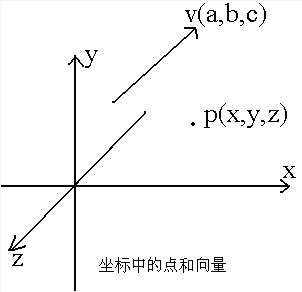
两个点向量得到一个向量:
设O(0,0)是原点,则A、B的坐标与向量OA、OB的坐标相同,向量BA=向量OB-向量OA
点和向量转为齐次坐标, 通过将第四个分量定义为0或1,来描述前面三个坐标分量是向量的还是点的坐标。
1.如果第四个分量为 0,则前面 x,y,z 三个坐标分量描述的是一个向量。
2.如果第四个分量为 1,则前面 x,y,z 三个坐标分量描述的是一个点。
普通坐标(Ordinary Coordinate)和齐次坐标(Homogeneous Coordinate)之间进行转换:
(1)从普通坐标转换成齐次坐标时
如果(x,y,z)是个点,则变为(x,y,z,1);
如果(x,y,z)是个向量,则变为(x,y,z,0)
(2)从齐次坐标转换成普通坐标时
如果是(x,y,z,1),则知道它是个点,变成(x,y,z);
如果是(x,y,z,0),则知道它是个向量,仍然变成(x,y,z)
通过定义,我们同时得到以下性质:
1)两点相减的结果是一个向量(因为两个点第四个分量都为 1,相减之后变为了 0)
2)一个点与一个向量相加的结果是一个点(点的第四个分量为 1,而向量的第四个分量为 0,1+0=1,因此相加的结果是一个点)
4.无穷远点
在平面几何中,我们认为“平行直线不会相交”。这个观点在射影几何中得到了修正,“平行直线相交于无穷远点”。无穷远点并不在我们通常理解的平面之内,而是在平面之外的“无穷远处”。为了方便说明,这种点通常用∞
来表示。
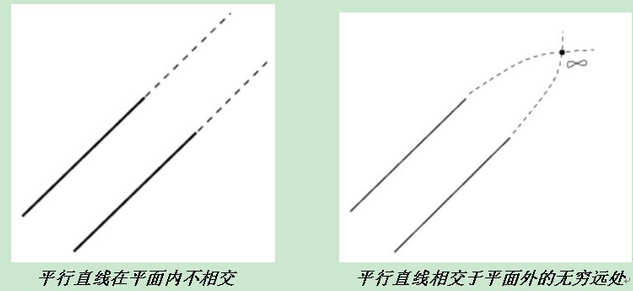
用齐次坐标证明两条平行直线相交于无穷远点
在欧几里得空间的线性系统方程:
两条平行直线:
Ax + By + C = 0
Ax + By + D = 0
在笛卡尔坐标系中,如果C≠D该方程组无解。如果C=D,两条直线就相同了。
在透视空间中,使用齐次坐标“(x/w, y/w)"分别代替(x, y)重写这个方程。
Ax/w + By/w + C = 0
Ax/w + By/w + D = 0
化为
Ax + By + Cw = 0
Ax + By + Dw = 0
有一个解(x,y,0)。因此两条平行直线相交于(x,y,0),这个点在无穷远处。
在二维向量中,点的齐次坐标表示为(x,y,1),写成一般形式为(Hx,Hy,H)。对于任何不等于0的H,(Hx,Hy,H)都表示普通坐标中的(x,y),所以在二/三维空间中,点没有唯一的齐次坐标。
例如,齐次坐标(12,9,3)和(8,6,2)都表示普通坐标系中的一点(4,3)。当齐次坐标已知时,若要求解普通坐标(x,y)时,可用H除各个齐次坐标,这个过程称为标准化(或称正常化)。
引入齐次坐标后,可以用齐次坐标表示无穷远点,例如
(1,0,0)可以表示x方向的无穷远点
(0,1,0)可以表示y方向的无穷远点
可以通过透视变换将无穷远处的点变换为与之对应的有限远点,相当于透视投影中的灭点。
5.叉乘--点与点,直线与直线
点与点的叉乘
结论:在齐次坐标下,可以用两个点 p, q 的齐次坐标叉乘结果来表达一条直线 l,也就是
直线l = 点p x 点q
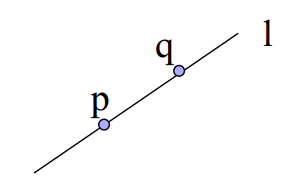
直线与直线的叉乘
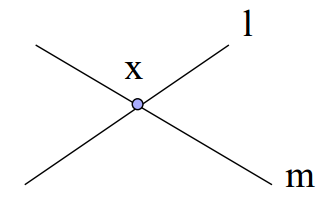
结论:在齐次坐标下,两条直线 l, m 的叉乘表示他们的交点 x
交点x = 直线l x 直线m
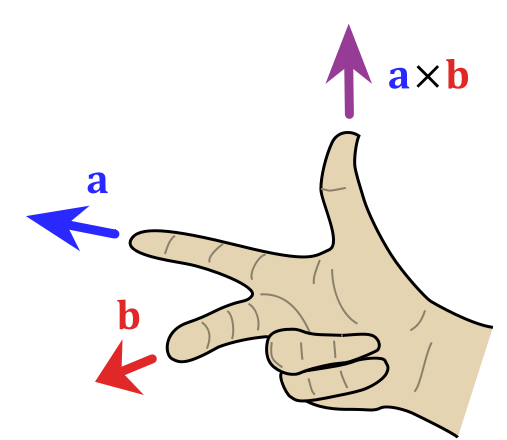
两个向量叉乘的方向
两个向量a和b的叉乘仅在三维空间中有定义,写作 a x b. a x b 是与向量a, b都垂直的向量,其方向通过右手定则(见下图)决定。
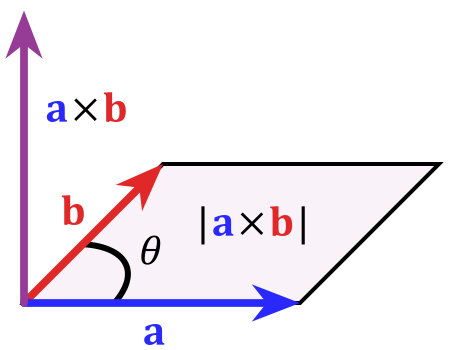
其模长等于以两个向量为边的平行四边形的面积(见下图)。
证明
为什么两条直线 l, m 的叉乘 l x m 等于它们的交点 p,也就是 p = l x m?
原因如下:首先,根据前面叉乘的定义,l x m 的结果向量(记为 p = l x m) 与 l 和 m都垂直,根据点乘的定义,垂直的向量之间的点积为0,因此可以得到:
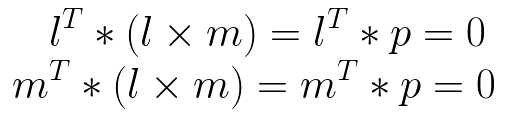
因此,根据前面点在直线上的结论,可以看到p既在直线l上又在直线m上,所以p = l x m是两条直线的交点。此处p是齐次坐标。同样的,可以证明,两点p, q 的叉乘 可以表示 过两点的直线l,即 l = p x q。
参考
https://zhuanlan.zhihu.com/p/373969867
https://www.cnblogs.com/CodeBlove/archive/2008/10/25/1319563.html
https://www.cnblogs.com/csyisong/archive/2008/12/09/1351372.html
https://jingyan.baidu.com/article/2c8c281dd30bb50008252a03.html
无穷远点参考
http://www.360doc.com/content/18/0313/11/9200790_736608542.shtml
http://www.360doc.com/content/18/0313/11/9200790_736608542.shtml
叉乘参考
https://blog.csdn.net/yinfourever/article/details/98480841



