k近邻算法以及kd树的实现

基本思想

k近邻算法用于分类，训练数据离散的分布在n维空间中，当有一个未知类别新数据到来

1. 在n维空间中找到和他最近的k个点（最相似的
2. 这k个点按照类别划分，成员最多的类别代表新数据的类别，起到预测的效果。即近朱者赤近墨者黑。

距离度量

上诉思想中需要寻找最近的点，通常使用欧式距离

分类决策

选出k个最近的点之后，马上要进行多数表决

具体实现-kd树

当了解了具体思想之后，自然而然想到每次进行数组遍历，但是当训练数据特征较多，数量较大时，单纯的线性遍历会进行大量的不必要的运算，因此考虑提前将训练数据进行处理，变得有规律，所以引入了kd tree

那么为什么kdtree能提高速度呢？

kd树（k-dimensional树的简称），是一种对k维空间中的实例点进行存储以便对其进行快速搜索的二叉树结构。利用kd树可以省去对大部分数据点的搜索，从而减少搜索的计算量。

kd树广泛应用于数据库中，数据库中的元组通常都是多维的

kd树的构建

• 首先看一维（只有一个属性）的例子，构造平衡二叉树即可解决

• 二维数据

  • 思路一：分别构造两棵avl树，然后查询的集合取交集。

  • 思路二：构建kd树

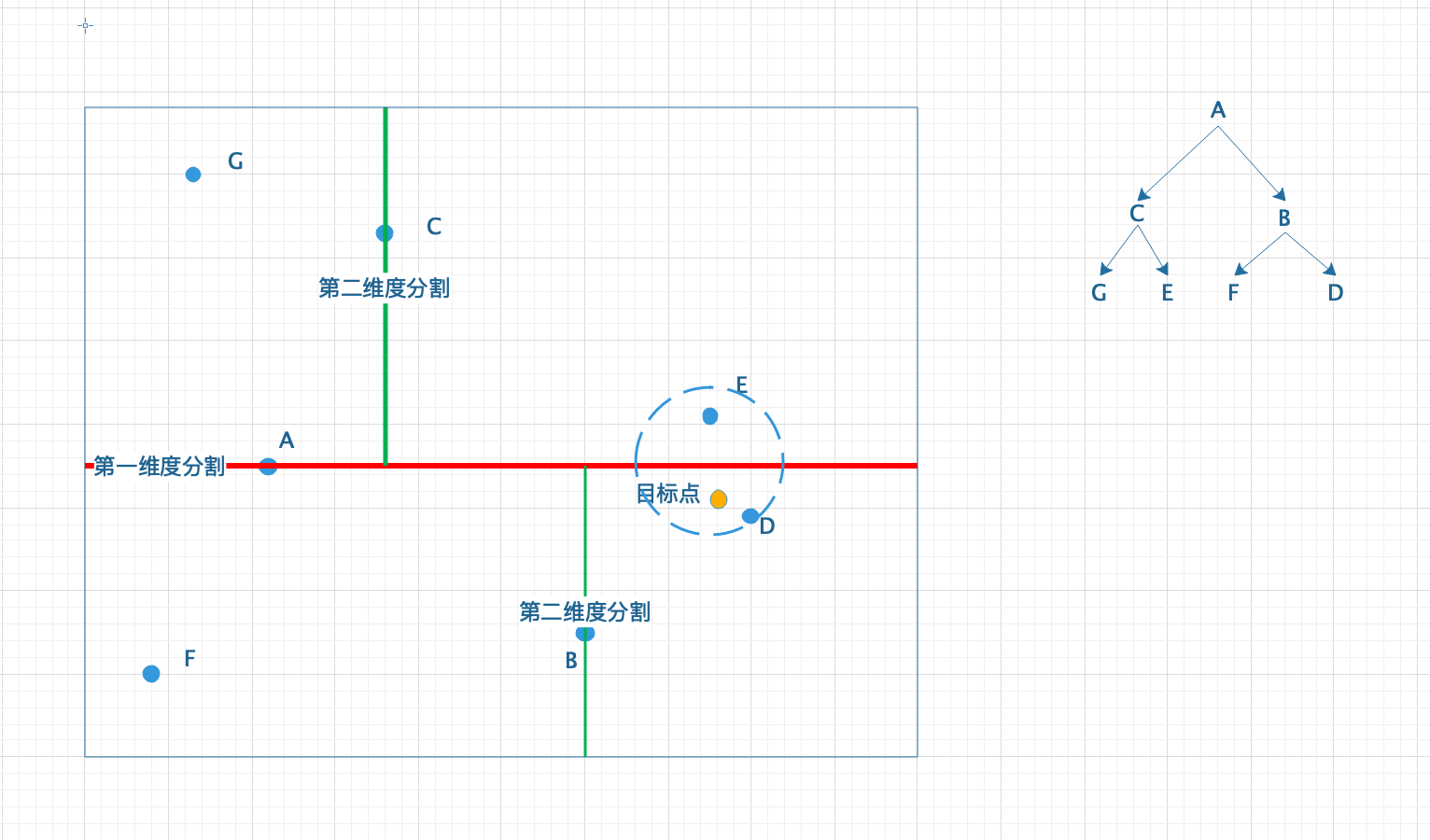
    • 对节点进行排序，取第i维数据的中值
      $$
      mid = length/2
      $$
      作为根节点，小于中值的放在左子节点，大于中值的放在右子节点，然后下一层kd树上利用第i+1维进行递归的划分。维度可以循环使用，知道不可再继续划分。

kd树的搜索

1. 同一层的节点都是按照相同的维度进行划分的，因此搜索目标点X的最近节点需要从根节点出发，根据该层对应的维度i进行查找，小于根点在维度i上的值时，递归的查询左节点，否则查询右节点。遇到叶结点停止，以此叶结点为当前最近邻点，叶结点记作S，距离记作D，S不一定是最终结果，但是如果有更优的点，此点必然出现在以X为中心半径为D的圆当中。
2. 回溯到父节点，判断S的兄弟节点代表的区域是否与以X为中心半径为D的圆相交，如果相交的话，区域里面的点就有可能在圆内，成为更优的点，因此要递归的进行搜索兄弟子树，看是否存在在圆内的点，存在的话就更新圆。反之，不相交就没有必要去搜索该子树，避开了进行无意义的搜索，从而提高了搜索效率。不相交时，需要继续向上回溯。
3.