1067A - Array Without Local Maximums

题目大意

　　有一串长度为$n$的数字，其中由一些数字看不清了（$-1$的数字就是看不清的），而这些数字取值范围满足$0\leq a \leq20 $，问满足一下条件

$(1) a_{1}\leq a_{2}$

$(2) a_{n}\leq a_{n-1}$

$(3) a_{i}\leq max(a_{i-1},a_{i+1}) i\in [2,n-1]$

的方案数有多少种.

分析

　　dp。$dp[i][num][flag]=$第$i$个数字为$num$，$(1) flag=0$时，表示$a_{i-1}< a_{i}$,$(2) flag=1$时，表示$a_{i-1}\geq a_{i}$的方案数。可能有人会有点疑问，为什么这样定义，看下面几张图

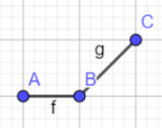
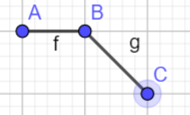
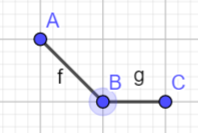
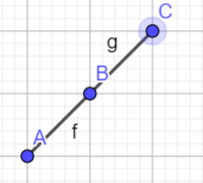
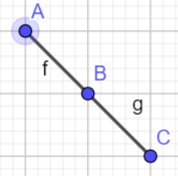
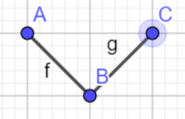
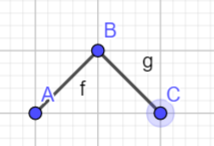
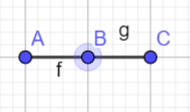
根据条件，连续的3个点是互相关联的，如果我们将这三个连续的写为$A,B,C$如果想让$C$合法，由上面的图上我们得到由$B\geq C且A\geq C$和$C>B$这样两种情况得到，然后再根据$flag$的定义，我们可以得到以下状态转移方程$dp[i][num][0]=\sum_{j=1}^{num-1} (dp[i-1][j][1]+dp[i-1][j][0])$和$dp[i][num][1]=dp[i][num][0]+\sum_{j=num}^{200} {dp[i-1][j][1]}$,这里$num$的两种情况的转移方程并不差别。但是如果这样做复杂度是$O_{(n\cdot num \cdot num)}$我们可以通过前缀和和后缀和，将复杂度变成$O_{(n\cdot num)}$详细看代码

#define frp

#include<bits/stdc++.h>
#include <algorithm>
#include <cmath>
#include <iostream>
#include <cstring>
#include <string>
#include <string.h>
#include <iomanip>

using namespace std;
typedef long long ll;
const ll INF = 0x3f3f3f3f;
const ll inf = 0x7fffff;
const int maxn = 2e6;
const int MAXN = 1100000 + 10;
const int MOD = 1e9 + 7;
const ll mod = 998244353; 
ll dp[100005][210][2];
ll a[maxn];
int n;

void solve() {
    cin >> n;
    for (int i = 0; i < n; ++i) {
        cin >> a[i + 1];
    }
    if (a[1] != -1) {
        dp[1][a[1]][0] = 1;
    } else {
        for (int i = 1; i < 201; ++i) {
            dp[1][i][0] = 1;
        }
    }
    for (int i = 2; i < n + 1; ++i) {
        if (a[i] == -1) {//如果是看不清的数字
            ll sum = 0;
            for (int j = 1; j < 201; ++j) {//a[i-1]<a[i]的情况，因为1是不可能比其他数字大的，所以是求前缀和
                dp[i][j][0] = sum;
                sum = (sum + dp[i - 1][j][0] + dp[i - 1][j][1]) % mod;
            }
            sum = 0;
            for (int j = 200; j > 0; --j) {//从后往前的原因是a[i-1]>=a[i]，a[i-2]必须大于a[i-1],则a[i-2]必定大于a[i],如果从前往后，那么a[i-2]是不一定大于a[i]的，有点像01背包二维变一维时的思路
                sum = (sum + dp[i - 1][j][1]) % mod;//后缀和
                dp[i][j][1] = (sum + dp[i - 1][j][0]) % mod;
            }
        } else {
            for (int j = 1; j < a[i]; ++j) {
                dp[i][a[i]][0] = (dp[i][a[i]][0] + dp[i - 1][j][0] + dp[i - 1][j][1]) % mod;
            }
            for (int j = 200; j >= a[i]; --j) {
                dp[i][a[i]][1] = (dp[i][a[i]][1] + dp[i - 1][j][1]) % mod;
            }
            //这条不要忘了
            dp[i][a[i]][1] = (dp[i][a[i]][1] + dp[i - 1][a[i]][0]) % mod;
        }
    }
    if (a[n] != -1) {//如果第n个是看得清的数字，直接输出
        cout << dp[n][a[n]][1] << endl;
    } else {//如果是看的不清的数字，将1-200之间可能的方案数相加，即为所求的答案
        ll ans = 0;
        for (int i = 1; i < 201; ++i) {
            ans = (ans + dp[n][i][1]) % mod;
        }
        cout << ans << endl;
    }
}

int main() {
    ios_base::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
#ifdef frp
    freopen("D:\\coding\\c_coding\\in.txt", "r", stdin);
//    freopen("D:\\coding\\c_coding\\out.txt", "w", stdout);
#endif
    int t = 1;
    cin >> t;
    while (t--) {
        solve();
    }
    return 0;
}