【培训题】递推的矩阵优化 contest 矩阵应用 T4 5

Description

递推是动态规划实现方法之一，因此递推在OI中十分重要。在某信息学的分支学科中，LC学会的如何求一阶线性递推数列。他想深入学习此学科，希望知道求出N阶线性递推数列。为此，他理解到以下内容：

一个k阶线性递推式是这样的式子：（见图）<br>
其中f(1),f(2)...f(k)都是已知的。<br>
也就是说，这个数列的每一项都是由他之前连续k项相加所得。其中还包括一个常数C。例如，当k=2，a1=1,a2=1,c=0时，线性递推式为：f(n)=f(n-1)+f(n-2)，这个式子就是我们熟悉的斐波那契数列。<br><br>

LC对如何去求这个式子一筹莫展，因此请你来帮助他。你的任务就是对于一个给定的k阶线性递推式，求出它的第N项f(n)mod m。

---

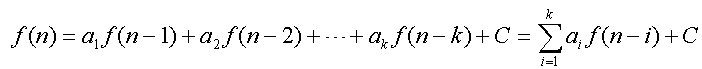
Input

输入包含多组数据。每组数据第一行为3个整数k,n,m。第二行为k个非负整数a1,a2,…,an。第三行为k个非负整数f(1),f(2),…,f(k)。输入结束标志为k=m=n=0。

---

Output

对于每组数据，输出f(n)mod m的值。

---

Hint

1<=k<=15 1<=n<=2^31-1 1<=m<=46340。

---

Solution

感觉很神奇查错查半天结果最后是错在初始化要反着初始化（因为他的系数是从大到小给的），最后mull()那个函数里面的val在赋值给anss[i]的时候忘记%了，加上去就A了，tkpl。

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define maxn 20
using namespace std;
int k,m;
long long n;
long long aa[maxn],res[maxn],a[maxn][maxn],ans[maxn][maxn],ret[maxn][maxn],anss[maxn];
inline void Mull(){
	memset(ans,0,sizeof(ans));
	for(int i=1;i<=k;i++){
		for(int j=1;j<=k;j++){
			long long val=0;
			for(int q=1;q<=k;q++){
				val+=(ret[i][q]%m*a[q][j]%m)%m;
			}
			ans[i][j]=val%m;
		}
	}
	for(int i=1;i<=k;i++){
		for(int j=1;j<=k;j++){
			ret[i][j]=ans[i][j];
		}
	}
}
inline void Mull_Self(){
	memset(ans,0,sizeof(ans));
	for(int i=1;i<=k;i++){
		for(int j=1;j<=k;j++){
			long long val=0;
			for(int q=1;q<=k;q++){
				val+=(a[i][q]%m*a[q][j]%m)%m;
			}
			ans[i][j]=val%m;
		}
	}
	for(int i=1;i<=k;i++){
		for(int j=1;j<=k;j++){
			a[i][j]=ans[i][j];
		}
	}
}
inline void Quick_Pow(long long x){
	memset(ret,0,sizeof(ret));
	for(int i=1;i<=k;i++){
		ret[i][i]=1;
	}
	while(x){
		if(x&1)Mull();
		Mull_Self();
		x>>=1;
	}
}
inline void mull(){
	for(int i=1;i<=k;i++){
		long long val=0;
		for(int j=1;j<=k;j++){
			val+=(res[k-j+1]*ret[j][i])%m;
		}
		anss[i]=val%m;
	}
}
int main(){
	while(true){
		int flag=false;
		scanf("%d%lld%d",&k,&n,&m);
		if(k==0&&n==0&&m==0)break;
		for(int i=1;i<=k;i++){
			scanf("%lld",&aa[i]);
		}
		for(int i=1;i<=k;i++){
			scanf("%lld",&res[i]);
		}
		for(int i=1;i<=k;i++){
			if(n==i){
				printf("%lld\n",res[n]);
				flag=true;
				break;
			}
		}
		if(!flag){
			memset(a,0,sizeof(a));
			for(int i=1;i<=k;i++){
				a[i][1]=aa[i];
				if(i!=k)a[i][i+1]=1;
			}
			Quick_Pow(n-k);
			mull();
			printf("%lld\n",anss[1]);
		}
	}
	return 0;
}