打鼹鼠 contest 树状数组练习 T7

Description

在一个“打鼹鼠”的游戏中，鼹鼠会不时地从洞中钻出来，不过不会从洞口钻进去（鼹鼠真胆大……）。洞口都在一个大小为n(n<=1024)的正方形中。这个正方形在一个平面直角坐标系中，左下角为(0,0)，右上角为(n-1,n-1)。洞口所在的位置都是整点，就是横纵坐标都为整数的点。而SuperBrother也不时地会想知道某一个范围的鼹鼠总数。这就是你的任务。

---

Input

第一行，一个数n，表示鼹鼠的范围。以后每一行开头都有一个数m，表示不同的操作：
m=1，x,y,k(0<=x,y<n)，表示在点(x,y)处新出现了k只鼹鼠；
m=2，x1,y1,x2,y2(0<=x1<=x2<n,0<=y1<=y2<n)，表示询问矩形(x1,y1)-(x2,y2)内的鼹鼠数量；
m=3，表示老师来了，不能玩了。保证这个数会在输入的最后一行。

---

Output

对于每个m=2，输出一行数，这行数只有一个数，即所询问的区域内鼹鼠的个数。

---

Hint

询问数不会超过10000，鼹鼠数不会超过maxlongint。n<=3000。

---

Solution

二维树状数组，维护单点修改维护一段区间和。修改和查询前缀和都很简单，跟一维都是一个思路，就是多套了一重循环，然后查询一个矩阵的和的时候,可以画个图，公式就是dofinD(xx,yy)-dofinD(x,yy)-dofinD(xx,y)+dofinD(x,y)。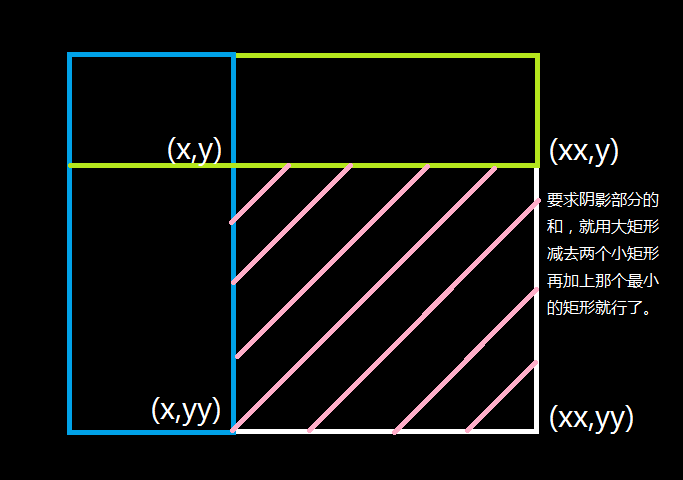

#include<cstring>
#include<cstdio>
#include<algorithm>
#include<iostream>
#define lowbit(x) (x&(-x))
#define maxn 3005
#define int long long
using namespace std;
int c[maxn][maxn];
int n,x,y,xx,yy,flag;
void doadd(int x,int y,int dd){
	while(x<=n){
		for(int i=y;i<=n;i+=lowbit(i)){
			c[x][i]+=dd;
		}
		x+=lowbit(x);
	}
}
int dofinD(int x,int y){
	int ans=0;
	while(x>0){
		for(int i=y;i>0;i-=lowbit(i)){
			ans+=c[x][i];
		}
		x-=lowbit(x);
	}
	return ans;
}
int doFind(int x,int y,int xx,int yy){
	x--,y--;
	return dofinD(xx,yy)-dofinD(x,yy)-dofinD(xx,y)+dofinD(x,y);
}
signed main(){
	scanf("%d",&n);
	while(1){
		scanf("%d",&flag);
		if(flag==3)break;
		if(flag==1){
			scanf("%d%d%d",&x,&y,&xx);
			x++,y++;
			doadd(x,y,xx);
		}
		else if(flag==2){
			scanf("%d%d%d%d",&x,&y,&xx,&yy);
			x++,y++,xx++,yy++;
			printf("%d\n",doFind(x,y,xx,yy));
		}
	}
	return 0;
}