[机器学习][K-Means] 无监督学习之K均值聚类

有监督学习虽然高效、应用范围广，但最大的问题就是需要大量的有标签的数据集，但现实生活中我们遇到的大量数据都是没有明确标签的，而且对于庞大的数据集进行标注工作本身也是一项费时费力的工作模式，所以我们希望找到一种方法能自动的挖掘数据集中各变量的关系，然后"总结"出一些规律和特征进行分类，这样的方法我们成为无监督学习(Unsupervised learning)。

在无标签的数据集中进行分类的方法成为聚类。顾名思义，聚类就是依照某种算法将相似的样本聚在一起形成一类，而不管它的标签是什么。在聚类中我们把物体所聚到的集合成为"簇"(cluster)。目前常用的无监督学习方法有K均值聚类、基于密度聚类、主成分分析法、等等，其中K均值聚类是常用的经典方法，而主成分分析法是经典的数据降维方法，我们本节着重介绍一下K均值聚类和主成分分析法。

 

K均值聚类

    在K均值(K-means)聚类中，K代表了簇的数量，也就是分类个数。均值是该算法聚类的核心思想。K均值算法是以簇内最小均方误差来作为损失函数，假设我们将样本集分为K个簇，第i个簇记为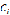，则损失函数可被写为：

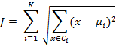
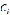其中为簇内的平均值，这也是K均值算法中均值所代表的的意义。这个损失函数刻画了簇内样本围绕均值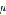的紧密程度，也就是簇内样本的相似程度。K均值算法聚类流程如下：

1. 在样本集中随机选取K个样本点作为均值的初始值
2. 计算每个样本和每个均值点之间的距离
3. 将样本划入距离最近的均值点所在的簇
4. 根据簇内样本更新每个均值点。
5. 重复步骤2-4
6. 得到K个簇。

    下面我们依然用一个例子对K均值算法的聚类过程进行说明。我们分别围绕坐标平面内的点和点各生成100个具有标准差为1的高斯白噪声的样本，如图12左上角的图所示。我们用K均值算法对这个样本集进行聚类，理想情况下K均值算法能仅通过这些样本找到我们的初始样本中心点和。对样本集进行四轮迭代，每次迭代的聚类情况如图12所示。

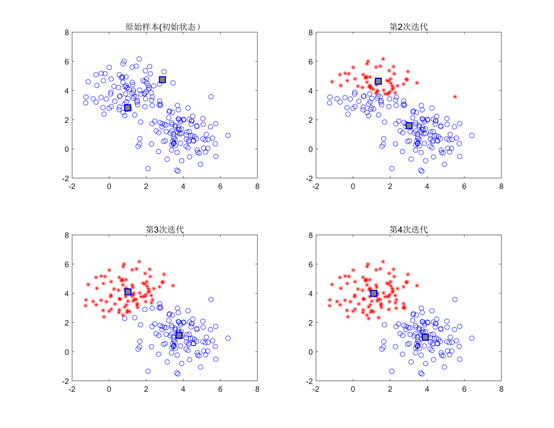
图12 K均值算法迭代更新过程

    图12中每个簇的均值点用灰色方块表示，可以看到，尽管一开始初始状态时两个均值点是随机选取的，但随着迭代的进行，最终这两个均值点会移动到一个最佳位置使这两个簇尽量远，这个例子中当进行了4次迭代后两个簇的均值点的坐标分别是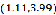和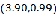,可以看出已经非常接近我们生成样本时所用的中心点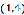和，说明聚类效果非常好。

    当然，上面例子我们用的是K=2的情况，也就是将数据集分为了两类，但现实中有很多问题我们事先并不知道有几类，那么我们可以尝试不同K值，得到一个满意的效果。图13展示了对上面提到的样本集进行K=2,K=3,K=4的K均值聚类。

图13 不同K的取值下K均值聚类效果