HanLP — HMM隐马尔可夫模型 -- 训练

BMES => B-begin:词语开始、M-middle：词语中间、E-end：词语结束、S-single:单独成词

训练的过程，就是求三个矩阵的过程

• 初始概率矩阵
• 转移概率矩阵
• 发射概率矩阵

每个字有4种可能性，上图中有7个字，就是 4^7 种可能性

维特比算法，从众多路径中，挑出最优的那条，他和隐马尔可夫没有强关联

初始概率矩阵

今天 天气 真 不错。 麻辣肥牛 好吃 ！ 我 喜欢 吃 好吃 的！

=>

BE BE S BE S (标点也是一个独立的S) BMME BE S S BE S BE S S

统计每篇文章（每行）第一个字是什么状态（统计的数值都是频次）

B	M	S	E
2	0	1	0

如果 M、E 有值，那代码 100% 是写错了，因为 第一个字，不可能是中间，也不可能是结束

根据频率得到概率

B	M	S	E
0.667	0	0.333	0

2/3 = 0.667
1/3 = 0.333

转移概率矩阵

当前状态到下一状态的概率

一次循环搞定

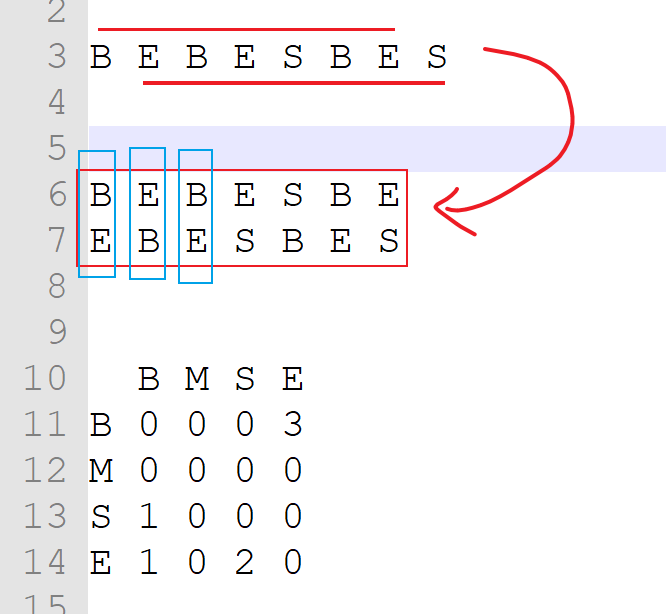
按行统计 BM = 1/(1+6) = 0.142 , 6/7 = 0.857

发射概率矩阵

统计某种状态下，所有字出现的次数（概率）

依次遍历语料库的每一个字

train_data.txt

今天 天气 真 不错 。
麻辣肥牛 好吃 ！
我 喜欢 吃 好吃 的 ！

train_state.txt

BE BE S BE S
BMME BE S
S BE S BE S S

# 训练数据
[
  '今天 天气 真 不错 。',
  '麻辣肥牛 好吃 ！',
  '我 喜欢 吃 好吃 的 ！'
]
# 标注
[
  'BE BE S BE S',
  'BMME BE S',
  'S BE S BE S S '
]

# 初始矩阵
[2, 0, 1, 0]

# 转移矩阵
[
  [0, 1, 0, 6],
  [0, 1, 0, 1],
  [3, 0, 1, 0],
  [2, 0, 5, 0]
]

# 发射矩阵
{
  'B': {'total': 7, '今': 1, '天': 1, '不': 1, '麻': 1, '好': 2, '喜': 1},
  'M': {'total': 2, '辣': 1, '肥': 1},
  'S': {'total': 7, '真': 1, '。': 1, '！': 2, '我': 1, '吃': 1, '的': 1},
  'E': {'total': 7, '天': 1, '气': 1, '错': 1, '牛': 1, '吃': 2, '欢': 1}
}

源代码

import pickle
from tqdm import tqdm
import numpy as np
import os


def make_label(text_str):
    """从单词到label的转换, 如: 今天 ----> BE  麻辣肥牛: ---> BMME  的 ---> S"""
    text_len = len(text_str)
    if text_len == 1:
        return "S"
    return "B" + "M" * (text_len - 2) + "E"  # 除了开头是 B, 结尾是 E，中间都是Ｍ


def text_to_state(train_file, state_file):
    """ 将原始的语料库转换为 对应的状态文件 """
    if os.path.exists(state_file):  # 如果存在该文件, 就直接退出
        os.remove(state_file)
    # 打开文件并按行切分到  all_data 中 , all_data  是一个list
    all_data = open(train_file, "r", encoding="utf-8").read().split("\n")
    with open(state_file, "w", encoding="utf-8") as f:  # 代开写入的文件
        for d_index, data in tqdm(enumerate(all_data)):  # 逐行 遍历 , tqdm 是进度条提示 , data 是一篇文章, 有可能为空
            if data:  # 如果 data 不为空
                state_ = ""
                for w in data.split(" "):  # 当前 文章按照空格切分, w是文章中的一个词语
                    if w:  # 如果 w 不为空
                        state_ = state_ + make_label(w) + " "  # 制作单个词语的label
                if d_index != len(all_data) - 1:  # 最后一行不要加 "\n" 其他行都加 "\n"
                    state_ = state_.strip() + "\n"  # 每一行都去掉 最后的空格
                f.write(state_)


# 定义 HMM类, 其实最关键的就是三大矩阵
class HMM:
    def __init__(self, file_text, file_state):
        self.all_states = open(file_state, "r", encoding="utf-8").read().split("\n")[:200]  # 按行获取所有的状态
        self.all_texts = open(file_text, "r", encoding="utf-8").read().split("\n")[:200]  # 按行获取所有的文本
        self.states_to_index = {"B": 0, "M": 1, "S": 2, "E": 3}  # 给每个状态定义一个索引, 以后可以根据状态获取索引
        self.index_to_states = ["B", "M", "S", "E"]  # 根据索引获取对应状态
        self.len_states = len(self.states_to_index)  # 状态长度 : 这里是4

        # 初始概率矩阵 : 1 * 4 , 对应的是 BMSE,
        self.init_matrix = np.zeros((self.len_states))
        # 转移概率矩阵:  4 * 4 ,
        self.transfer_matrix = np.zeros((self.len_states, self.len_states))

        # 发射概率矩阵, 使用的 2级 字典嵌套，
        # # 注意这里初始化了一个  total 键 , 存储当前状态出现的总次数, 为了后面的归一化使用
        self.emit_matrix = {"B": {"total": 0}, "M": {"total": 0}, "S": {"total": 0}, "E": {"total": 0}}

    # 计算 初始概率矩阵，统计每行第一个字出现的频次
    def cal_init_matrix(self, state):
        self.init_matrix[self.states_to_index[state[0]]] += 1  # BMSE 四种状态, 对应状态出现 1次 就 +1

    # 计算 转移概率矩阵，当前状态到下一状态的概率
    def cal_transfer_matrix(self, states):
        sta_join = "".join(states)  # 状态转移 从当前状态转移到后一状态, 即 从 sta1 每一元素转移到 sta2 中
        sta1 = sta_join[:-1]
        sta2 = sta_join[1:]
        for s1, s2 in zip(sta1, sta2):  # 同时遍历 s1 , s2  -- (('B', 'E'), ('E', 'B'), ('B', 'E'), ('E', 'S'), ('S', 'B'), ('B', 'E'), ('E', 'S'))
            self.transfer_matrix[self.states_to_index[s1], self.states_to_index[s2]] += 1

    # 计算 发射矩阵，在特定状态下，出现某个字的概率
    def cal_emit_matrix(self, words, states):
        """计算 发射矩阵，在特定状态下，出现某个字的概率
        [
          '今天 天气 真 不错 。',
          '麻辣肥牛 好吃 ！',
          '我 喜欢 吃 好吃 的 ！'
        ]
        [
          'BE BE S BE S',
          'BMME BE S',
          'S BE S BE S S '
        ]
        {
          'B': {'total': 7, '今': 1, '天': 1, '不': 1, '麻': 1, '好': 2, '喜': 1},
          'M': {'total': 2, '辣': 1, '肥': 1},
          'S': {'total': 7, '真': 1, '。': 1, '！': 2, '我': 1, '吃': 1, '的': 1},
          'E': {'total': 7, '天': 1, '气': 1, '错': 1, '牛': 1, '吃': 2, '欢': 1}
        }
        """
        print(tuple(zip("".join(words), "".join(states))))
        for word, state in zip("".join(words), "".join(states)):  # 先把words 和 states 拼接起来再遍历, 因为中间有空格
            self.emit_matrix[state][word] = self.emit_matrix[state].get(word, 0) + 1
            self.emit_matrix[state]["total"] += 1  # 注意这里多添加了一个  total 键 , 存储当前状态出现的总次数, 为了后面的归一化使用

    # 训练开始, 其实就是3个矩阵的求解过程
    def train(self):
        for words, states in tqdm(zip(self.all_texts, self.all_states)):  # 按行读取文件, 调用3个矩阵的求解函数
            words = words.split(" ")  # 在文件中 都是按照空格切分的
            states = states.split(" ")
            self.cal_init_matrix(states[0])  # 初始矩阵，统计每行第一个字出现的频次 [2. 0. 1. 0.]
            self.cal_transfer_matrix(states) # 转移矩阵，当前状态到下一状态的概率
            self.cal_emit_matrix(words, states)  # 发射矩阵，在特定状态下，出现某个字的概率


if __name__ == "__main__":
    train_file = "data/train_data.txt"
    state_file = "data/train_state.txt"
    text_to_state(train_file, state_file)
    hmm = HMM(train_file, state_file)
    hmm.train()

源码：https://gitee.com/VipSoft/VipPython/tree/master/hmm_viterbi

视频：https://www.bilibili.com/video/BV1aP4y147gA?p=4