python解决组合问题
1.问题描述
比如9个数中取4个数的组合以及列出各种组合,该如何做?
我们可以考虑以下一个简单组合:从1,2,3,4,5,6中,如何选取任意四个数的组合。
固定:1 2 3 ,组合有1234 1235 1236
固定1 2 4,组合有:1245 1246
固定1 2 5,组合有:1256
固定1 3 4,组合有:1345 1346
固定1 3 5,组合有:1356
固定1 4 5,组合有:1456
固定2 3 4,组合有:2345 2346
固定2 3 5,组合有:2356
固定2 4 5,组合有:2456
固定3 4 5,组合有:3456
共有15种组合
2.简单实现一下组合算法
首先,我们分析上面列出的10个步骤,对于1),很明显,在固定了1 2 3这三个数之后,第四个数就是4、5、6三个数进行了循环(还记得循环吗,计算机最拿手的就是做循环)。其次,我们再分析1)2)3)这三个步骤中固定的数字,前两个没有变,都是1 2,只是第三个数在进行循环(又是循环)。
通过分析,我们可以找到这样的规律:
1 先固定3个数,让第四个数进行循环
2 让第三个数循环,重复第一步
3 让第二个数循环,重复第一步
4 让第一个数循环,重复第一步
def combNumberLoop4(m, b): totalNumber = 0 for i in range(1, m+2-4): b[0] = i for j in range(i+1, m+2-3): b[1] = j for k in range(j+1, m+2-2): b[2] = k for l in range(k+1, m+2-1): b[3] = l print b totalNumber += 1 return totalNumber group=[99,99,99,99] print "\nUsing Loop: %d\n" % combNumberLoop4(6, group)
程序的输出结果,正如之前分析的那样。
3.如何递归解决组合问题
我们再回到C(6,4)问题,除了上面列出的十个步骤,我们换个思路:
如果在6个数中选定一个数,那么确定剩下的3个数是不是变为了“从5个数中选3个数的组合问题”了呢?以此类推,这似乎变成了一个“递归”问题了,确实,我们可以用递归的思路来解决这个问题。
对于C(m, n)列出所有组合的问题,可以按照一下的步骤来进行编程,这次我们按从后往前的顺序来列出所有组合:
1 选定一个元素i,在范围[m, n]内进行循环
2 将i 作为所求组合的最后一个元素
3 如果n-1>0,进行递归调用,求C(m-1, n-1);否则,输出结果
4 重复①
注意,设计递归函数一定要有终止条件,否则会造成“死循环”。
实现的代码如下:
def combNumber(m, n, b): global totalNumberR for i in range(m, n-1, -1): b[n-1] = i if n-1>0: combNumber(i-1,n-1,b) else: print b totalNumberR += 1 return totalNumberR group=[99,99,99,99,99] totalNumberR = 0 print "\nUsing Recursive: %d\n" % combNumber(7,5,group)
递归的使用,让程序写起来非常的简洁,但是,在写程序的时候,我有两个地方(其实程序也就难在这两个地方),折腾了好几天才弄清楚:
首先是for循环的循环范围如何确定;
其次是递归调用时使用的参数设计;
3.python提供的内置组合函数
def combinations_with_replacement(iterable, r): # combinations_with_replacement('ABC', 2) --> AA AB AC BB BC CC pool = tuple(iterable) n = len(pool) if not n and r: return indices = [0] * r yield tuple(pool[i] for i in indices) while True: for i in reversed(range(r)): if indices[i] != n - 1: break else: return indices[i:] = [indices[i] + 1] * (r - i) yield tuple(pool[i] for i in indices)
4.更多组合算法
请点击我:https://docs.python.org/3/library/itertools.html?highlight=combinations#itertools.combinations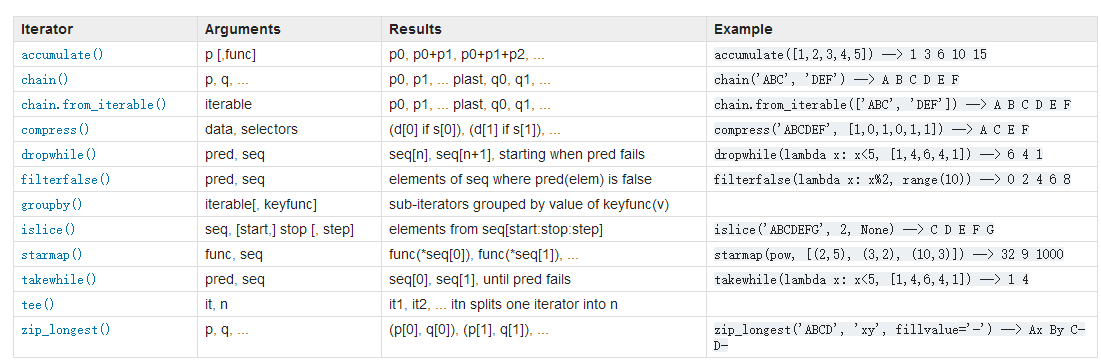


 浙公网安备 33010602011771号
浙公网安备 33010602011771号