八大排序算法之希尔排序

描述

　　希尔排序(Shell Sort)是插入排序的一种。也称缩小增量排序，是直接插入排序算法的一种更高效的改进版本。希尔排序是非稳定排序算法。该方法因DL．Shell于1959年提出而得名。 希尔排序是把记录按下标的一定增量分组，对每组使用直接插入排序算法排序；随着增量逐渐减少，每组包含的关键词越来越多，当增量减至1时，整个文件恰被分成一组，算法便终止。

设计思想:　　

　　把记录按步长 gap 分组，对每组记录采用直接插入排序方法进行排序。随着步长逐渐减小，所分成的组包含的记录越来越多，当步长的值减小到 1 时，整个数据合成为一组，构成一组有序记录，则完成排序。

图示

　

 

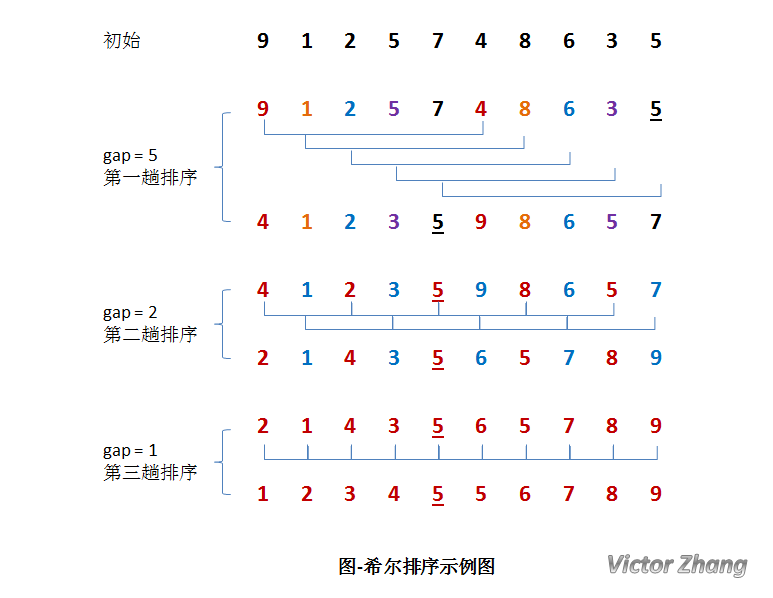
分析　

　　初始时，有一个大小为 10 的无序序列。

　　在第一趟排序中，我们不妨设 gap1 = N / 2 = 5，即相隔距离为 5 的元素组成一组，可以分为 5 组。

　　接下来，按照直接插入排序的方法对每个组进行排序。

　　在第二趟排序中，我们把上次的 gap 缩小一半，即 gap2 = gap1 / 2 = 2 (取整数)。这样每相隔距离为 2 的元素组成一组，可以分为 2 组。

　　按照直接插入排序的方法对每个组进行排序。

　　在第三趟排序中，再次把 gap 缩小一半，即gap3 = gap2 / 2 = 1。 这样相隔距离为 1 的元素组成一组，即只有一组。

　　按照直接插入排序的方法对每个组进行排序。此时，排序已经结束。

　　需要注意一下的是，图中有两个相等数值的元素 5 和 5 。我们可以清楚的看到，在排序过程中，两个元素位置交换了。

　　所以，希尔排序是不稳定的算法。

代码实现

def get_number(num):
    import random
    lst = []
    i = 0
    while i < num:
        lst.append(random.randint(0,100))
        i += 1
    return lst

def shellsort(lst):
    count = len(lst)
    step = 2  # 起始步长
    group = count // step  # 根据步长进行分组排序
    while group > 0:
        for i in range(0,group):
            j = i + group
            while j < count:
                k = j - group
                key = lst[j]
                while k >= 0:
                    if lst[k] > key:
                        lst[k+group] = lst[k]
                        lst[k] = key
                    k -= group
                j += group
        group //= step  # 取整数部分

    return lst

a = get_number(10)
print("排序之前:",a)
b = shellsort(a)
print("排序之后:",b)

####输出结果#########
排序之前: [71, 34, 15, 66, 36, 40, 2, 58, 33, 77]
排序之后: [2, 15, 33, 34, 36, 40, 58, 66, 71, 77]

性能分析

　　算法稳定性:由上文的希尔排序算法演示图即可知，希尔排序中相等数据可能会交换位置，所以希尔排序是不稳定的算法。

　　平均时间复杂度：O(Nlog2N)

　　空间复杂度:O(1)

排序效果