八大排序算法之堆排序
堆的介绍
堆是一棵顺序存储的完全二叉树。
其中每个结点的关键字都不大于其孩子结点的关键字,这样的堆称为小根堆。
其中每个结点的关键字都不小于其孩子结点的关键字,这样的堆称为大根堆。
举例来说,对于n个元素的序列{R0, R1, ... , Rn}当且仅当满足下列关系之一时,称之为堆:
(1) Ri <= R2i+1 且 Ri <= R2i+2 (小根堆)
(2) Ri >= R2i+1 且 Ri >= R2i+2 (大根堆)
算法思想:
根据初始数组去构造初始堆(构建一个完全二叉树,保证所有的父结点都比它的孩子结点数值大)。
每次交换第一个和最后一个元素,输出最后一个元素(最大值),然后把剩下元素重新调整为大根堆。
代码实现:
def get_number(num): import random lst = [] i = 0 while i < num: lst.append(random.randint(0,100)) i += 1 return lst def adjust_heap(lst,i,size): #调整堆结构 lchild = 2 * i + 1 # 左孩子 rchild = 2 * i + 2 # 右孩子 max = i # 假设当前为最大 if i < size // 2: if lchild < size and lst[lchild] > lst[max]: max = lchild if rchild < size and lst[rchild] > lst[max]: max = rchild if max != i: lst[max],lst[i] = lst[i],lst[max] adjust_heap(lst,max,size) def build_heap(lst,size): # 构造堆 for i in range(0,(size // 2))[::-1]: adjust_heap(lst,i,size) def heapsort(lst): size = len(lst) build_heap(lst,size) for i in range(0,size)[::-1]: lst[0],lst[i] = lst[i],lst[0] adjust_heap(lst,0,i) return lst a = get_number(10) print("排序之前:",a) b = heapsort(a) print("排序之后:",b) ##输出结果###### 排序之前: [31, 91, 77, 45, 62, 62, 78, 36, 34, 25] 排序之后: [25, 31, 34, 36, 45, 62, 62, 77, 78, 91]
性能分析:
时间复杂度
堆的存储表示是顺序的。因为堆所对应的二叉树为完全二叉树,而完全二叉树通常采用顺序存储方式。
当想得到一个序列中第k个最小的元素之前的部分排序序列,最好采用堆排序。
因为堆排序的时间复杂度是O(n+klog2n),若k≤n/log2n,则可得到的时间复杂度为O(n)。
空间复杂度
O(1)
算法稳定性
堆排序是一种不稳定的排序方法。
因为在堆的调整过程中,关键字进行比较和交换所走的是该结点到叶子结点的一条路径,
因此对于相同的关键字就可能出现排在后面的关键字被交换到前面来的情况。
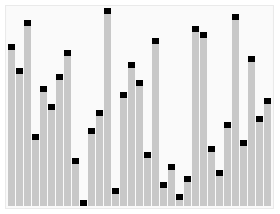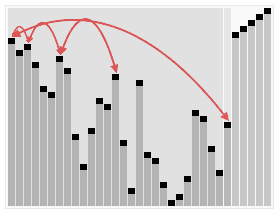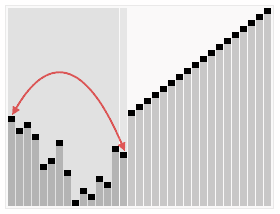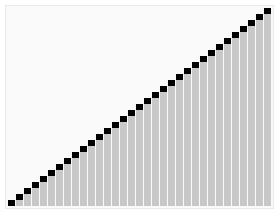
排序效果


 浙公网安备 33010602011771号
浙公网安备 33010602011771号