八大排序算法之快速排序

  算法思想：快速排序运用了分而治之的思想，即在所选数组中选择一个基准(任选一个都可以)，以改基准为基础，将小于该基准的元素都移动基准的左边，大于该基准的数据都移动到右边，然后对左右两边进行递归处理。同样也是按照上述方法，即：选基准，在递归。                                                          

代码实现：

def get_number(num):
    import random
    lst = []
    i = 0
    while i < num:
        lst.append(random.randint(0,100))
        i += 1
    return lst

def quicksort(lst):  
    if len(lst) < 2:
        return lst
    else:
        pivot = lst[0]
        greater,less = [],[]
        for i in lst[1:]:
            if i <= pivot:
                less.append(i)
            else:
                greater.append(i)
    return quicksort(less) + [pivot] + quicksort(greater)

a = get_number(10)
print("排序之前:",a)
b = quicksort(a)
print("排序之后:",b)

#####结果#######
排序之前: [76, 62, 92, 43, 61, 77, 41, 62, 1, 10]
排序之后: [1, 10, 41, 43, 61, 62, 62, 76, 77, 92]

 

算法性能分析：

　　　　最坏情况下，时间复杂度为O(n^2)

　　　　在这种情况下，我们来看看一个极端的例子 A = [1,2,3,4,5,6,7,8,9]这个序列原本就是有序的，如果我们选取元素1作为基准，对其进行调用快速排序，其调用递归栈的长度为n。但是如果我们选取中间元素5作为基准，其调用递归栈长度为logn。

　　　　平均情况下，时间复杂度为O(nlogn)

在快速排序中有两个关键点：

　　第一，递归出口的判断

　　　　　对于递归出口，我们可以来考虑几种特殊情况：

　　　　　当数组中没有元素时，这时应该直接返回就行；当数组中只有一个元素的时候，也应该和直接返回。因此，当数组中元素为空或者仅有一个元素的时候，程序就应该返回。

　　第二，递归表达式的确定

　　　　　对于快速排序，从其算法思想来考虑，应该是这样的。

　　　　    [小于基准]   +    [基准]     +     [大于基准]

　　　　　我们清楚了这一点之后，然后分别对小于基准部分和大于基准部分都来调用快速排序。这样我们就可以得到快排递归表达式。

　　　　　quicksort(less_part)  + [基准]  +  quicksort(great_part)

　　　　

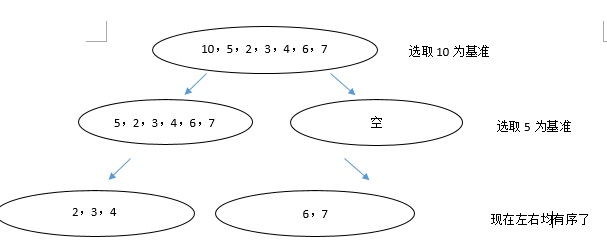
     快速排序的中间过程，其实就是一棵递归树。当递归到达叶子节点，这时递归也就结束了，程序就执行完毕了。

　排序效果：