CSP-S 2022 数据传输
[CSP-S 2022] 数据传输
思路
对于 \(20\%\) 的数据
直接暴力,期望得分 20。
对于 \(44\%\) 的数据
预处理所有可以相互到达的点对,边权为两个点的点权和,原问题变为最短路,令最短路长度为 \(v\) 答案为 \(\frac{v+a_s+a_t}{2}\) 时间复杂度 \(O(n^2+qn\log n)\)。
对于 \(k=1\) 的情况
可以发现数据一定按照 \(s\to t\) 的链传输,所以只需要求树上链和,树上差分即可。
对于 \(k=2\) 的情况
我们进一步分析。考虑当 \(k=2\) 时走出 \(s\to t\) 的链是没有意义的,考虑走出链两步还不如不走,而向根走一次在向外走一次,那么第二次必须先走回去在向上走一次,不如直接一步向上跳两条边。
那么直接把询问的链拎出来,在链上 \(dp\),设 \(dp_{i}\) 表示从 \(s\) 走到 \(i\) 的最小权和,那么有转移 \(dp_{i}=\min (dp_{i-1},dp_{i-2})+a_i\),结合数据随机树高 \(\log\) 的部分分。至此已经可以获得 64 分。
我们考虑用矩阵+倍增/树剖优化 \(dp\) 的过程,设 \(dp_{u,i}\) 表示从 \(u\) 往上跳 \(2^i\) 条边的最小代价,对于每个 \(dp\) 设计一个 \(2\times 2\) 的矩阵,其中 \(m_{j,k}\) 表示钦定起点距离链首的距离为 \(j\),最终达到的位置距离链的终点的距离为 \(k\)。
考虑对每个点预处理 \(dp_{u,0,0,0}=a_u+a_{fa_u},dp_{u,0,0,1}=a_u,dp_{u,0,1,0}=a_{fa_u}\) 转移等价于矩阵乘法的转移,另 \(c_{i,j}=\min_{k\in{0,1}} a_{i,k}+b_{k,j}\) 。特别的,当 \(k=0\) 时两条链相交的点的贡献会算重,所以转移的时候需要减 \(!k?a_{mid}:0\)。
考虑处理询问,先让 \(s,t\) 分别跳到 \(lca(s,t)\),倍增处理两个矩阵,那么答案为 \(\min(a_{0,1}+b_{0,1},a_{0,0}+b_{0,0}-a_{lca})\)。
至此已经可以获得 76 分。
对于 \(k=3\) 的情况
考虑正解。
根据 \(k=2\) 的性质我们进一步发现,\(k=3\) 时最多只会跳出链一条边,因为每次跳不管到哪,必须保证当前跳到的位置的深度小于没跳之前的深度,这样的跳可以总结为三种情况。
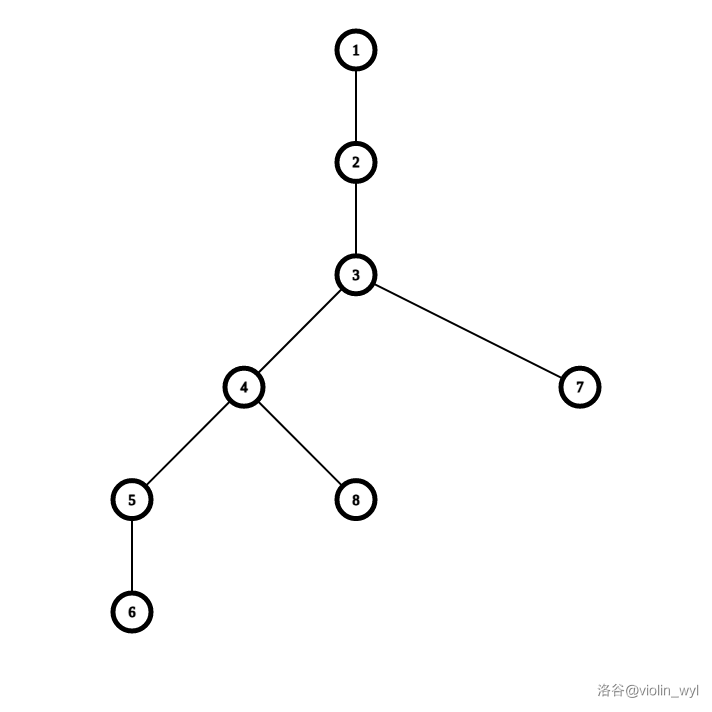
如果我们从 \(6\to 1\),可以从 \(6\to 8,8\to 7,7\to 1\)。不难证明只有这三种出链的情况。
考虑扩展矩阵,下标为 \(2\) 则距离为 2,下标为 \(3\) 则是表示当前是否出链(默认且必须与起点/终点距离为1)。
预处理的东西比较多,具体可以看代码。
最终处理答案的细节较多,注意可以走到 \(lca\),所以答案包括 \(a_{0,2}+a_{fa_{lca}}+b_{0,2}\)。
code
代码中矩阵在 \((1,0),(2,0)\) 与题解中略有不同,以代码为准。
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N = 2e5 + 10;
typedef pair <int, int> pii;
inline int read ()
{
int x = 0, f = 1;
char c = getchar ();
while (c < '0' || c > '9') { if (c == '-') f = -1; c = getchar (); }
while (c >= '0' && c <= '9') { x = (x << 1) + (x << 3) + (c ^ 48); c = getchar (); }
return x * f;
}
int n, q, d;
int val[N], mn[N];
struct edge {
int ver, nxt;
} e[N << 1];
int head[N], tot;
void add_edge (int u, int v) { e[++tot] = (edge) {v, head[u]}; head[u] = tot; }
int fa[N][20], f[N], depth[N], lg[N];
struct Matrix {
int a[4][4];
} dp[N][20], t;
int tmp;
Matrix operator + (const Matrix &a, const Matrix &b)
{
Matrix c;
memset (c.a, 0x3f, sizeof(c.a));
for (int i = 0; i < d; i++)
for (int j = 0; j < d; j++)
for (int k = 0; k < d; k++)
{
int del = 0;
if (k == 0) del = val[tmp];
if (k == 3) del = mn[tmp];
c.a[i][j] = min (c.a[i][j], a.a[i][k] + b.a[k][j] - del);
}
return c;
}
void Min (Matrix &a, Matrix &b)
{
for (int i = 0; i < d; i++)
for (int j = 0; j < d; j++)
for (int k = 0; k < d; k++)
a.a[i][j] = min (a.a[i][j], b.a[i][j]);
}
void dfs (int u, int Fa)
{
f[u] = fa[u][0] = Fa; depth[u] = depth[Fa] + 1;
for (int i = 1; i <= lg[depth[u]]; i++) fa[u][i] = fa[fa[u][i - 1]][i - 1];
for (int i = head[u]; i; i = e[i].nxt)
{
int v = e[i].ver;
if (v == Fa) continue;
mn[u] = min (mn[u], val[v]);
}
dp[u][0].a[0][0] = val[u] + val[f[u]];
if (d == 2)
{
dp[u][0].a[0][1] = val[u];
dp[u][0].a[1][0] = val[f[u]];
}
if (d == 4)
{
dp[u][0].a[1][0] = val[f[u]];
dp[u][0].a[0][1] = val[u];
dp[u][0].a[2][0] = val[f[u]];
dp[u][1].a[1][0] = val[f[f[u]]];
dp[u][1].a[0][2] = val[u];
dp[u][0].a[1][2] = 0;
dp[u][0].a[0][3] = val[u] + mn[f[u]];
dp[u][0].a[3][3] = mn[u] + mn[f[u]];
dp[u][0].a[3][0] = val[f[u]] + mn[u];
dp[u][0].a[1][3] = mn[f[u]];
dp[u][0].a[3][2] = mn[u];
dp[u][1].a[0][3] = val[u] + mn[f[f[u]]];
dp[u][1].a[3][0] = val[f[f[u]]] + mn[u];
}
for (int i = 1; i <= lg[depth[u]]; i++)
{
tmp = fa[u][i - 1];
if (i == 1) Min (dp[u][i], (t = dp[u][i - 1] + dp[fa[u][i - 1]][i - 1]));
else dp[u][i] = dp[u][i - 1] + dp[fa[u][i - 1]][i - 1];
}
for (int i = head[u]; i; i = e[i].nxt)
{
int v = e[i].ver;
if (v == Fa) continue;
dfs (v, u);
}
}
int getlca (int x, int y)
{
if (depth[x] < depth[y]) swap (x, y);
while (depth[x] > depth[y]) x = fa[x][lg[depth[x] - depth[y]] - 1];
if (x == y) return x;
for (int i = lg[depth[x]]; i >= 0; i--)
if (fa[x][i] != fa[y][i]) x = fa[x][i], y = fa[y][i];
return fa[x][0];
}
Matrix find (int now, int len)
{
Matrix res; bool flag = 0;
memset (res.a, 0, sizeof (res.a));
for (int i = lg[depth[now]]; i >= 0 && now && len; i--)
{
if (len >= (1 << i))
{
tmp = now;
if (flag) res = res + dp[now][i];
else
{
flag = true;
for (int j = 0; j < d; j++)
for (int k = 0; k < d; k++) res.a[j][k] = dp[now][i].a[j][k];
}
len -= (1 << i);
now = fa[now][i];
}
}
return res;
}
signed main ()
{
n = read (), q = read (), d = read (); if (d == 3) d++;
for (int i = 1; i <= n; i++) val[i] = read ();
for (int i = 1; i < n; i++)
{
int u = read (), v = read ();
add_edge (u, v);
add_edge (v, u);
}
for (int i = 1; i <= n; i++) lg[i] = lg[i - 1] + (1 << lg[i - 1] == i);
memset (dp, 0x3f, sizeof (dp));
memset (mn, 0x3f, sizeof (mn));
dfs (1, 0);
while (q--)
{
int s = read (), t = read ();
int lca = getlca (s, t);
if (s == t) printf ("%lld\n", val[s]);
else if (lca == s || lca == t)
{
if (depth[s] < depth[t]) swap (s, t);
Matrix a = find(s, depth[s] - depth[t]);
printf ("%lld\n", a.a[0][0]);
}
else
{
Matrix a = find(s, depth[s] - depth[lca]);
Matrix b = find(t, depth[t] - depth[lca]);
int ans = a.a[0][0] + b.a[0][0] - val[lca];
if (d >= 2) ans = min (ans, a.a[0][1] + b.a[0][1]);
if (d >= 3)
{
int mn1 = a.a[0][3] + b.a[0][3] - mn[lca];
if (lca != 1) mn1 = min (mn1, a.a[0][2] + val[f[lca]] + b.a[0][2]);
int mn2 = min (a.a[0][2] + b.a[0][1], a.a[0][1] + b.a[0][2]);
ans = min (ans, min (mn1, mn2));
}
printf ("%lld\n", ans);
}
}
return 0;
}
