CF1080D Solution

题目链接

题解

可以发现，为了左下到右上经过的方格边长相等，要么将左下右上曼哈顿距离上的方格全部分割，要么避开全部曼哈顿距离上的方格。

此段为下段的证明，如果节约脑细胞且只希望感性理解的读者可以略过 (¬‿¬) → 暂且忽略边长，并只考虑在同一边长的小正方形中分割。设大正方形边由\(m\)个小正方形组成，在其中分割的次数为\(k'\)。依照上述经过边长相等的条件，也就是\(k'\le m^2-(2m-1)\) —①或\(k'\ge 2m-1\) —②。易得\(m^2-2m+1\ge 2m+1\)时，该不等式组一定有解，化简后得\(m\ge 4\)。所以当一个大正方形的\(m<4\)，且分割出的小正方形无法继续分割时，存在无可行路径的分割数。又因为\(m\)一定是\(2\)的若干次幂，所以只有\(m=2/1\)时才会出现上述情况。将\(m=2\)代入①②，解得\(k'\le 1\)或\(k'\ge 3\)；将\(m=1\)代入①②，解得\(k'\le 0\)或\(k'\ge 1\)，也就是只有\(k'=2\)时无解。

总结一下，只有\(n=2,k=3\)时会出现\(m=2,k'=2\)（也就是无可行路径）的情况，如右图（当然还有其他分割方法，但是它们也都不可行）：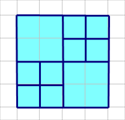

除了上述情况以外，当已经无法分割但是\(k\)仍有剩余（如样例的测试数据3）时也不可行。

如何计算经过的方格长度呢？我们将每一组边长相等且有\(4^i\)个的小正方形称为一层，如上图，第1层是\(4\)个边长为\(2\)的小正方形，第2层是\(16\)个边长为\(1\)的小正方形。循环累加\(4^i\)至\(k\)为止，在判断多出的分割数是否大于曼哈顿距离即可确定路径中方格的层数。每一层小正方形的边长\(log2=n-\)层数（容易推出，请读者自行证明 (。﹏。)）。

AC代码

#include<bits/stdc++.h>
#define int long long
using namespace std;
signed main()
{
	int t,n,k;
	scanf("%lld",&t);
	while(t--)
	{
		scanf("%lld%lld",&n,&k);
		if(n==2 && k==3) {printf("NO\n"); continue;}
		int qwq=4,ans=1,cnt=1;//qwq:4的ans次方,ans:路径所在层数,cnt:分割前ans层所需次数
		while(cnt<=k)
		{
			cnt+=qwq; qwq*=4;
			ans++;
		}
		ans--; qwq/=4; cnt-=qwq;
		if(ans>n || (ans==n && k>cnt)) {printf("NO\n"); continue;}//k大于可分割的最大数量
		if(k-cnt>=2*(1<<ans)-1) ans++;//经过曼哈顿距离
		printf("YES %d\n",n-ans);
	}
	return 0;
}