CF509E Pretty Song 题解

看到这题要求每个子串对答案的贡献，于是想到了 SAM。写了一个 SAM 后才发现复杂度有大问题（

子串不好处理，我们可以想想字母 I,E,A,O,U,Y 对每个子串的贡献。

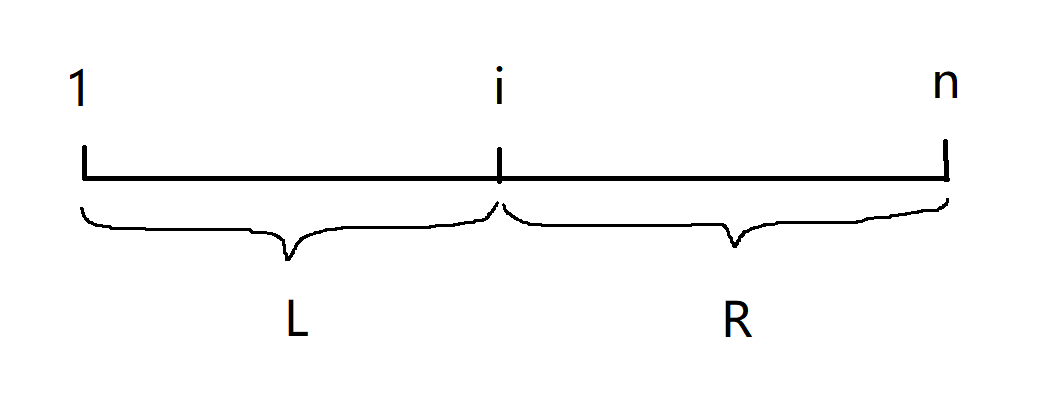
如图，我们假设现在在第 \(i\) 个字母，它是一个特殊字母（例如 I）。包含它的子串就是在 \([1,i]\) 和 \([i,n]\) 各选取一个端点组成的子串。

我们先考虑模拟这个过程。

枚举每个左端点，看左右端点组成的子串的长度范围。

\([1,r],[2,r-1],[3,r-2]...,[l-1,l+r-2],[l,l+r-1]\)

我们可以发现可以通过统计对答案有贡献的子串长度个数，最后答案就是 \(\sum_{i=1}^{n}c[i]/i\)。

但是这个复杂度是 \(O(n^2)\) 的，依然无法通过此题。

考虑观察差分过程。

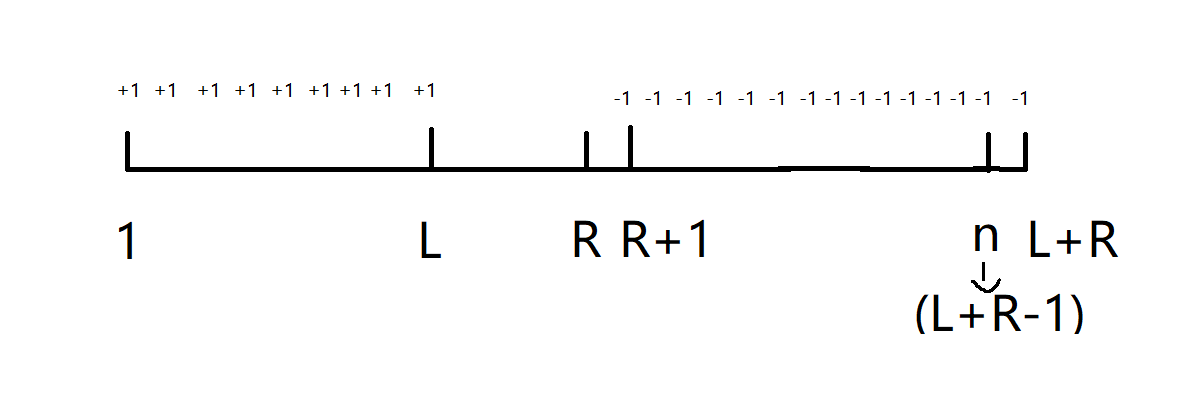
可以发现，+1 是连续的一段，-1 也是连续的一段，于是我们可以再来一次差分。

最后这个字母对二次差分数组的影响就是：

c[1]++;c[l+1]--;c[r+1]--;c[l+r]++;

统计完每个字母对答案的贡献最后还原原来的统计数组就行了。

代码：

#include<bits/stdc++.h>
#define pc(x) putchar(x)
#define int long long
#define dl double
using namespace std;
inline int read()
{
    int x=0,f=1;char ch=getchar();
    while(ch<'0'||ch>'9'){f=ch=='-'?-1:f;ch=getchar();}
    while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
    return x*f;
}
void write(int x)
{
    if(x<0){x=-x;putchar('-');}
    if(x>9)write(x/10);
    putchar(x%10+48);
}
int n,c[500005];dl ans;
char s[500005];
int check(int x)
{
    if(x=='I'||x=='E'||x=='A'||x=='O'||x=='U'||x=='Y')return 1;
    return 0;
}
signed main()
{
    scanf("%s",s+1);n=strlen(s+1);
    for(int i=1;i<=n;++i)
    {
        if(!check(s[i]))continue;
        int l=i,r=n-i+1;
        c[1]++;c[l+1]--;
        c[r+1]--;c[l+r]++;
    }
    for(int i=1;i<=n;++i)c[i]+=c[i-1];
    for(int i=1;i<=n;++i)c[i]+=c[i-1];
    for(int i=1;i<=n;++i)ans+=(dl)c[i]/i;
    printf("%.8lf",ans);
    return 0;
}