李超线段树
李超线段树
这是个维护平面上线段或直线的数据结构，常用来解决计算几何相关的题目，如：斜率优化DP。
模板：洛谷P4097 [HEOI2013]Segment
题目描述
要求在平面直角坐标系下维护两个操作：
- 在平面上加入一条线段。记第 \(i\) 条被插入的线段的标号为 \(i\) 。
- 给定一个数 \(k\) ，询问与直线 \(x = k\) 相交的线段中，交点纵坐标最大的线段的编号。
输入格式
本题输入强制在线。
输入的第一行是一个整数 \(n\) ，代表操作的个数。
接下来 \(n\) 行，每行若干个用空格隔开的整数，第 \((i + 1)\) 行的第一个整数为 \(op\) ，代 表第 \(i\) 次操作的类型。
若 \(op = 0\) ，则后跟一个整数 \(k\) ，代表本次操作为查询所所有与直线 \(x = (k + lastans - 1) \bmod 39989 + 1\) 相交的线段中，交点纵坐标最大的线段编号。
若 \(op = 1\) ，则后跟四个整数 \(x_0, y_0, x_1, y_1\) ，记 \(x_i' = (x_i + lastans - 1) \bmod 39989 + 1\) ，\(y_i' = (y_i + lastans - 1) \bmod 10^9 + 1\) 。本次操作为插入一条两端点分别为 \((x_0', y_0'),(x_1',y_1')\) 的线段。
其中 \(lastans\) 为上次询问的答案，初始时，\(lastans = 0\) 。
输出格式
对于每次查询，输出一行一个整数，代表交点纵坐标最大的线段的编号。若不存在任何一条线段与查询直线有交，则输出 \(0\) ；若有多条线段与查询直线的交点纵坐标都是最大的，则输出编号最小的线段，同时 \(lastans\) 也应更新为编号最小的一条线段。
解法
题目大意是，在一个二维平面上，依次加入若干条线段，询问对于某个 \(x\) 的最大值，强制在线
李超树像普通线段树一样同样支持两种操作：插入和查询
插入
在李超树上每个节点 \([l,r]\) ，存了一个优势线段，这条线段在 \(mid\) 的值是最大的
考虑在区间 \([L,R]\) 插入一条线段 \(l_0\) ，每到一个线段树上区间被 \([L,R]\) 完全覆盖的节点，与节点上存的优势线段 \(l_1\) 比较
- 如果 \(l_0\) 在 \(x=mid\) 上的值比 \(l_1\) 大，显然这个节点的优势线段变成了 \(l_0\) ，\(swap\;l_0\) 和 \(l_1\)
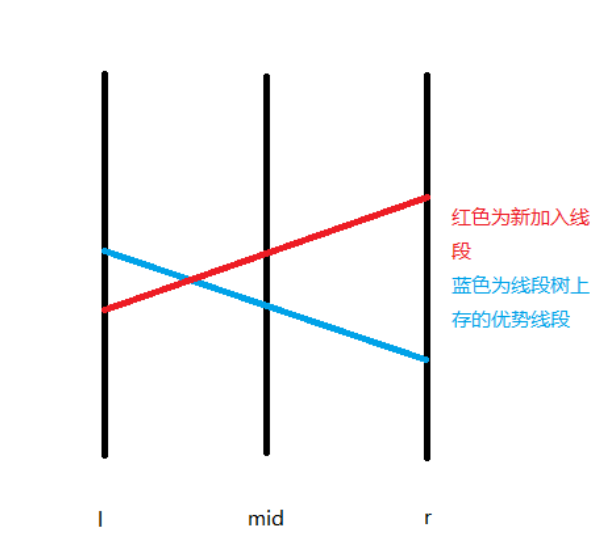
- 如果 \(l_0\) 在 \(x=l\) 上的值比 \(l_1\) 大，要么 \(l_0\) 在 \([l,mid]\) 这段区间覆盖了 \(l_1\) ，或者 \(l_0\) 与 \(l_1\) 在 \([l,mid]\) 中有交点，递归到左区间
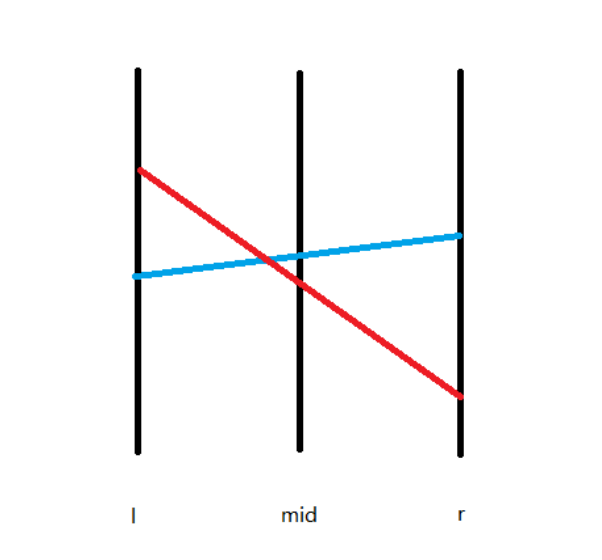
- 如果 \(l_0\) 在 \(x=r\) 上的值比 \(l_1\) 大，要么 \(l_0\) 在 \([mid + 1,r]\) 这段区间覆盖了 \(l_1\) ，或者 \(l_0\) 与 \(l_1\) 在 \([mid+1,r]\) 中有交点，递归到右区间
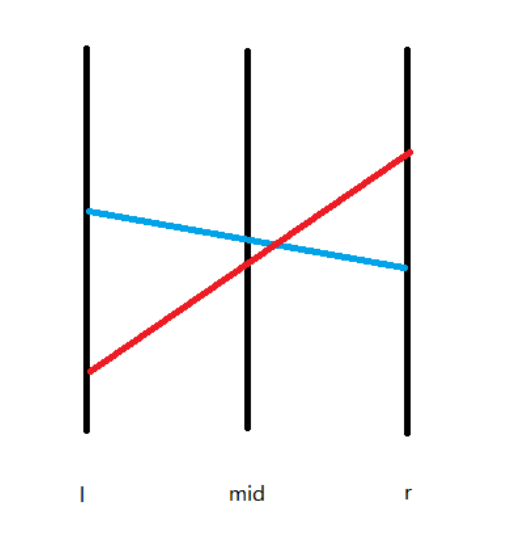
\(swap\;l_0\) 和 \(l_1\) 是因为，如果 \(l_0\) 成为了这个区间的优势线段，那么 \(l_1\) 也有可能与 \(l_0\) 从而递归到儿子区间
我们需要将原线段分割到 \(logn\) 个区间中，对于每个区间，我们又需要花费 \(O(logn)\) 的时间更新该区间以及其子区间的优势线段，从而插入过程的时间复杂度为 \(O(log^2n)\) 。
查询
查询对于某个 \(x=k\) 的极值，在李超树上向下递归，用所有包含它的线段树区间的优势线段求出若干个值，一块取个 \(\max\) 就是答案，时间复杂度 \(O(logn)\) 。
考虑为什么正确，首先我们插入一条线段时，当且仅当当前的优势线段完全覆盖了这个条线段，才会把这个线段舍去，所以不会影响答案的正确性
然后考虑为什么把路径上的所有值都求一遍，因为这个节点存的线段可能与儿子节点的线段有交点，到底取哪个线段作为最大值并不确定，所以把路径上的都求一遍取个最大值。
李超树代码
#include<bits/stdc++.h>
#define dl double
#define ls (pos<<1)
#define rs (pos<<1|1)
using namespace std;
inline int read()
{
int x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){f=ch=='-'?-1:f;ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
return x*f;
}
const int mn=1e5;
const int mod=39989;
const dl eps=1e-8;
int n,tr[mn<<4],cnt;
struct LC_line{dl k,b;}a[mn];
dl calc(LC_line Line,int x){return Line.k*x+Line.b;}
void solve(int X0,int Y0,int X1,int Y1)
{
if(X0==X1)a[++cnt].k=0.0,a[cnt].b=(dl)max(Y0,Y1);
else a[++cnt].k=(dl)(Y0-Y1)/(X0-X1),a[cnt].b=(dl)Y0-a[cnt].k*X0;
}
void change(int pos,int l,int r,int L,int R,int x)
{
int mid=(l+r)>>1;
if(L<=l&&r<=R)
{
if(calc(a[x],mid)-calc(a[tr[pos]],mid)>eps)swap(tr[pos],x);
if(calc(a[x],l)-calc(a[tr[pos]],l)>eps)change(ls,l,mid,L,R,x);
if(calc(a[x],r)-calc(a[tr[pos]],r)>eps)change(rs,mid+1,r,L,R,x);
return;
}
if(L<=mid)change(ls,l,mid,L,R,x);
if(R>mid) change(rs,mid+1,r,L,R,x);
}
int query(int pos,int l,int r,int x)
{
if(l==r){return tr[pos];}int mid=(l+r)>>1,tmp=0;
if(x<=mid)tmp=query(ls,l,mid,x);
else tmp=query(rs,mid+1,r,x);
return calc(a[tmp],x)>calc(a[tr[pos]],x)?tmp:tr[pos];
}
int main()
{
n=read();int lastans=0;
while(n-->0)
{
int opt=read();
if(!opt)
{
int x=(read()+lastans-1)%mod+1;
printf("%d\n",lastans=query(1,1,mod,x));
}
else
{
int X0=read(),Y0=read(),X1=read(),Y1=read();
X0=(X0+lastans-1)%mod+1;Y0=(Y0+lastans-1)%(int)(1e9)+1;
X1=(X1+lastans-1)%mod+1;Y1=(Y1+lastans-1)%(int)(1e9)+1;
if(X0>X1)swap(X0,X1),swap(Y0,Y1);
solve(X0,Y0,X1,Y1);change(1,1,mod,X0,X1,cnt);
}
}
return 0;
}
后记
李超线段树不怎么考，涉及计算几何方面的知识，一般在维护斜率的题目中较为常用，实用性有限，用处不是很多。
