矩阵树定理
矩阵树定理的应用离不开行列式与高斯消元法。
行列式
定义:
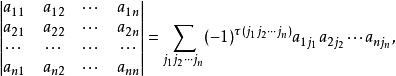
一些基本性质,高斯消元的基础
- 交换行列式的两行,行列式取相反数
这个就是高斯消元的重点之一了,每次转换相邻两行,值相应地取相反数。
因为转换后顺逆序会相反。既然相反就求相反数。
- 行列式的某一行的所有元素都乘以同一数k,等于用数k乘此行列式
注意是只乘一行而不是全部。因为这一行的数字在每个项都出现提出来就行了。
- 行列式如果有两行元素成比例,则此行列式等于零
很神奇,要用到上面两个性质:
记\(f[i]=f[j]\times k\),那么行列式的值就等于转换后的行列式\(\times k\),交换f[i]和f[j]该行列式等于相反数,但显然值不变,所以它=0 , \(0\times k=0\) ,得证。
-
把行列式的某一行的各元素乘以同一数然后加到另一行对应的元素上去,行列式不变
证明:
欲证\(\begin{vmatrix}a&b&c\\.&.&.\\d&e&f\end{vmatrix}=\begin{vmatrix}a&b&c\\.&.&.\\d+ka&e+kb&f+kc\end{vmatrix}\)
首先构造一个\(\begin{vmatrix}a&b&c\\.&.&.\\a&b&c\end{vmatrix}\),根据(3)得其值为0.
又根据(3)得\(\begin{vmatrix}a&b&c\\.&.&.\\ka&kb&kc\end{vmatrix}\)也为0。
然后根据(3)得\(\begin{vmatrix}a&b&c\\.&.&.\\d+ka&e+kb&f+kc\end{vmatrix}=\begin{vmatrix}a&b&c\\.&.&.\\d&e&f\end{vmatrix}+\begin{vmatrix}a&b&c\\.&.&.\\ka&kb&kc\end{vmatrix}=\begin{vmatrix}a&b&c\\.&.&.\\d&e&f\end{vmatrix}\)
高斯消元的重点。
- 若行列式的某一行每一个元素都可以由两个数相加得到,则这个行列式是对应两个行列式的和
这个很简单,用乘法分配律就可以证。
\(\begin{vmatrix}a+a'&b+b'\\c&d\end{vmatrix}=\begin{vmatrix}a&b\\c&d\end{vmatrix}+\begin{vmatrix}a'&b'\\c&d\end{vmatrix}\)
高斯消元主要用于第一个和第四个性质。它把行列式下三角全变为0。依据性质,我们知道此时行列式的值就是对角线的积。
高斯消元求行列式(取模意义下)的代码:
#include<bits/stdc++.h>
#define int long long
using namespace std;
inline int read()
{
int x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){f=ch=='-'?-1:f;ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
return x*f;
}
inline void write(int x)
{
if(x<0){x=-x;putchar('-');}
if(x>9)write(x/10);
putchar(x%10+48);
}
const int mod=1e9+7;
int n,ans=1;
int a[1005][1005];
int ksm(int x,int y,int mod)
{
int res=1;
while(y)
{
if(y&1)res=res*x%mod;
x=x*x%mod;y>>=1;
}return res;
}
signed main()
{
n=read();
for(int i=1;i<=n;++i)
for(int j=1;j<=n;++j)
a[i][j]=read();
for(int i=1;i<=n;++i)
{
int row=i;
while(!a[row][i]&&row<=n)++row;
if(row>n)break;
if(row!=i)swap(a[i],a[row]),ans=-ans;
int inv=ksm(a[i][i],mod-2,mod);
for(int j=i+1;j<=n;++j)
{
int tmp=a[j][i]*inv%mod;
for(int k=i;k<=n;++k)
a[j][k]=(a[j][k]-a[i][k]*tmp%mod+mod)%mod;
}
}
for(int i=1;i<=n;++i)ans=(ans*a[i][i]%mod+mod)%mod;
write(ans);putchar('\n');
return 0;
}
/*
3
1 2 3
4 5 6
7 8 0
ans:27
*/
Matrix-Tree 定理
前置知识:我们用到的矩阵,也就是基尔霍夫矩阵的任意一个代数余子式是所有生成树的边权积的和。
当所有边边权为1时求的就是生成树的个数了。
我们以下设 \((x,y,z)\) 为 \(x\) 到 \(y\) 有一条边权为 \(z\) 的无向/有向边。
1.无向图
假设现在给定一个图 \(G\) 。
度数矩阵 \(D\) :若存在边 \((x,y,z)\) ,则 \(D[x][x]+=z~;D[y][y]+=z~;\)
邻接矩阵 \(C\) :若存在边 \((x,y,z)\) ,则 \(C[x][y]+=z~;C[y][x]+=z~;\)
图G的基尔霍夫矩阵 \(A = D − C\) 。
删去任意一行和任意一列,求剩下的矩阵行列式即可。
2.有向图
假设现在给定一个图 \(G\) 。
度数矩阵D:若存在边 \((x,y,z)\) ,则 外向树中 \(D[y][y]+=z~;\) 内向树中 \(D[x][x]+=z~;\)
邻接矩阵C:若存在边 \((x,y,z)\) ,则 内向树和外向树中均为 \(C[x][y]+=z~;\)
图G的基尔霍夫矩阵 \(A = D − C\) 。
删去指定的根所在的行和列,求剩下的矩阵行列式即可。
求矩阵行列式用高斯消元法即可,时间复杂度 \(O(n^3)\) 。
代码:
#include<bits/stdc++.h>
#define int long long
using namespace std;
inline int read()
{
int x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){f=ch=='-'?-1:f;ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
return x*f;
}
inline void write(int x)
{
if(x<0){x=-x;putchar('-');}
if(x>9)write(x/10);
putchar(x%10+48);
}
const int mod=1e9+7;
int n,m,t,ans=1,a[500][500];
int ksm(int x,int y,int mod)
{
int res=1;
while(y)
{
if(y&1)res=res*x%mod;
x=x*x%mod;y>>=1;
}return res;
}
void work()
{
for(int i=2;i<=n;++i)
{
int row=i;
while(!a[row][i]&&row<=n)++row;
if(row>n)return;
if(row!=i)swap(a[row],a[i]),ans=-1;
int inv=ksm(a[i][i],mod-2,mod);
for(int j=i+1;j<=n;++j)
{
int tmp=a[j][i]*inv%mod;
for(int k=i;k<=n;++k)
a[j][k]=(a[j][k]-a[i][k]*tmp%mod+mod)%mod;
}
}
}
signed main()
{
n=read(),m=read(),t=read();
for(int i=1;i<=m;++i)
{
int u=read(),v=read(),w=read();
if(!t)
{
(a[u][u]+=w)%=mod,(a[v][v]+=w)%=mod;
(a[u][v]-=w)%=mod,(a[v][u]-=w)%=mod;
}
else (a[v][v]+=w)%=mod,(a[u][v]-=w)%=mod;
}work();
for(int i=2;i<=n;++i)ans=(ans*a[i][i])%mod;
write(ans);putchar('\n');
return 0;
}
后记
这玩意用处不大,考的可能也很小,但毕竟是图论的一个重要知识,还是有必要学的。(关于生成树)


 浙公网安备 33010602011771号
浙公网安备 33010602011771号