对数几率回归（逻辑回归）原理与Python实现

目录

• 一、对数几率和对数几率回归
• 二、Sigmoid函数
• 三、极大似然法
• 四、梯度下降法
• 四、Python实现

一、对数几率和对数几率回归

  在对数几率回归中，我们将样本的模型输出\(y^*\)定义为样本为正例的概率，将\(\frac{y^*}{1-y^*}\)定义为几率（odds），几率表示的是样本作为正例的相对可能性。将几率取对便可以得到对数几率（log odds，logit）。

\[logit=\log\frac{y^*}{1-y^*} \]

  而对数几率回归（Logistic Regression）则试图从样本集中学得模型\(w^Tx\)并使其逼近该样本的对数几率，从而可以得到：

\[condition1:w^Tx=\log\frac{y^*}{1-y^*} \]

二、Sigmoid函数

  通过求解\(conditoin1\)可以得到：

\[y^*=\frac{e^{w^Tx}}{1+e^{w^Tx}}=\frac{1}{1+e^{-w^Tx}} \]

  由此我们可以知道样本\(x_i\)为正例的概率可以通过函数\(h(w^Tx_i)=\frac{1}{1+e^{-w^Tx_i}}\)来表示。而其中的函数\(h(z)\)便被称为Sigmoid函数，其图像如下：

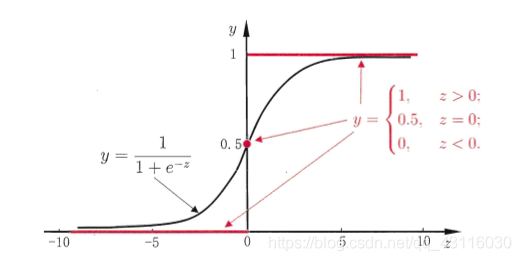
  求其导数：

\[h'(z)=\frac{-e^{-z}}{(1+e^{-z})^2}=\frac{1}{1+e^{-z}}(1-\frac{1}{1+e^{-z}})=h(z)(1-h(z)) \]

这是一个很好的性质，有利于简化后面优化模型时的计算。

三、极大似然法

  通过前面的推导，可以得到：

\[P(y=1|x)=y^*=h(w^Tx)\,\,\,\,\,\,\,\,P(y=0|x)=1-y^*=1-h(w^Tx) \]

合并两个式子，则有：

\[P(y|x)=h(w^Tx)^y(1-h(w^Tx))^{1-y} \]

  求出了样本标记的分布律，便可以通过极大似然法来估计分布律中的参数\(w\)。先写出极大似然函数：

\[L(y_i|x_i,w)=\prod^{m}_{i=1}h(w^Tx_i)^{y_i}(1-h(w^Tx_i))^{1-{y_i}} \]

  对极大似然函数取对可以得到对数似然函数：

\[l(y_i|x_i,w)=log(L)=\sum^{m}_{i=1}{(y_i\log h(w^Tx_i)+(1-y_i)log(1-h(w^Tx_i)))} \]

  在前面乘上负数因子便可以得到对数几率回归的代价函数：

\[J(w)=-\frac{1}{m}\sum^{m}_{i=1}{(y_i\log h(w^Tx_i)+(1-y_i)log(1-h(w^Tx_i)))} \]

通过最小化上述代价函数便可以估计出参数\(w\)的值。

四、梯度下降法

  通过上述步骤，优化对数几率回归模型的关键变成了求解：

\[w=\arg\min J(w)=\arg\min -\frac{1}{m}\sum^{m}_{i=1}{(y_i\log h(w^Tx_i)+(1-y_i)log(1-h(w^Tx_i)))} \]

  在《线性回归：梯度下降法优化》中，我已经详细介绍了梯度下降法的数学原理，这里直接使用梯度下降法来对对数几率回归模型进行优化。
  对\(J(w)\)进行求导：

\[\frac{\partial J}{\partial w}=-\frac{1}{m}\sum^{m}_{i=1}(y_i(1-h(w^Tx_i))x_i+(y_i-1)h(w^Tx_i)x_i)=-\frac{1}{m}\sum^{m}_{i=1}{(y_i-h(w^Tx_i))x_i} \]

  将\(\frac{\partial J}{\partial w}\)带入参数\(w\)的更新公式\(w^*=w-\eta\frac{\partial J}{\partial w}\)，最终得到\(w\)的更新公式如下：

\[w^*=w+\frac{\eta}{m}\sum^{m}_{i=1}{(y_i-h(w^Tx_i))x_i} \]

四、Python实现

  梯度下降优化算法：

    def fit(self, X, y):
        self.W = np.zeros(X.shape[1] + 1)
        for i in range(self.max_iter):
            delta = self._activation(self._linear_func(X)) - y
            self.W[0] -= self.eta * delta.sum()
            self.W[1:] -= self.eta * (delta @ X)
        return self

  导入鸢尾花数据集进行测试：

if __name__ == "__main__":
    from sklearn import datasets
    from sklearn.model_selection import train_test_split
    from sklearn.metrics import classification_report

    irirs = datasets.load_iris()
    X = irirs["data"][:100]
    y = irirs["target"][:100]
    X_train, X_test, y_train, y_test = train_test_split(X, y, train_size=0.7, test_size=0.3)
    classifier = LRClassifier().fit(X_train, y_train)
    y_pred = classifier.predict(X_test)
    print(classification_report(y_test, y_pred))

  分类报告如下：