树链剖分

 

 

•参考资料

　　[1]:博客

　　[2]:论文（提取码：r87c）

•抛出问题

　　给定一棵有 $n$ 个节点、带边权的树；

　　现在要对树进行 $m$ 个操作，操作有2类：

    • 将节点 $a$ 到节点 $b$ 路径上所有边权的值都改为 $c$

    • 询问节点 $a$ 到节点 $b$ 路径上的最大边权值

•问题的解

　　树链剖分是指一种对树进行划分的算法，它先通过轻重边剖分（Heavy-Light Decomposition）将树分为多条链；

　　保证每个点属于且只属于其中一条链，然后再通过数据结构（树状数组、SBT、SPLAY、线段树等）来维护每一条链。

　　使用这种方法后，一般可以将修改和查询的复杂度降为 $O(logn)$。

•树链剖分的方法

  • 将树中的边分为：重边和轻边

  • 定义 $size(x)$ 为以 $x$ 为根的子树的节点个数
  • 令 $v$ 为 $u$ 的儿子节点中 $size$ 值最大的节点，那么 $v$ 称为 $u$ 的重儿子，边 $(u,v)$ 被称为重边
  • 树中重边之外的边被称为轻边
  • 全部由重边构成的路径称为重链

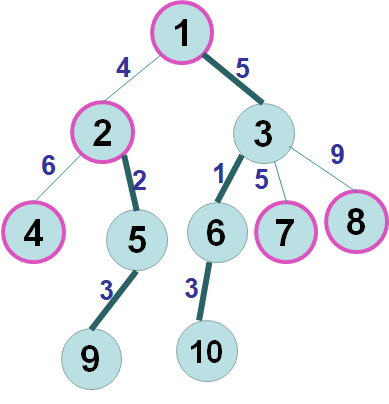
　　例如，图中有5条重链：

　　　　1→3→6→10
　　　　2→5→9
　　　　4
　　　　7
　　　　8

　　相关变量解释：

    • $siz[i]$ : 以结点 $i$ 为根的子树中结点的个数
    • $son[i]$ : 结点 $i$ 的重儿子
    • $dep[i]$ : 结点 $i$ 的深度，根的深度为 $0$
    • $top[i]$ : 结点 $i$所在重链的链首结点
    • $fa[i]$ : 结点$i$的父结点
    • $tid[i]$ : 在 $DFS$ 找重链的过程中为结点 $i$ 重新编的号码，每条重链上的结点编号是连续的
    • $rid[i]$ : 与 $tid$ 的作用正好相反，编号 $i$ 对应的节点编号

•树链剖分的过程

  •  两次 $DFS$
  • 第一次 $DFS$ 找重边，顺便求出所有的 $siz[i],dep[i],fa[i],son[i]$
  • 第二次DFS将重边连成重链，顺便求出所有的 $top[i],tid[i],rid[i]$
 1 void DFS1(int u,int f,int depth)///第一遍DFS求出fa,dep,siz,son
 2 {
 3     fa[u]=f;
 4     siz[u]=1;
 5     dep[u]=depth;
 6     for(int i=head[u];~i;i=G[i].next)
 7     {
 8         int v=G[i].to;
 9         
10         if(v == f)///此处是v == f才continue，在这儿出过错
11             continue;
12             
13         DFS1(v,u,depth+1);
14         
15         siz[u] += siz[v];
16         if(son[u] == -1 || siz[v] > siz[son[u]])///更新u的重儿子
17             son[u]=v;
18     }
19 }
DFS1
 1 void DFS2(int u,int anc,int &k)///第二遍DFS求出 tid,rid,top
 2 {
 3     top[u]=anc;
 4     tid[u]=++k;
 5     rid[k]=u;
 6     if(son[u] == -1)
 7         return ;
 8     DFS2(son[u],anc,k);
 9 
10     for(int i=head[u];~i;i=G[i].next)
11     {
12         int v=G[i].to;
13         if(v != son[u] && v != fa[u])
14             DFS2(v,v,k);
15     }
16 }
DFS2

　　入门题：http://www.cnblogs.com/kuangbin/p/3253741.html

 

posted @ 2018-09-27 09:38  HHHyacinth  阅读(344)  评论(0)  编辑  收藏  举报