BZOJ 4034"树上操作"（DFS序+线段树）

 

传送门

 

•题意

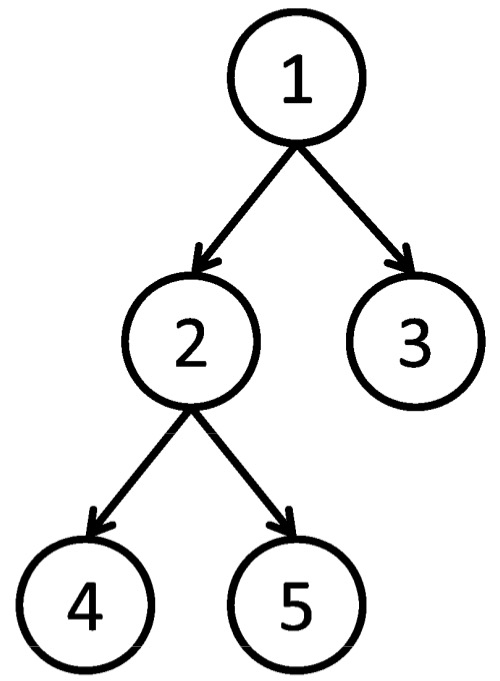
　　有一棵点数为 N 的树，以点 1 为根，且树点有边权。

　　然后有 M 个操作，分为三种：

　　　　操作 1 ：把某个节点 x 的点权增加 a 。
　　　　操作 2 ：把某个节点 x 为根的子树中所有点的点权都增加 a 。
　　　　操作 3 ：询问某个节点 x 到根的路径中所有点的点权和。
　　输出操作 3 对应的答案；

•题解

　　如果可以将树形结构转化成链式结构，那么，操作 1，2 就可以用线段树来维护；

　　$1,2,4,4,5,5,2,3,3,1$

　　定义 $s,e$ 分别记录每个节点在序列中第一次出现的位置和最后一次出现的位置；

　　那么，第一次出现的位置权值为正，最后一次出现的位置权值为负；

　　这样的话，就可以通过线段树来维护；

　　操作 1 就对应线段树中的单点更新操作；

　　操作 2 就对应线段树中的区间更新操作；

　　操作 3 就是区间查询操作；

•Code

  1 #include<bits/stdc++.h>
  2 using namespace std;
  3 #define ll long long
  4 #define ls(x) (x<<1)
  5 #define rs(x) (x<<1|1)
  6 #define mem(a,b) memset(a,b,sizeof(a))
  7 const int maxn=1e5+50;
  8 
  9 int n,m;
 10 int a[maxn];
 11 int num;
 12 int head[maxn];
 13 struct Edge
 14 {
 15     int to;
 16     int next;
 17 }G[maxn<<1];
 18 void addEdge(int u,int v)
 19 {
 20     G[num]={v,head[u]};
 21     head[u]=num++;
 22 }
 23 struct Seg
 24 {
 25     int l,r;
 26     ll lazy;
 27     ll sum;
 28     int x;///沿叶子方向的节点个数
 29     int y;///沿根方向的节点个数
 30     int mid(){return l+((r-l)>>1);}
 31     void Set(ll val)
 32     {
 33         ///如果[l,r]区间的每个节点都增加val
 34         ///那么，[l,r]区间中沿叶子方向的x个节点增加+val
 35         ///[l,r]区间中沿根方向的y个节点增加-val
 36         lazy += val;
 37         sum += 1ll*(x-y)*val;
 38     }
 39 }seg[maxn<<3];
 40 int cnt;
 41 int s[maxn];
 42 int e[maxn];
 43 int vs[maxn<<1];
 44 bool g[maxn<<1];
 45 
 46 void DFS(int u,int f)
 47 {
 48     vs[++cnt]=u;
 49     s[u]=cnt;
 50     g[cnt]=1;
 51     for(int i=head[u];~i;i=G[i].next)
 52     {
 53         int v=G[i].to;
 54         if(v != f)
 55             DFS(v,u);
 56     }
 57     vs[++cnt]=u;
 58     e[u]=cnt;
 59     g[cnt]=0;
 60 }
 61 void pushUp(int pos)
 62 {
 63     seg[pos].x=seg[ls(pos)].x+seg[rs(pos)].x;
 64     seg[pos].y=seg[ls(pos)].y+seg[rs(pos)].y;
 65     seg[pos].sum=seg[ls(pos)].sum+seg[rs(pos)].sum;
 66 }
 67 void pushDown(int pos)
 68 {
 69     ll &lazy=seg[pos].lazy;
 70     if(!lazy)
 71         return ;
 72 
 73     seg[ls(pos)].Set(lazy);
 74     seg[rs(pos)].Set(lazy);
 75 
 76     lazy=0;
 77 }
 78 void build(int l,int r,int pos)
 79 {
 80     seg[pos]={l,r,0,0,0,0};
 81 
 82     if(l == r)
 83     {
 84         if(g[l])
 85         {
 86             seg[pos].x++;
 87             seg[pos].sum=a[vs[l]];
 88         }
 89         else
 90         {
 91             seg[pos].y++;
 92             seg[pos].sum=-a[vs[l]];
 93         }
 94 
 95         return ;
 96     }
 97 
 98     int mid=seg[pos].mid();
 99     build(l,mid,ls(pos));
100     build(mid+1,r,rs(pos));
101 
102     pushUp(pos);
103 }
104 void update(int pos,int l,int r,int x)
105 {
106     if(seg[pos].l == l && seg[pos].r == r)
107     {
108         seg[pos].Set(x);
109         return ;
110     }
111     pushDown(pos);
112 
113     int mid=seg[pos].mid();
114     if(r <= mid)
115         update(ls(pos),l,r,x);
116     else if(l > mid)
117         update(rs(pos),l,r,x);
118     else
119     {
120         update(ls(pos),l,mid,x);
121         update(rs(pos),mid+1,r,x);
122     }
123     pushUp(pos);
124 }
125 ll query(int pos,int l,int r)
126 {
127     if(seg[pos].l == l && seg[pos].r == r)
128         return seg[pos].sum;
129     pushDown(pos);
130 
131     int mid=seg[pos].mid();
132     if(r <= mid)
133         return query(ls(pos),l,r);
134     else if(l > mid)
135         return query(rs(pos),l,r);
136     else
137         return query(ls(pos),l,mid)+query(rs(pos),mid+1,r);
138 }
139 void Solve()
140 {
141     cnt=0;
142     DFS(1,1);
143     build(1,cnt,1);
144 
145     while(m--)
146     {
147         int op;
148         scanf("%d",&op);
149         if(op == 1)
150         {
151             int u,x;
152             scanf("%d%d",&u,&x);
153             update(1,s[u],s[u],x);
154             update(1,e[u],e[u],x);
155         }
156         else if(op == 2)
157         {
158             int u,x;
159             scanf("%d%d",&u,&x);
160             update(1,s[u],e[u],x);
161         }
162         else
163         {
164             int u;
165             scanf("%d",&u);
166             printf("%lld\n",query(1,s[1],s[u]));
167         }
168     }
169 }
170 void Init()
171 {
172     num=0;
173     mem(head,-1);
174 }
175 int main()
176 {
177 //    freopen("C:\\Users\\hyacinthLJP\\Desktop\\C++WorkSpace\\in&&out\\contest","r",stdin);
178     scanf("%d%d",&n,&m);
179     for(int i=1;i <= n;++i)
180         scanf("%d",a+i);
181 
182     Init();
183     for(int i=1;i < n;++i)
184     {
185         int u,v;
186         scanf("%d%d",&u,&v);
187         addEdge(u,v);
188         addEdge(v,u);
189     }
190     Solve();
191 
192     return 0;
193 }
View Code

•变形

　　此题操作 3 还可改成求解 $u,v$ 路径间的节点权值和；

　　只需在原来的基础上增加个求解 $LCA$ 的代码即可；

posted @ 2019-11-02 16:58  HHHyacinth  阅读(173)  评论(0)  编辑  收藏  举报