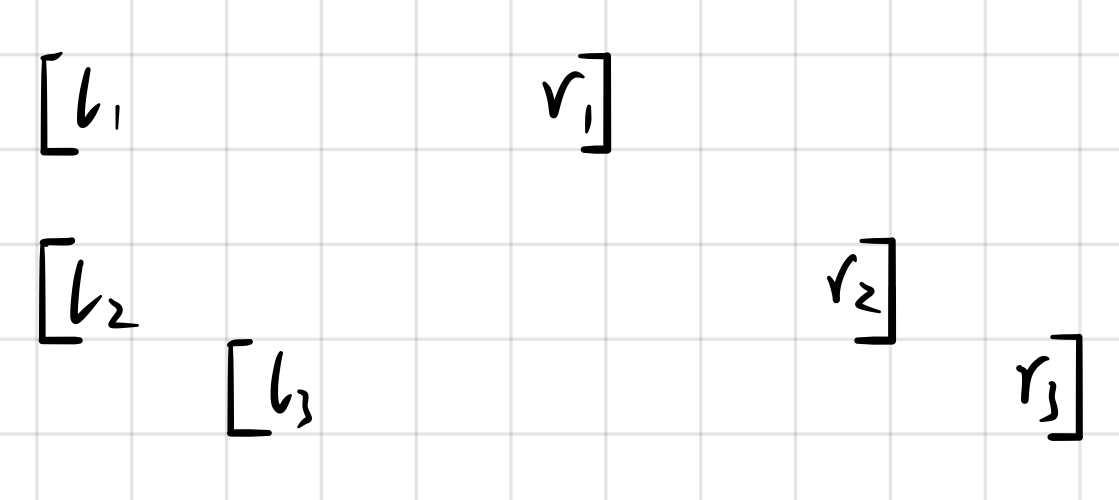The Preliminary Contest for ICPC Asia Shanghai 2019

 

传送门

 

B.Light bulbs（思维）

•题意

　　有 n 个灯泡，初始全部为关闭状态；

　　有 m 个操作，每次操作给出 [l,r]，让你将区间 [l,r] 的灯泡反转。

　　问最终有多少灯泡是亮着的；

　　其中有 T 组数据，T ≤ 1000 , n ≤ 10⁶ , m ≤ 1000；

•题解

　　刚开始想着差分，这样的话，O(n) 就可以解出这道题；

　　但是，题干中并没有说 $\sum_{1}^{T} n \le 10^8$，所以，很有可能有 1000 组数据，每组数据的 n = 10⁶ 的情况；

　　这样的话，O(n) 的做法就凉凉；

　　T 了几发后，换思路；

　　想到了扫描线，对于输入的 m 个 [l,r]，离线处理，存到如下数据结构中：

struct Data
{
    int x;///l or r
    int f;///f=1:x为l , f=-1:x为r
    bool operator < (const Data &obj) const
    {
        return x < obj.x;
    }
}a[4*maxn];

　　$a[++k]=\{l,1\}\ ,\ a[++k]=\{r,-1\}$

　　并额外存储如下信息：

　　$a[++k]=\{l-1,0\}\ ,\ a[++k]=\{r+1,0\}$

　　即用 f = 0 代表存入的是额外加入的信息；

　　首先按照 x 升序排列；

　　然后，求出所有不同的 x 对应的反转次数，最后统计一下答案即可；

•Code

　　2019ICPC上海网络赛B.cpp

 

•简单做法

　　类比差分的做法，定义数组 a，其中 a[i] 存储反转区间的端点；

　　对于某一反转区间 [l,r]，将 l 和 r+1 存入 a 数组中，并将 a 升序排列；

int k=0;
for(int i=1;i <= m;++i)
{
    int l,r;
    scanf("%d%d",&l,&r);

    a[++k]=l;
    a[++k]=r+1;
}
sort(a+1,a+k+1);

　　存储完这些信息后，如何统计答案呢？

　　模拟一下，你会发现，这 k 个数，两两组成一队，$a_1 \ to\  a_2 \ ,\ a_3 \ to\ a_4 \ ,\cdots \ ,\ a_{k-1} \ to\ a_{k}$；

　　并且这 $\frac{k}{2}$ 对，除了右区间 $a_2\ ,\ a_4\ ,\ \cdots \ ,\ a_k$ 对应的灯泡被反转了偶数次外；

　　$a_1 \ to\  a_2 -1 \ ,\ a_3 \ to\ a_4 -1 \ ,\cdots \ ,\ a_{k-1} \ to\ a_{k}-1$ 对应的灯泡被反转了奇数次；

　　如图：

　　

　　排序后，a 中存储的信息如下：

　　$\begin{aligned}&a_1 = l_1\ ,\ a_2 = l_2 \\ &a_3=l_3 \ ,\ a_4=r_1 +1 \\ &a_5=r_2+1 \ ,\ a_6=r_3+1 \end{aligned}$

　　$ans=a_2-a_1+a_4-a_3+a_6-a_5$;

　　利用差分的思想，将 l,r+1 存入 a 中，顺利解决了此题；

•Code

　　2019ICPC上海网络赛B(2).cpp

 

J.Stone game（背包？？？）

•题意

　　有 n 堆（$n \le 300$）石子，第 i 堆有 a_i 个（$a_i \le 500$）石子；

　　让你从这 n 堆石子中任意抽取出 x 堆（第$p_1,p_2,\cdots ,p_x$），使得满足如下条件：

　　　　（1）$define\ sum_1=\sum_{i=1}^{x}a_{p_i}\ ,\ sum_2 = \sum_{i=1}^{n}a_i \ - sum_1$

　　　　（2）$sum_1 \ge sum_2\ \&\& \ sum_1 - a_{p_t} \le sum_2\ ,\ t \in [1,x]$

　　求满足条件的取法对 $10^9 +7$ 取模的结果；

•题解

　　看到这个题的时候，看了一下 n ，才 300，想了想，会不会是区间DP；

　　找了一会转移方程，没找到，然后，觉得，如果这道题是区间DP的话，为什么 $a_i$ 还那么小；

　　算了一下 $max(\sum_{i=1}^{n}a_i )\le 150000$，并且此题还给开了 3s；

　　然后，想了一下，最大的 sum 都可以用数组存下，会不会需要开个这么大的数组存储所有的可能出现的加和；

　　然后，就有了如下想法；

　　首先，按照 a 升序排列；

　　假设将这 n 堆石子划分成了 u,v 两堆，$|u|=sum_1\ ,\ |v|=sum_2$；

　　定义 dp[ i ] 表示 $a_i$ 作为 u 堆中的最小的那一堆石子时的总方案数；

　　定义 b[ i ][ j ] 表示 [i+1,n] 堆石子可以组成 j 个石子的方案数；

　　类似于背包问题，按照 a 降序的方向处理即可；

•Code

　　2019ICPC上海网络赛J.cpp