2019牛客暑期多校训练营（第二场）

传送门

 

参考资料：

　　[1]:官方题解（提取码：ar7y）

　　[2]:标程（提取码：3qb2）

 

A.Eddy Walker（概率+打表找规律）

•题意

　　有一个圆，圆上有 n 个点，编号为 0~n-1；

　　初始，Eddy 处于 0 位置，每次他独立地均匀随机选择是向前（0+1）还是向后（0-1 = n-1）走；

　　现给你 n,m ，让你求 Eddy 在走 n 步后停留在 m 处的概率；

　　最终结果输出前缀积；

•题解

　　在补这道题前，补了补概率论的相关概念；

　　1.频率定义

　　　　若在相同的条件下进行的 n 次试验中，事件 A 发生了 m 次，则称比值 m / n 为事件 A 发生的频率；

　　2.概率的统计定义

　　　　在相同条件下进行大量重复试验，当试验次数充分大时，事件 A 的频率将在某个常数 p 附近摆动，
　　　　这个常数 p 称为事件 A 的概率，记为 P(A)；

　　有了这些概念后，找了几篇博文看，发现，要么是达标找规律，要么就是直接写结论，没有严格的数学证明；

　　哎，本蒟蒻太菜，并不擅长概率论方面的题，暂且补补打表找规律的；

 1 #include<bits/stdc++.h>
 2 using namespace std;
 3 #define mem(a,b) memset(a,b,sizeof(a))
 4 const int maxn=100;
 5 
 6 int n;
 7 bool vis[maxn];
 8 int k[maxn];
 9 
10 int main()
11 {
12     srand((unsigned int)(time(NULL)));
13 
14     scanf("%d",&n);///n最好不要太大，不然，不能再有限的时间内跑出结果
15     for(int i=1;i <= 100000;i++)
16     {
17         mem(vis,false);
18         vis[0]=true;
19 
20         int cur=0;
21         int t=1;
22 
23         while(t < n)
24         {
25             int x=rand()%2 ? 1:-1;///向前或向后走
26             cur=(cur+x+n)%n;
27 
28             if(!vis[cur])
29             {
30                 vis[cur]=true;
31                 t++;
32             }
33         }
34         k[cur]++;
35     }
36     for(int i=1;i < n;i++)
37         printf("%d ",k[i]);
38     printf("\n");
39 
40     return 0;
41 }
打表找规律

　　当输入的 n = 10 时，大概可以看出除 0 外，其他位置的概率为 1 / (n-1)；

　　0 单独处理；

•Code

 1 #include<bits/stdc++.h>
 2 using namespace std;
 3 #define ll long long
 4 const int MOD=1e9+7;
 5 
 6 ll qPow(ll a,ll b)
 7 {
 8     ll ans=1;
 9     a %= MOD;
10 
11     while(b)
12     {
13         if(b&1)
14             ans=ans*a%MOD;
15 
16         a=a*a%MOD;
17         b >>= 1;
18     }
19     return ans;
20 }
21 ll Inv(ll a)///返回 a 的逆元
22 {
23     return qPow(a,MOD-2)%MOD;
24 }
25 int main()
26 {
27     int T;
28     scanf("%d",&T);
29     
30     ll ans=1;
31     while(T--)
32     {
33         int n,m;
34         scanf("%d%d",&n,&m);
35         ll cur;
36         if(m == 0)
37         {
38             if(n != 1)
39                 cur=0;
40             else
41                 cur=1;
42         }
43         else
44             cur=Inv(n-1);///cur = {1/(n-1)}%MOD;
45         
46         ans=ans*cur%MOD;
47         
48         printf("%lld\n",ans);
49     }
50     return 0;
51 }
View Code

•想法

　　打表找规律做出的题终究不是正解，只能解决当前题；

 

 

F.Partition priblem(DFS)

•题意

　　有 2n 个人，任意两个人之间都存在竞争值；

　　定义 v[ i ][ j ] 表示 i 与 j 的竞争值为 v[ i ][ j ]；

　　现让你将这 2n 个人划分成两组，每组有 n 人，组内的成员之间不存在竞争；

　　求最大的竞争值；

　　例如，假设 a 组有成员 1,2 ， b 组有成员 3,4；

　　其竞争值为 v[1][3] + v[1][4] + v[2][3] + v[2][4]；

•题解

　　DFS+剪枝；

•Code

 1 #include<bits/stdc++.h>
 2 using namespace std;
 3 #define ll long long
 4 const int maxn=100;
 5 
 6 int n;
 7 ll sum;
 8 ll v[maxn][maxn];
 9 ///将这2n个人划分成a,b两组，每组有n人
10 int a[maxn];
11 int b[maxn];
12 
13 ///a组中的成员为a[1],a[2],...,a[cntA-1];
14 ///b组中的成员为b[1],b[2],...,b[cntB-1];
15 ///当前a,b两组的竞争值为cur
16 ///在向a组或b组中增加新成员时，cur -= x;
17 ///x指的是加入新成员后的组内竞争
18 void DFS(int cntA,int cntB,ll cur,ll &ans)
19 {
20     if(ans >= cur)
21         return ;
22     if(cntA-1 > n || cntB-1 > n)
23         return ;
24     
25     int k=cntA+cntB-1;
26     if(k == 2*n+1)
27     {
28         ans=max(ans,cur);
29         return ;
30     }
31     
32     ll tmp=cur;
33     a[cntA]=k;///k归到a组
34     for(int i=1;i < cntA;++i)
35         tmp -= v[a[i]][k];///x=∑v[a[i]][k]
36     DFS(cntA+1,cntB,tmp,ans);
37     
38     tmp=cur;
39     b[cntB]=k;///k归到b组
40     for(int i=1;i < cntB;++i)
41         tmp -= v[b[i]][k];///x=∑v[b[i]][k]
42     DFS(cntA,cntB+1,tmp,ans);
43 }
44 ll Solve()
45 {
46     ll ans=0;
47     DFS(1,1,sum,ans);
48     
49     return ans;
50 }
51 int main()
52 {
53     scanf("%d",&n);
54     
55     sum=0;
56     for(int i=1;i <= n*2;++i)
57         for(int j=1;j <= n*2;++j)
58         {
59             scanf("%lld",v[i]+j);
60             if(j < i)
61                 sum += v[i][j];
62         }
63     printf("%lld\n",Solve());
64     
65     return 0;
66 }
View Code

 

 

H.Second Large Rectangle(单调栈)

•题意

       给你一个仅由 01 组成的 n×m 组成的矩阵；

       求仅由 1 组成的矩阵中，第二大的矩阵面积；

•题解

      定义二维数组 h，h[ i ][ j ] 表示从(i,j) 位置开始向上连续的 1 的个数；

      例如：

　　 

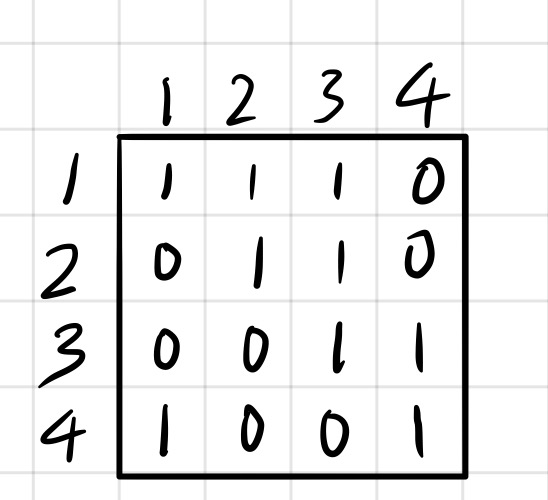
　　h[1][1] = 1 , h[2][1] = 0 , h[3][3] = 3 , h[4][1] = 1;

      对于第 i 行，首先求出 h[ i ][ j ] 后，然后通过单调栈算法求出以 h[ i ][ j ] 为高的最大的矩阵面积； 

　　定义变量 f,s 分别记录第一大和第二大的矩阵的面积及相应的矩阵坐标；

      每到达一个新位置，判断是否需要更新 f,s ；

      最后，输出 s 矩阵所表示的面积；

•Code

  1 #include<bits/stdc++.h>
  2 using namespace std;
  3 const int maxn=5e3+50;
  4  
  5 int n,m;
  6 char a[maxn][maxn];
  7 int h[maxn];
  8 int l[maxn];
  9 int r[maxn];
 10 stack<int >sta;
 11  
 12 struct Data
 13 {
 14     int a,b;
 15     int c,d;
 16     int val;
 17 }f,s;
 18  
 19 void Clear()
 20 {
 21     while(!sta.empty())
 22         sta.pop();
 23 }
 24 void Work()
 25 {
 26     Clear();
 27     for(int i=1;i <= m;++i)
 28     {
 29         while(!sta.empty() && h[sta.top()] >= h[i])
 30             sta.pop();
 31  
 32         l[i]=sta.empty() ? 1:sta.top()+1;
 33         sta.push(i);
 34     }
 35  
 36     Clear();
 37     for(int i=m;i >= 1;--i)
 38     {
 39         while(!sta.empty() && h[sta.top()] >= h[i])
 40             sta.pop();
 41  
 42         r[i]=sta.empty() ? m:sta.top()-1;
 43         sta.push(i);
 44     }
 45 }
 46 void updata(Data &tmp,int a,int b,int c,int d)
 47 {
 48     tmp.a=a;
 49     tmp.b=b;
 50     tmp.c=c;
 51     tmp.d=d;
 52  
 53     tmp.val=(c-a+1)*(d-b+1);
 54 }
 55 int Solve()
 56 {
 57     for(int i=0;i <= m;++i)
 58         h[i]=0;
 59  
 60     f=Data{0,0,0,0,0};
 61     s=Data{0,0,0,0,0};
 62  
 63     for(int i=1;i <= n;++i)
 64     {
 65         for(int j=1;j <= m;++j)
 66         {
 67             if(a[i][j] == '1')
 68                 h[j]++;
 69             else
 70                 h[j]=0;
 71         }
 72  
 73         Work();
 74  
 75         for(int j=1;j <= m;++j)
 76         {
 77             int cur=h[j]*(r[j]-l[j]+1);
 78  
 79             //(a,b) : cur 矩形左上角坐标
 80             //(c,d) : cur 矩形右下角坐标
 81             int a=i-h[j]+1;
 82             int b=l[j];
 83             int c=i;
 84             int d=r[j];
 85  
 86             if(cur >= f.val)
 87             {
 88                 if(!(a == f.a && b == f.b && c == f.c && d == f.d))
 89                     s=f;//如果当前面积 cur 所表示的矩形不等于 f 所表示的矩形
 90  
 91                 updata(f,a,b,c,d);
 92             }
 93             else if(cur >= s.val)
 94                 updata(s,a,b,c,d);
 95  
 96             //cur矩形在减少一行或一列后肯定不等于 f 所表示的矩形
 97             int cutX=(c-a)*(d-b+1);//减少一行后，判断是否更新 s
 98             int cutY=(c-a+1)*(d-b);//减少一列后，判断是否更新 s
 99  
100             //判断是否更新 s
101             if(cutX > s.val)
102                 updata(s,a+1,b,c,d);
103             if(cutY > s.val)
104                 updata(s,a,b+1,c,d);
105  
106         }
107     }
108     return s.val;
109 }
110 int main()
111 {
112 //    freopen("C:\\Users\\hyacinthLJP\\Desktop\\in&&out\\contest","r",stdin);
113  
114     scanf("%d%d",&n,&m);
115     for(int i=1;i <= n;++i)
116         scanf("%s",a[i]+1);
117  
118     printf("%d\n",Solve());
119  
120     return 0;
121 }
View Code

 

posted @ 2019-07-20 19:48  HHHyacinth  阅读(402)  评论(0)  编辑  收藏  举报